Vyhledvn vzor template matching Vyhledvn vzor template matching











![Metriky založené na korelaci – 2 D logaritmické hledání • uvažujme čtverec [-p, p]×[-p, Metriky založené na korelaci – 2 D logaritmické hledání • uvažujme čtverec [-p, p]×[-p,](https://slidetodoc.com/presentation_image_h/0e8a8bebd2ac2965cf07f7a70a4135a2/image-14.jpg)


- Slides: 16

Vyhledávání vzorů (template matching)

Vyhledávání vzorů (template matching) • obsah – metriky založené na metodách hledání optimální cesty – metriky založené na korelaci

Párování vzorů (template matching) • doposud: – zatím jsme se snažili přiřadit neznámý vzor do jedné ze znáných tříd • nyní: – vstup: • množina předdefinovaných vzorů. . . šablona/template • neznámý vzor – výstup • máme zjistit, ke které šabloně bude nejlépe „pasovat“ neznámý vzor • šablony – objekty ve scéně, řetězce, slova v mluveném textu, . . • aplikace – rozpoznávání řeči, získávání dat z databáze obrázků, . . • postup – Krok 1 – definování míry podobnosti mezi šablonou a neznámým vzorem – Krok 2 – párování vzorů na šablonu

Metriky založené na metodách hledání optimální cesty • vstup: – vzory jsou řetězce symbolů • výstup: – rozhodnout, který „známý“ řetězec (šablona) nejlépe „pasuje“ na „neznámý“ řetězec • značení: – „známý“ vzor (šablona) r(i) i=1, . . . , I – „neznámý“ vzor t(j) j=1, . . . , J – obecně je I ≠ J • vytvoříme 2 D mřížku – prvky vzorů naneseme na na souřadnicové osy – každý bod mřížky udává vztah mezi příslušným prvkem šablony a neznámého vzoru • př. bod (3, 2) udává vztah mezi r(3) a t(2) neznámý vzor šablona

Metriky založené na metodách hledání optimální cesty • pro každý uzel (i, j) mřížky je definována „vzdálenost“ d(i, j) – vzdálenost mezi elementy r(i) a t(j) • d(i, j|k, l). . . vzdálenost v bodě (i, j) mřížky závisí na bodu (k, l), odkud jsme přišli do bodu (i, j) • délka cesty – součet vzdálenosti uzlů na této cestě • vzdálenost řetězců r a t – délka minimální cesty z (0, 0) do (I, J) • spojení k nalezení cesty s minimální délkou lze použít Bellmanův princip optimality a dynamické programování – Belmannův princip – dynamické programování

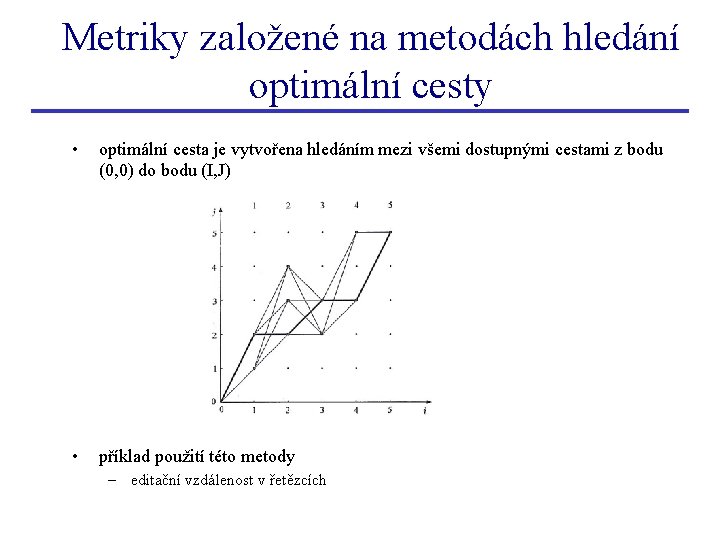
Metriky založené na metodách hledání optimální cesty • optimální cesta je vytvořena hledáním mezi všemi dostupnými cestami z bodu (0, 0) do bodu (I, J) • příklad použití této metody – editační vzdálenost v řetězcích

Metriky založené na korelaci • vstup: – množina známých vzorů – blok dat • výstup: – zjistit, zda se v bloku dat vyskytuje nějaký známý vzor a kde • příklad: analýza scény šedotónový pixel v čase t – součástí tohoto problému je i kódování videa • kódování videa potřebuje odhadnout pohyb ve scéně • tedy hledání stejných objektů, které se pohybují – 1. hledání odpovídajících si pixelů odpovídající pixel na posunuté pozici v čase t-1 • hledáme stejné objekty, které změní pozici v jednotlivých obrazech snímaných s časovým odstupem – 2. odstranění pohybu ze snímků • vytvoříme „rozdílový“ obraz e(i, j, t) = r(i, j, t) - r(i-m, j-n, t-1) • kódujeme jen novou informaci, která je obsažena v nejnovějším snímku (bez redundancí)

Metriky založené na korelaci • vstup: – referenční vzor r(i, j) . . . známý vzor/šablona • matice velikosti M×N – obrazová matice t(i, j). . . neznámý blok dat • matice velikosti I×J – obrazová matice je větší než hledaný referenční vzor • cíl: – najít metriku, která v obrazové matici t(i, j) najde submatici velikosti M×N, která najlépe „pasuje“ na referenční vzor r(i, j) • postup: – referenční vzor postupně přikládáme do všech možných poloh (m, n) obrazové matice – pro každou polohu (m, n) spočteme chybu mezi referenčním vzorem r(i, j) a submaticí z t(i, j)

Metriky založené na korelaci • chyba D pro polohu (m, n): => hledáme takovou polohu (m, n), kde je D(m, n) minimální • vztah pro chybu D(m, n) upravíme: (*) pro daný referenční vzor je konstantní

Metriky založené na korelaci • pokud se výraz (*) v obrazové matici t(i, j) příliš nemění – tj. není velký rozptyl úrovní šedi v testovaném obraze – definujeme korelaci c(m, n) mezi r(i, j) a t(i, j) jako: => minimum D(m, n) je dosaženo, když korelace c(m, n) je maximální • pokud je velký rozptyl úrovní šedi v obrazové matici – korelaci definujeme jako => minimum D(m, n) je dosaženo, když korelace c. N(m, n) je maximální

Metriky založené na korelaci • použijeme Cauchy–Schwarzovu nerovnost • z ní dostaneme => tedy c. N(m, n) ≤ 1 a svého maxima (hodnota 1) dosáhne, když testovaný podobraz je stejný jako referenční vzor

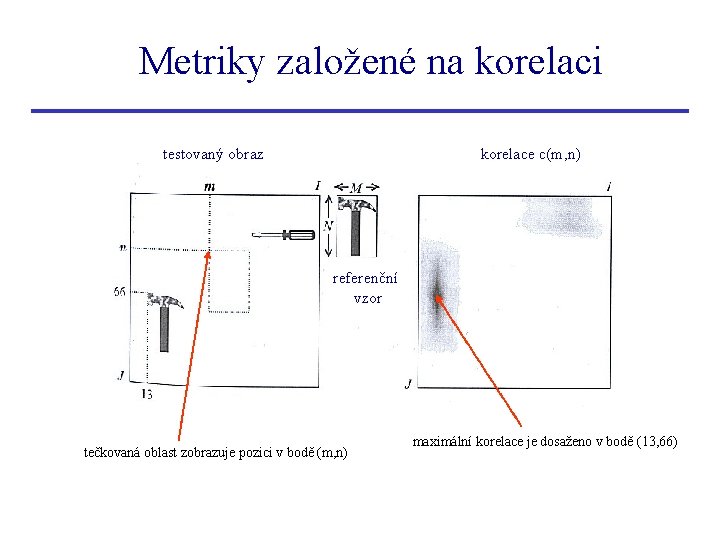
Metriky založené na korelaci testovaný obraz korelace c(m, n) referenční vzor tečkovaná oblast zobrazuje pozici v bodě (m, n) maximální korelace je dosaženo v bodě (13, 66)

Metriky založené na korelaci • zatím jsme uvažovali, že referenční vzory jsou jen posunuty – žádné škálování či rotace – pokud bychom chtěli uvažovat i škálování nebo rotaci: • popsat referenční vzor a testovaný podobraz pomocí momentů, které jsou invariantní vůči daným operacím, a pak spočítat korelaci • použít Fourierovu nebo Mellinovu transformaci • hledání správné polohy v t(i, j), kde je dosaženo max. korelace – početně nejnáročnější operace – typicky hledáme správné polohy ve čtverci [-p, p]×[-p, p] vycentrované v bodě (x, y) obrazu t(i, j) => obecně potřebujeme (2 p+1)2 MN operací sčítání a násobení – v praxi se používají heuristiky na hledání nejlepší pozice • nemusí nalézt maximum (–) • sníží počet operací (+)
![Metriky založené na korelaci 2 D logaritmické hledání uvažujme čtverec p pp Metriky založené na korelaci – 2 D logaritmické hledání • uvažujme čtverec [-p, p]×[-p,](https://slidetodoc.com/presentation_image_h/0e8a8bebd2ac2965cf07f7a70a4135a2/image-14.jpg)
Metriky založené na korelaci – 2 D logaritmické hledání • uvažujme čtverec [-p, p]×[-p, p] kde p = 7 • střed čtverce je bod (0, 0) • nejprve spočteme korelaci ve středu a v 8 bodech na obvodu čtverce [-p/2, p/2] × [-p/2, p/2] (žluté body) vzdálenost mezi žlutými body je • • • nechť největší korelace je v bodě (-4, 0) (oranžový čtverec) tento bod se stane středem čtverce pro další iteraci

Metriky založené na korelaci – 2 D logaritmické hledání • • • v další iteraci pracujeme se čtvercem se středem (-4, 0) a velikosti [-p/4, p/4]×[-p/4, p/4] spočteme korelaci v 8 bodech na obvodu čtverce (modré body) vzdálenost mezi modrými body je proces opakujeme až 8 bodů bude na obvodu čtverce o velikosti [-1, 1]×[-1, 1], který má střed v předchozím optimálním bodě (zelený čtverec a fialové kolečko) červený bod je bod s maximální korelací a výpočet končí počet operací je MN(8 k+1)

Metriky založené na korelaci – sekvenční metoda • heuristika vychází přímo z definice chyby D(m, n) mezi referenčním vzorem a podobrazem • definujeme chybu na okénku – tedy chyba se počítá na malém okénku p, q = 1, 2, . . . (kde p ≤ M, q ≤ N) • výpočet Dpq(m, n) skončí, když chyba je větší než předdefinovaná prahová hodnota – a pak se posuneme do jiné polohy (m, n) a zopakujeme výpočet
 Visual pathway psychology
Visual pathway psychology Pengertian pola digital
Pengertian pola digital Bolongie
Bolongie Matching template for quiz
Matching template for quiz Chamfer matching
Chamfer matching Match statement
Match statement Template matching psicologia
Template matching psicologia Sebutkan fitur fitur yang terdapat di panel publisher
Sebutkan fitur fitur yang terdapat di panel publisher Cie color matching functions table
Cie color matching functions table Strategies for shifting demand to match capacity
Strategies for shifting demand to match capacity Implementing strategies management and operations issues
Implementing strategies management and operations issues Super matching bonus
Super matching bonus Job matching definition
Job matching definition John proctor iii
John proctor iii Simple matching coefficient
Simple matching coefficient Histogram matching
Histogram matching String matching
String matching