VY32INOVACE 22 18 Geometrick posloupnost 3 st Opakovn

VY_32_INOVACE_ 22 -18 Geometrická posloupnost (3. část)

Opakování základních poznatků o geometrické posloupnosti: § Kdy je posloupnost geometrická? § Jak dokazujeme, že daná posloupnost je geometrická? § Jaké jsou vztahy mezi jednotlivými členy geometrické posloupnosti? § Jak vypočítáme součet prvních n členů geometrické posloupnosti?

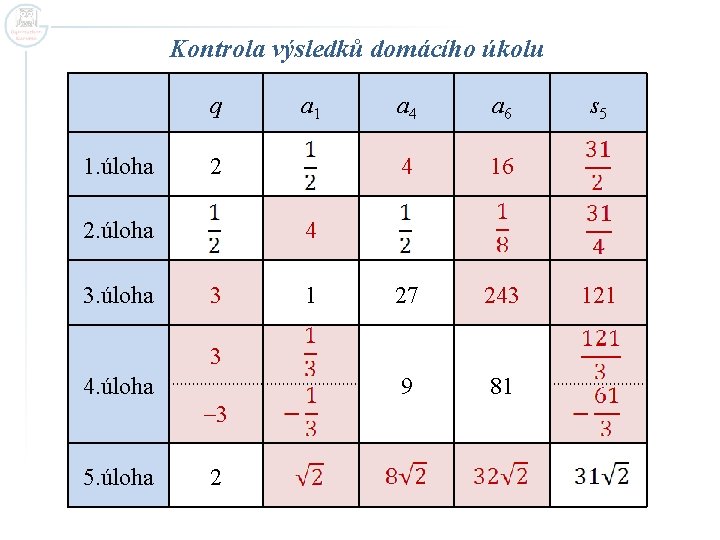
Kontrola výsledků domácího úkolu q 1. úloha 2 2. úloha 3. úloha a 1 a 4 a 6 4 16 27 243 9 81 4 3 1 3 4. úloha – 3 5. úloha s 5 2 121

Samostatná práce V geometrické posloupnosti platí: a) Určete tuto posloupnost (tj. vypočtěte ). b) Zapište danou posloupnost vzorcem pro n-tý člen. c) Odvoďte vzorec pro součet prvních n členů této posloupnosti.

Kontrola výsledků samostatné práce a) b) c)

Úloha 1 Přičteme-li k číslům stejné číslo, dostaneme první tři členy geometrické posloupnosti. Určeme tuto geometrickou posloupnost.

Řešení úlohy 1 Členy neznámé geometrické posloupnosti označme Potom platí: Protože se jedná o geometrickou posloupnost, je podíl sousedních členů stejný, tzn. , že platí: Odtud pak je . Závěr: Hledaná geometrická posloupnost má .

Úloha 2 Délky hran kvádru tvoří tři po sobě jdoucí členy geometrické posloupnosti. Jejich součet je 26 cm. Jak velký je jeho povrch, je-li objem kvádru 216 cm 3.

Řešení úlohy 2 Hrany kvádru označíme a, b, c a předpokládejme, že Označíme-li, že hrana b = x, pak platí: (q – kvocient geometrické posloupnosti, q > 1) Délky hran: a = 2 cm, b = 6 cm, c = 18 cm. Závěr: Povrch kvádru je 312 cm 2. .

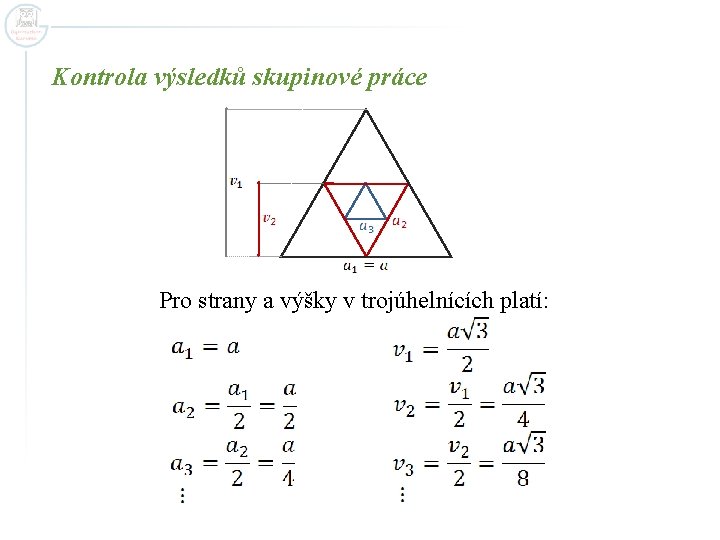
Skupinová práce Spojíme-li středy stran rovnostranného trojúhelníka o straně a, získáme opět rovnostranný trojúhelník. Stejným způsobem pak vznikají další rovnostranné trojúhelníky. Vypočtěte a) obsah šestého trojúhelníka, b) součet obsahů prvních šesti trojúhelníků.

Kontrola výsledků skupinové práce Pro strany a výšky v trojúhelnících platí:

Pro obsahy trojúhelníků platí: geom. posl.

Domácí úloha Délky stran trojúhelníku ABC tvoří geometrickou posloupnost. Vypočtěte jejich velikost, víte-li, že obvod trojúhelníku je 21 cm a prostřední strana má délku 6 cm.

Děkuji za pozornost. Autor DUM: RNDr. Ivana Janů Autor příkladů a obrázků: RNDr. Ivana Janů