VY32INOVACE 22 15 Geometrick posloupnost 1 st loha

VY_32_INOVACE_ 22 -15 Geometrická posloupnost (1. část)

Úloha 1 a) Sestrojme grafy následujících posloupností zadaných výčtem jejich prvků: b) Jak se liší u těchto posloupností člen následující od členu předchozího? c) Zapišme tyto posloupnosti rekurentně. d) Sestavme vzorec pro n–tý člen daných posloupností. e) Jedná se v těchto případech o funkci? O jakou?

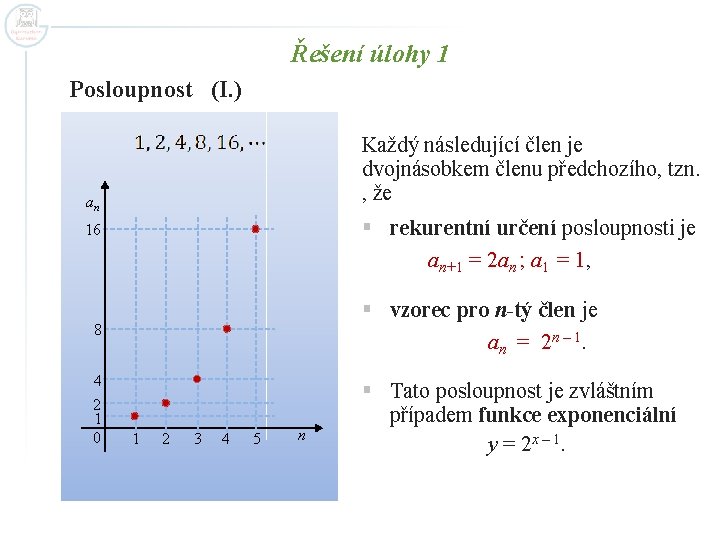
Řešení úlohy 1 Posloupnost (I. ) Každý následující člen je dvojnásobkem členu předchozího, tzn. , že an § rekurentní určení posloupnosti je an+1 = 2 an ; a 1 = 1, 16 § vzorec pro n-tý člen je an = 2 n – 1. 8 4 2 1 0 1 2 3 4 5 n § Tato posloupnost je zvláštním případem funkce exponenciální y = 2 x – 1.

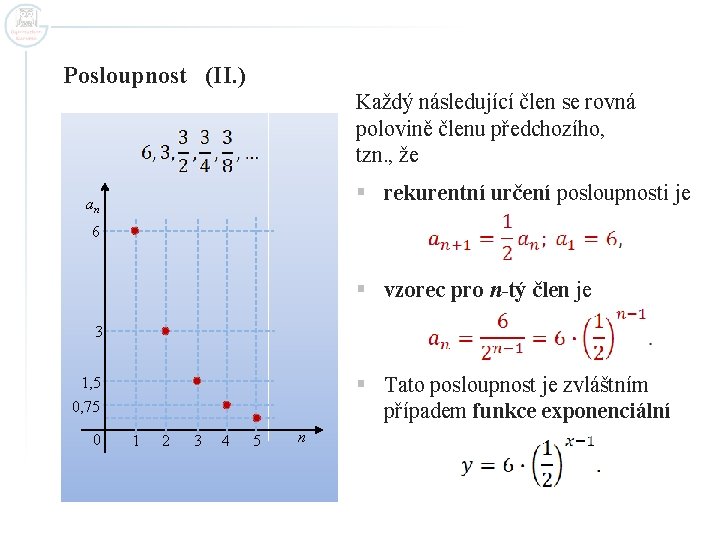
Posloupnost (II. ) Každý následující člen se rovná polovině členu předchozího, tzn. , že § rekurentní určení posloupnosti je an 6 § vzorec pro n-tý člen je 3 § Tato posloupnost je zvláštním případem funkce exponenciální 1, 5 0, 75 0 1 2 3 4 5 n

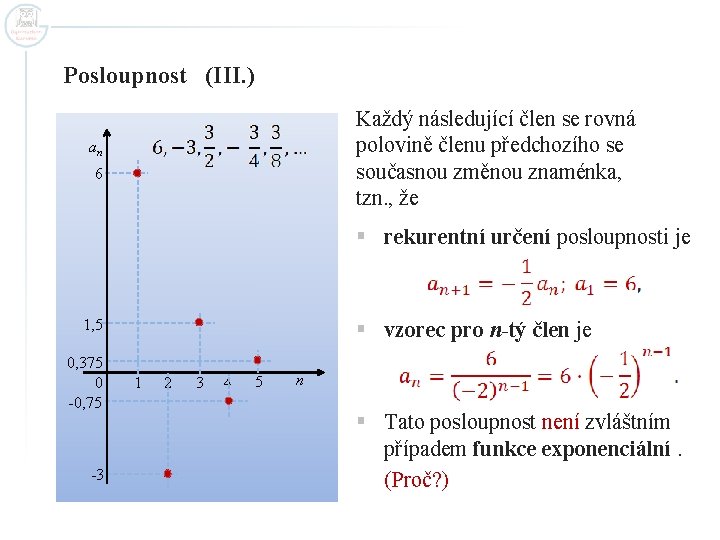
Posloupnost (III. ) Každý následující člen se rovná polovině členu předchozího se současnou změnou znaménka, tzn. , že an 6 § rekurentní určení posloupnosti je 1, 5 0, 375 0 -0, 75 -3 § vzorec pro n-tý člen je 1 2 3 4 5 n § Tato posloupnost není zvláštním případem funkce exponenciální. (Proč? )

Definice geometrické posloupnosti Posloupnost se nazývá geometrická, právě když existuje takové reálné číslo q, že Reálné číslo q je tzv. kvocient geometrické posloupnosti. Poznámka: Ve všech úlohách budeme předpokládat, že a 1 0 a zároveň q 0.

Vlastnosti geometrické posloupnosti: 1. V geometrické posloupnosti je vždy podíl dvou libovolných sousedních členů konstantní, protože . 2. Jestliže kvocient , jedná se o zvláštní případ exponenciální funkce, grafem jsou body ležící na exponenciále. 3. Omezení posloupnosti a její monotónnost záleží na hodnotách a.

Odpovězte na zadané otázky v následujícím testu. Návod: Využijte grafů posloupností. (Časový rozsah celého testu jsou 3 minuty. ) (Test ve formátu *. ppt nebo *. pdf )

Úloha 2 Která z následujících posloupností je geometrická? Dokažme toto tvrzení na základě definice geometrické posloupnosti: a) b) c)

Řešení úlohy 2 Má-li být posloupnost geometrická, musí platit, že podíl jejich sousedních členů je konstantní a rovná se kvocientu q. a) b) c) Závěr: O geometrickou posloupnost se jedná pouze v a), c).

Domácí úkol § Která z následujících posloupností je aritmetická a která geometrická? § Dokažte tato tvrzení na základě definice aritmetické a geometrické posloupnosti. § Obě posloupnosti zapište rekurentně. a) b)

Děkuji za pozornost. Autor DUM: RNDr. Ivana Janů Autor příkladů a grafů: RNDr. Ivana Janů