VY32INOVACE 22 04 Posloupnosti a jejich vlastnosti 3

VY_32_INOVACE_ 22 -04 Posloupnosti a jejich vlastnosti (3. část)

Opakování základních poznatků § Co je to posloupnost? § Jakými matematickými vztahy můžeme zadat posloupnost? § Jak lze zapsat posloupnost všech sudých (lichých) přirozených čísel • vzorcem pro n-tý člen, • rekurentně?

Kontrola výsledků domácího úkolu 1. Posloupnost je dána rekurentně vzorcem její první člen je kořenem rovnice , . Určete prvních pět členů této posloupnosti. Řešení: Kořen rovnice je . Závěr: Prvních pět členů posloupnosti jsou čísla 5, 5, 10, 30, 120.

2. Posloupnost je dána rekurentně vzorcem členy jsou kořeny rovnice Určete prvních pět členů této posloupnosti. Řešení: Kořeny rovnice jsou Závěr: Prvních pět členů posloupnosti jsou čísla 1, 3, 0, – 2, 1.

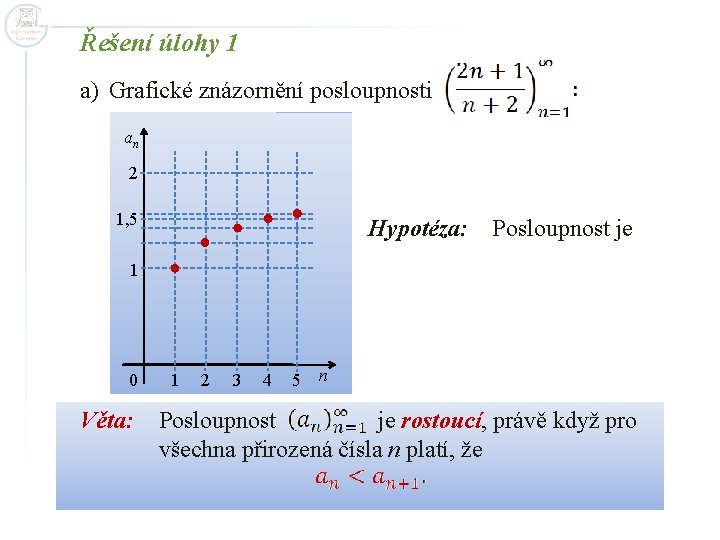
Vlastnosti posloupností Monotónnost posloupnosti Úloha 1 Znázorněme graficky několik prvních členů posloupnosti , jestliže a) b) Stanovme hypotézy, zda jsou tyto posloupnosti rostoucí či klesající. Hypotézy dokažme a vyslovme platný závěr o monotónnosti daných posloupností.

Řešení úlohy 1 a) Grafické znázornění posloupnosti an 2 1, 5 1 0 Věta: Hypotéza: Posloupnost je rostoucí. 1 2 3 4 5 n Posloupnost je rostoucí, právě když pro všechna přirozená čísla n platí, že

Důkaz: Má-li být posloupnost rostoucí, musí platit, že Nejprve vytvoříme člen an + 1: Pak platí, že Úpravou této nerovnice jsme dostali pravdivý výrok, tzn. , že hypotéza platí. Závěr: Posloupnost je rostoucí.

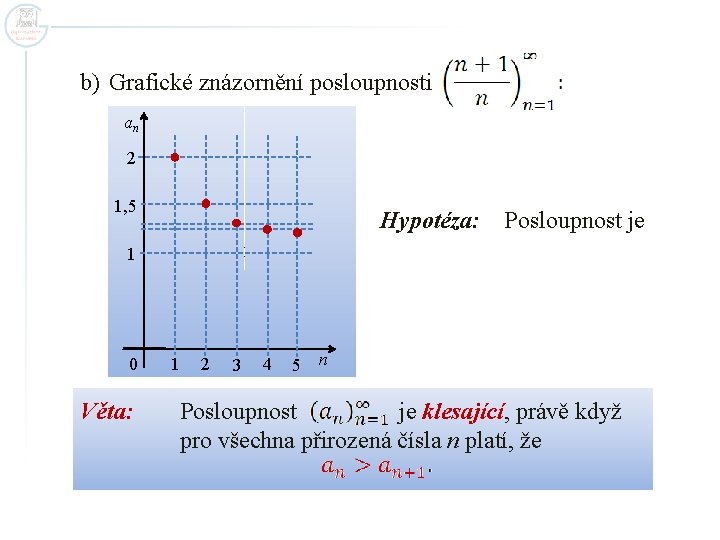
b) Grafické znázornění posloupnosti an 2 1, 5 Hypotéza: klesající. 1 0 Věta: Posloupnost je 1 2 3 4 5 n Posloupnost je klesající, právě když pro všechna přirozená čísla n platí, že

Důkaz: Máme dokázat, že Vytvoříme člen Pak platí, že Úpravou této nerovnice jsme dostali pravdivý výrok. Závěr: Posloupnost je klesající.

Úloha 2 Pro která reálná čísla x je posloupnost a) rostoucí, b) klesající?

Řešení úlohy 2 a) Má-li být posloupnost rostoucí, pak platí: Závěr: b) Posloupnost je rostoucí pro všechna kladná Pro klesající posloupnost je výpočet analogický. Závěr: Posloupnost je klesající pro všechna záporná čísla x.

Samostatná práce Zjistěte a dokažte, zdá daná posloupnost je rostoucí či klesající: a) b)

Kontrola výsledků samostatné práce a) Klesající, protože platí : (výrok pravdivý) b) Rostoucí, protože platí : (výrok pravdivý)

Domácí úkol Pro která reálná čísla x je posloupnost a) rostoucí, b) klesající?

Děkuji za pozornost. Autor DUM: RNDr. Ivana Janů Autor příkladů a grafů: RNDr. Ivana Janů