Vortex configuration of bosons in an optical lattice

Vortex configuration of bosons in an optical lattice Congjun Wu Kavli Institute for Theoretical Physics, UCSB Collaborators: H. D. Chen, J. P. Hu, S. C. Zhang Ref: Phys. Rev. A 69, 43609 (2004). Boulder Summer School, July, 2004 1
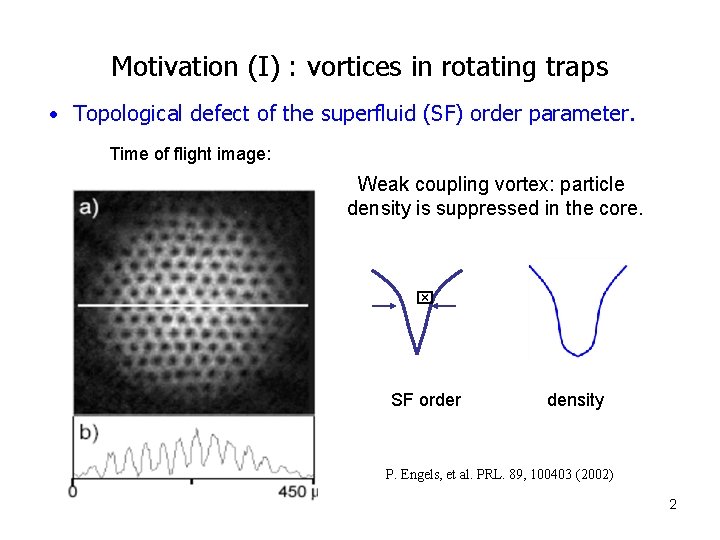
Motivation (I) : vortices in rotating traps • Topological defect of the superfluid (SF) order parameter. Time of flight image: Weak coupling vortex: particle density is suppressed in the core. x SF order density P. Engels, et al. PRL. 89, 100403 (2002) 2

Motivation (II) : SF- Mott-Insulator transition Superfluid Mott insulator M. Greiner et al. , Nature (London) 415, 39 (2002). • How about the vortex near the SF-Mott insulator (MI) transition? 3
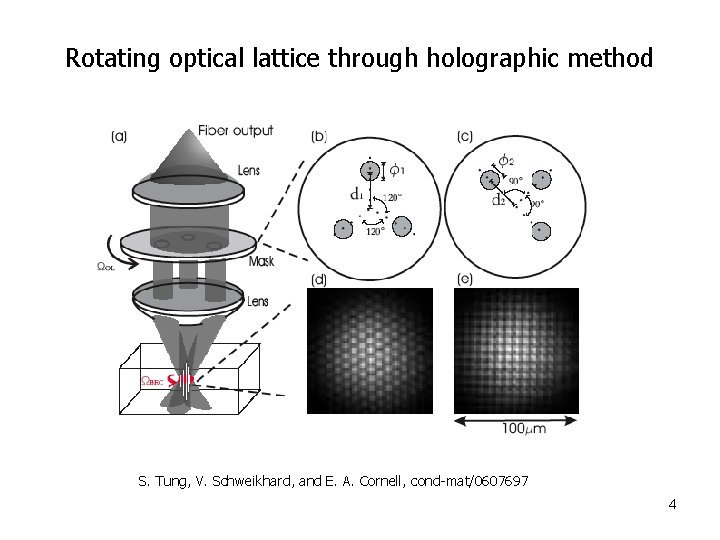
Rotating optical lattice through holographic method S. Tung, V. Schweikhard, and E. A. Cornell, cond-mat/0607697 4
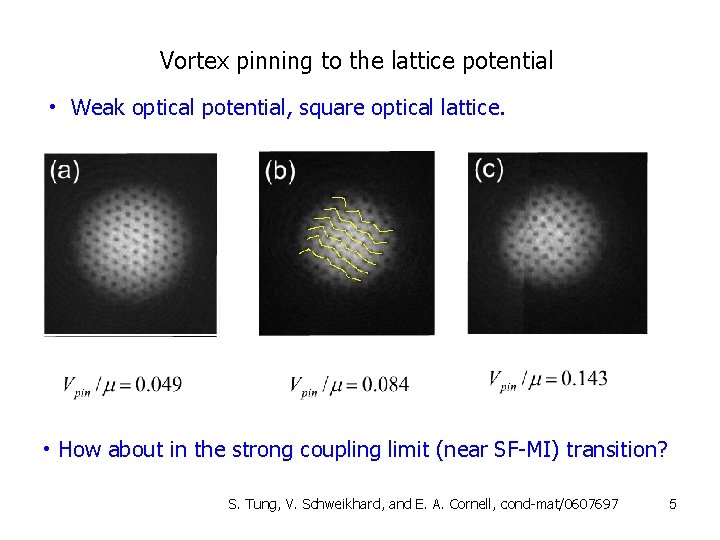
Vortex pinning to the lattice potential • Weak optical potential, square optical lattice. • How about in the strong coupling limit (near SF-MI) transition? S. Tung, V. Schweikhard, and E. A. Cornell, cond-mat/0607697 5
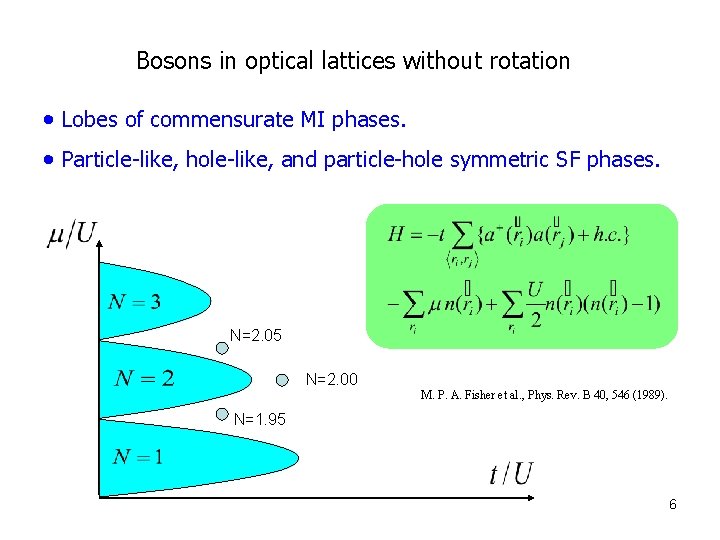
Bosons in optical lattices without rotation • Lobes of commensurate MI phases. • Particle-like, hole-like, and particle-hole symmetric SF phases. N=2. 05 N=2. 00 M. P. A. Fisher et al. , Phys. Rev. B 40, 546 (1989). N=1. 95 6

Superfluid vortex with nearly Mott-insulating core • Hole-like vortex (t/U=0. 02) • particle-like vortex <N>=1. 95 (t/U=0. 02) <N>=2. 05 C. Wu , et al. , Phys. Rev. A, 69, 43609 (2004); cond-mat/0211457. 7

Bosons in rotating optical lattices • Vector potential for Coriolis force : l Neglect the trapping potential and the centrifugal potential. Josephson junction array in the magnetic field at low temperatures. l 8

Mean field approximation: Guzwiller • Decouple to single site problems: • The MF ground state wavefunction: • The spatially dependent SF order: • Valid at the small t/U. 9
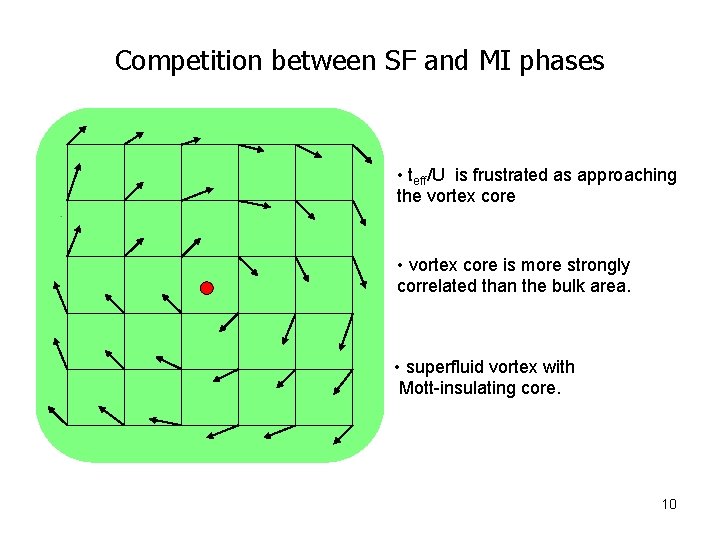
Competition between SF and MI phases • teff/U is frustrated as approaching the vortex core • vortex core is more strongly correlated than the bulk area. • superfluid vortex with Mott-insulating core. 10
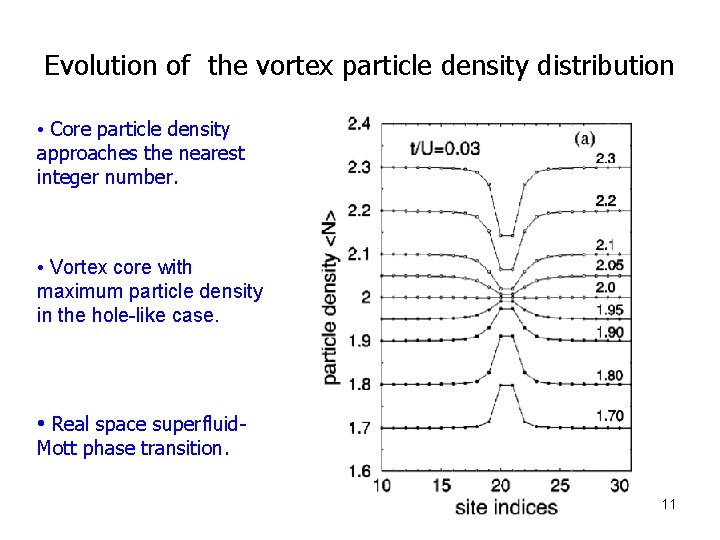
Evolution of the vortex particle density distribution • Core particle density approaches the nearest integer number. • Vortex core with maximum particle density in the hole-like case. • Real space superfluid. Mott phase transition. 11
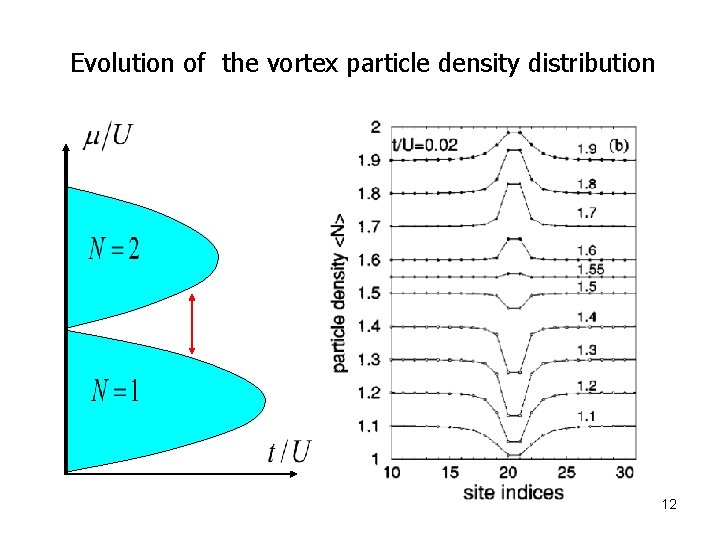
Evolution of the vortex particle density distribution 12
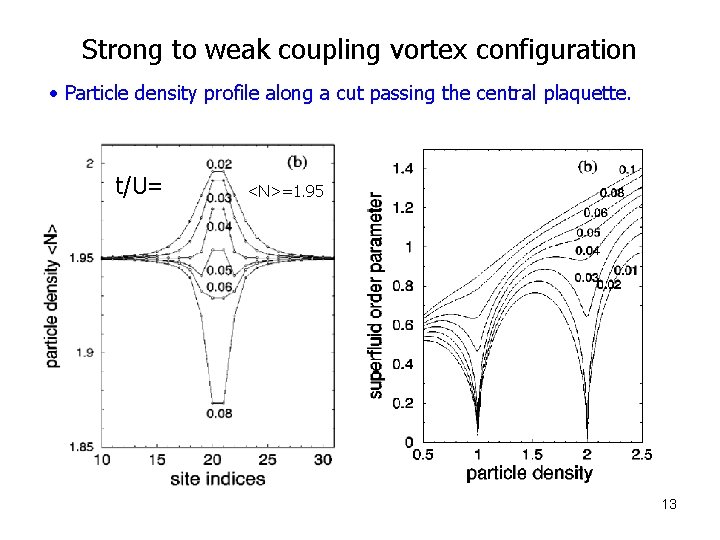
Strong to weak coupling vortex configuration • Particle density profile along a cut passing the central plaquette. t/U= <N>=1. 95 13
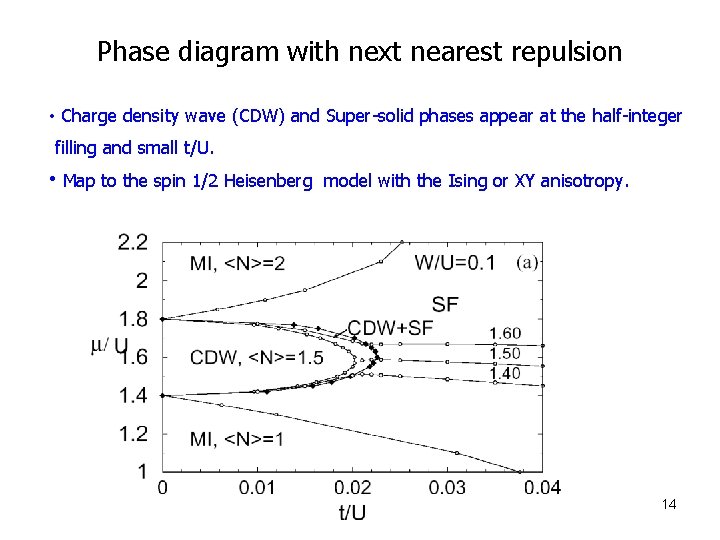
Phase diagram with next nearest repulsion • Charge density wave (CDW) and Super-solid phases appear at the half-integer filling and small t/U. • Map to the spin 1/2 Heisenberg model with the Ising or XY anisotropy. 14
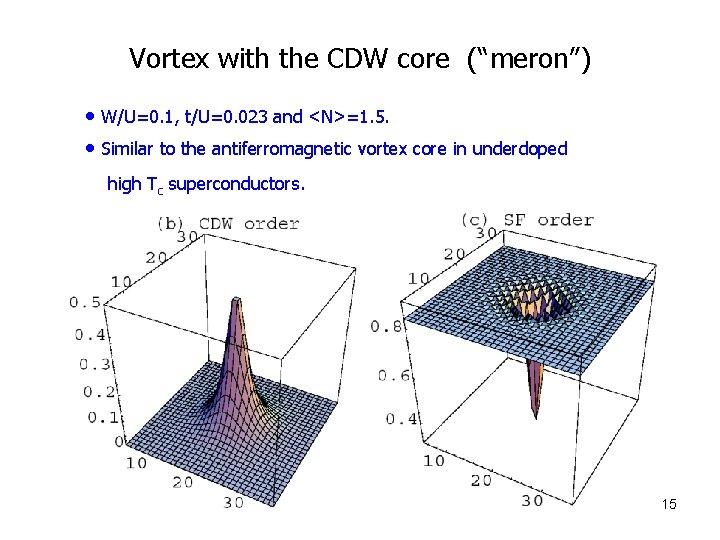
Vortex with the CDW core (“meron”) • W/U=0. 1, t/U=0. 023 and <N>=1. 5. • Similar to the antiferromagnetic vortex core in underdoped high Tc superconductors. 15

Possible experiments • Vortex core size on the optical lattice is about 2 microns. Focus the probe laser beam to this size and scan the lattice to determine the particle density distribution. • Raman photon-association to detect the percentage of Mott region. (D. J. Heinzen’s group) • The Josephson junction array system in the magnetic field. From the electrical field distribution, it is possible to determine the vortex charge. 16

Summary • The vortex core is a more strongly coupled region compared to the bulk area. • Near the SF-MI transition, the vortex core is nearly Mott insulating and the core particle density approaches the nearest commensurate value. • As t/U increases, the vortex evolves from the strong coupling configuration to weak coupling one. 17
- Slides: 17