Vorstellen und Herleiten der Horner Schemas Um den

Vorstellen und Herleiten der Horner Schemas Um den Graph einer Funktion, wie z. B. f(x)= 2 x³ -5 x² -6 x +9 zu erstellen, kann man eine Wertetabelle anlegen. Dabei werden verschiedene Werte für x in die Funktion eingesetzt, und man erhält entsprechende f(x)-Werte.

Beispiel: f(x)= 2 x³ -5 x² -6 x +9 Werte-Tabelle: x f(x) 0 9 1 0 x 1= 0 f(0) = 2(0)³ -5(0)² -6(0) +9 f(0) = 9 x 2= 1 f(1) = 2(1)³ -5(1)² -6(1) +9 f(1) = 2· 1· 1· 1 -5· 1· 1 -6· 1 +9 f(1) = 2 f(1) = 0 usw. . -5 -6 +9

Schauen wir uns einmal an, was dabei genau passiert: Wenn wir z. B. x=2 in f(x) einsetzen, rechnen wir: f(2) = 2(2)³ -5(2)² -6(2) +9 = 2· 2· 2· 2 · · · --5· 2· 2 · · --6· 2 · ++9 Das könnt ihr ja mal grad im Kopf machen! das sind 6 Multiplikationen und 3 Additionen und wir erhalten als Ergebnis = 16 – 20 -12 +9 = -7

Der britische Mathematiker William George Horner, kam auf eine Idee, wie man diesen Rechenvorgang vereinfachen kann. (Er hatte noch keinen Taschenrechner ; )) Er dachte sich folgendes: Die Funktion: f(x)= 2 x³ -5 x² -6 x +9 Ist ja: f(x)= 2·x·x·x x -5·x·xx -6·xx +9 Daraus folgt: Man sieht: f(x)= x·(2·x·x -5·x -6) +9 Und weiter: Die ersten drei Terme enthalten alle mindestens ein x! f(x)= x·(2·x·x -5·x -6) +9 Daher kann man dieses x ausklammern! f(x)= x·(x·(2·x +9 · · · --5) --6) + Dadurch erhält man: 3 Multis und 3 Addis Insgesamt spart man also 3 Multis ein!

Der Clou kommt aber erst noch ; ) Horner hat noch konsequenter weitergedacht und die Rechnung in einfaches Rechenschema verwandelt: Die umgeformte Funktion f(x)= x·(x·(2·x -5) -6) +9 rechnet man ja von innen nach außen, also z. B. für x=2: Erhält man: und rechnet f(2)= 2·(2·(2· 2 -5) -6) +9 ((2·( -8 -5 ) +9 -7 -16 +9 ( 2· 2 = 2· 2·(2·(2· 2 -5))-6) -16 4 -2 -1 noch einmal zum mitdenken ; )

Die gegebene Funktion f(x) = formt man durch ausklammern von x um in: f(x)= x·(x·(2·x -5) -6) +9 Für x=2 erhält man dann: f(2)= 2·(2·(2· 2 -5) -6) +9 Und rechnet: 2 x³ -5 x² -6 x +9 ((2·( -8 -5 ) +9 -7 -16 +9 ( 2· 2 = 2· 2·(2·(2· 2 -5))-6) -16 4 -2 -1 Also Multi mit x=2 , also Addi also Multi mit x=2 , also Addi Diesen Rechengang hat Horner nun in einfaches Rechenschema gebracht. Das sogenannte: Horner Schema

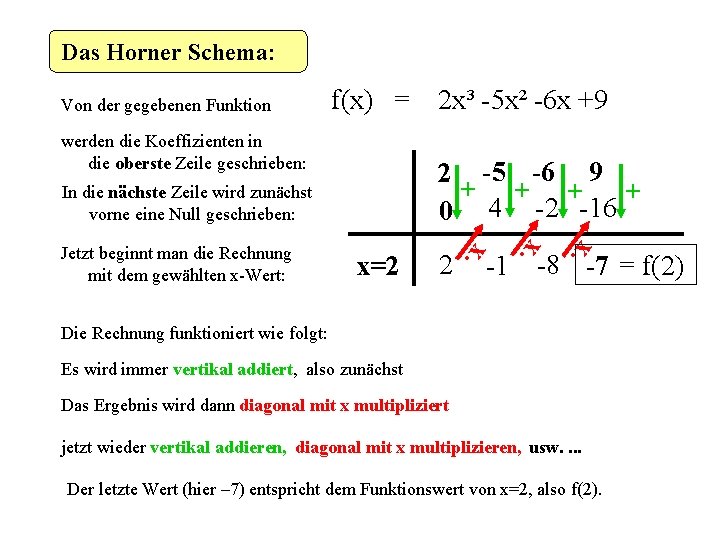
Das Horner Schema: f(x) = werden die Koeffizienten in die oberste Zeile geschrieben: 2 ·x x=2 ·x 2 -5 -6 9 + + 0 4 -2 -16 In die nächste Zeile wird zunächst vorne eine Null geschrieben: Jetzt beginnt man die Rechnung mit dem gewählten x-Wert: 2 x³ -5 x² -6 x +9 ·x Von der gegebenen Funktion -1 -8 -7 = f(2) Die Rechnung funktioniert wie folgt: Es wird immer vertikal addiert, also zunächst Das Ergebnis wird dann diagonal mit x multipliziert jetzt wieder vertikal addieren, diagonal mit x multiplizieren, usw. . Der letzte Wert (hier – 7) entspricht dem Funktionswert von x=2, also f(2).

Arbeitsauftrag: Die Funktion f(x) = 2 x³ -5 x² -6 x +9 hat eine Nullstelle bei x 1=1 a) Führen Sie bitte eine Polynomdivision von f(x) und dem Linearfaktor (x-1) durch. b) Führen Sie bitte das Horner Schema mit f(x) und dem x-Wert x 1=1 durch. c) Was fällt Ihnen auf, wenn Sie die Ergebnisse vergleichen?

Erkenntnis: Wenn bei einem Rechendurchlauf des Horner Schemas das Endergebnis (der f(x)-Wert) gleich Null ist, so entsprechen die übrigen Zahlen der Ergebniszeile den geordneten Koeffizienten der Restfunktion! Beispiel: f(x) = 2 x³ -5 x² -6 x +9 Horner Schema x=1 2 0 -5 -6 9 2 -3 -9 0 = f(1) =Restfunktion f. Rest(x)= 2 x² -3 x -9 = 0 weiter mit p/q-Formel

Zusammenfassung: Wenn man die Nullstellen von Funktionen dritter und höherer Ordnung bestimmen möchte, ist folgendes Vorgehen sinnvoll: Beispiel: 1) 1. Nullstelle raten: f(x) = 2 x³ -5 x² -6 x +9 x 1=1 f(1) =0 zweiten Schritt kann man sich nun entscheiden, man 2 a)Als Polynomdivision oder 2 b) Horner ob Schema Polynomdivision oder das Horner Schema nutzen möchte: (2 x³ -5 x² -6 x +9): (x-1)= 2 x² -3 x -9 -(2 x³-2 x²) -3 x² -6 x f. Rest(x) -(3 x² +3 x) -9 x +9 -(9 x +9) 0 2 -5 -6 9 0 2 -3 -9 = x=1 2 -3 -9 0 = f(1) f. Rest(x)= 2 x² -3 x -9 3) Die beiden weiteren Nullstellen mit der Restfunktion f. Rest(x) z. B. mittels p/q-Formel berechnen. 4) Alle Nullstellen N 1(x 1/0) , N 2(x 2/0) , N 3(x 3/0) hinschreiben.