Voronoi diagrams of nice point sets Nina Amenta

Voronoi diagrams of “nice” point sets Nina Amenta UC Davis “The World a Jigsaw”

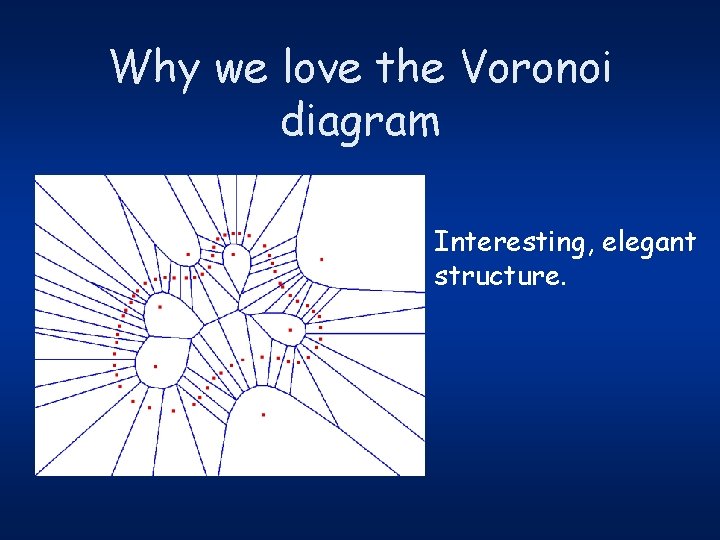
Why we love the Voronoi diagram Interesting, elegant structure.

Why we love the Voronoi diagram It’s useful! for surface reconstruction. . input output

Point Set Capture Point Grey Bumblebee Cyberware Boom in surface reconstruction research.

Why we love the Voronoi diagram. . . and for mesh generation. Jonathan Shewchuk, “triangle” Triangles with no small angles, respect size of input features.

Why we love the Voronoi diagram Shewchuk, ‘ 98 Three-dimensional tetrahedralization

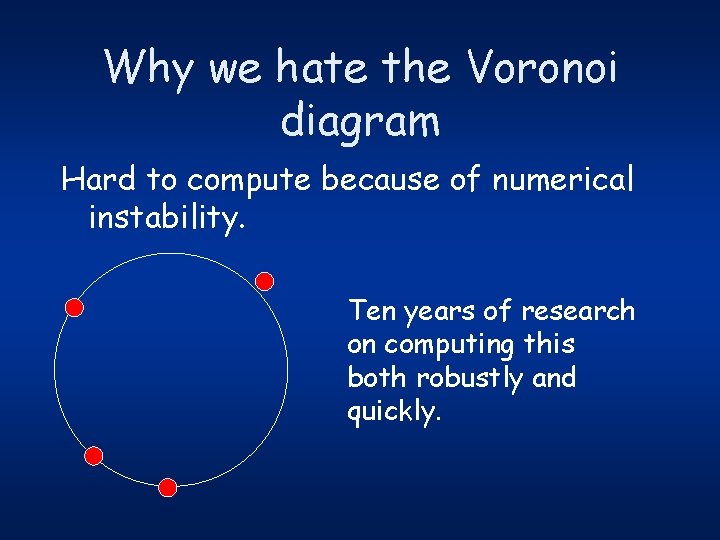
Why we hate the Voronoi diagram Hard to compute because of numerical instability. Ten years of research on computing this both robustly and quickly.

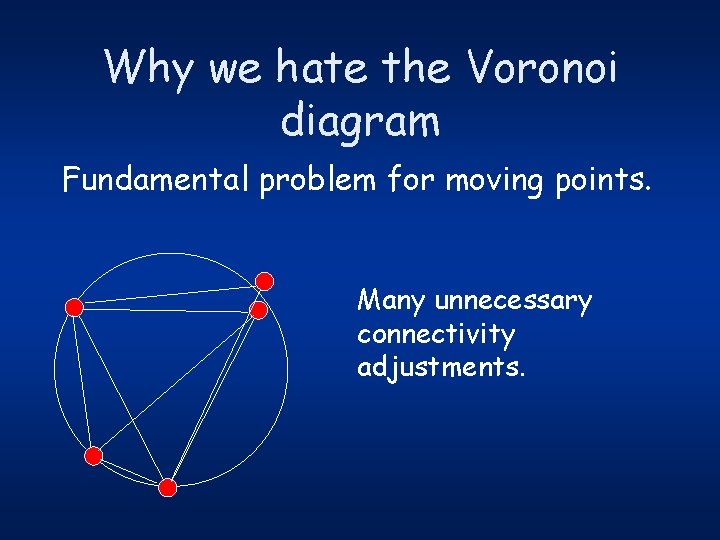
Why we hate the Voronoi diagram Fundamental problem for moving points. Many unnecessary connectivity adjustments.

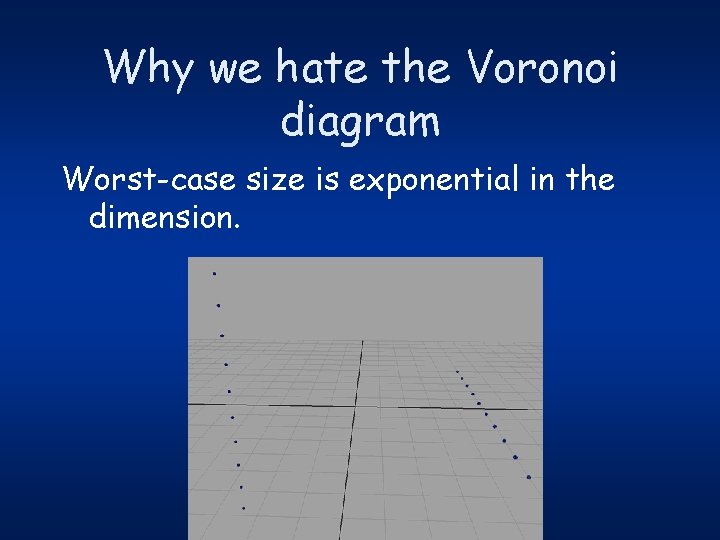
Why we hate the Voronoi diagram Worst-case size is exponential in the dimension. O( n[d/2] )

Why we hate the Voronoi diagram Worst-case size is exponential in the dimension.

Why we hate the Voronoi diagram Dual sliver tetrahedra!

Worst-case approach We have done a great job of designing programs and algorithms which robustly handle all inputs.

Consider nice inputs! Users want to reconstruct surface or mesh object, they don’t care what the point set is.

Surface reconstruction Requires 3 D Delaunay triangulation. O(n 2)? Only if you really, really try. . . these points are not on a 1 D set, they lie on a 2 D surface. Dwyer, 91, uniform random points have O(n)size Delaunay triangulation in any fixed dimension. But what about points on (near) lower dimensional manifolds?

Practice suggests O(n) A & Choi, 01 Adding samples on surfaces in random order, #Del. tetrahedra grows linearly.

Attali & Boissonnat 03 Complexity of Delaunay triangulation is O(n).

Nicely sampled polygons Fixed set of polygons in R 3. Area, boundary length, number of polygons constant.

Sampling model Every point has at least one and at most k samples within distance 1/n 2. Consider behavior as n->infinity. Golin & Na have similar results in random case.

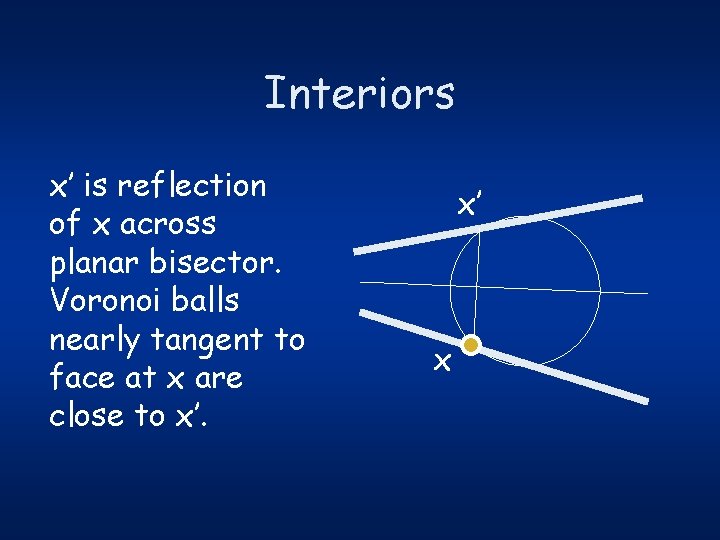
Interiors x’ is reflection of x across planar bisector. Voronoi balls nearly tangent to face at x are close to x’. x’ x

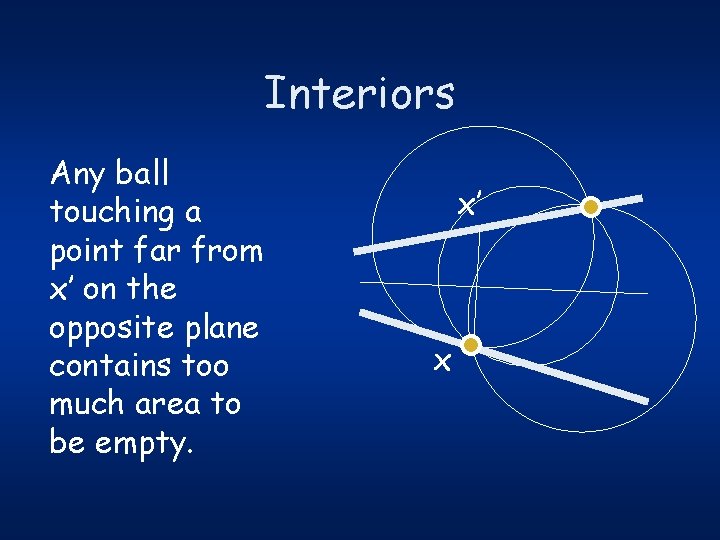
Interiors Any ball touching a point far from x’ on the opposite plane contains too much area to be empty. x’ x

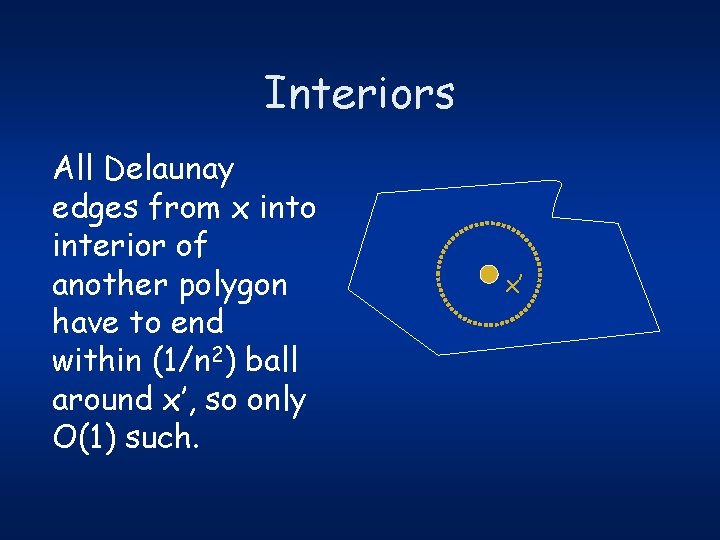
Interiors All Delaunay edges from x into interior of another polygon have to end within (1/n 2) ball around x’, so only O(1) such. x’

Edges Sample near an edge can be connected to more other samples. . but there are only sqrt(n) of them. The difficult part of the proof!

Open Questions • Attali, Boissonnat & Lieuter, 03, “Generic” smooth surface S, O(n log n) - best possible? • Erickson, 01, wickedly chosen smooth surface can be O(n 3/2) • Noise? Higher dimensions? Argument we just did applies to interiors of (d-1)-planes in Rd.

Mesh Generation All triangles approximately equilateral, input features (or given density function) controls maximum size.

Harder in 3 D Have to avoid slivers! Recent approach: Alliez, Cohen-Steiner, Yvinec & Desbrun, Siggraph ‘ 05. Related to. .

Llyod’s method, 1982 Compute Voronoi diagram. Move each sample to the center of mass of its Voronoi cell. Repeat.

Centroidal Voronoi Diagram When density is uniform, converges at a minimum of: ∫x (x - c(x) )2 c(x) = center of Voronoi cell containing x

2 D, uniform distribution modulo edge effects bounded domain

2 D, non-uniform distribution Distribution given by darkness of photo - stippling patterns! Adrian Secord, NPAR 2002

In 3 D, more difficult No proof that converges to closest sphere packing. Hales, ‘ 98, showed closest sphere packing in 3 D is regular. Cannonball packing is not unique - each layer has two alternate translations.

Different iteration Does not seem to work well in practice. Making Voronoi cells round does not necessarily make Delaunay tetrahedra round. Idea (Chen and Xu): Directly optimize Delaunay tetrahedra.

Property to dualize? x -> ( x, ||x||2 ) Convex Hull projects down to Delaunay triangulation Intersection of tangent halfspaces projects down to Voronoi diagram.

Property to dualize? local minimum of: E =∫x (x - c(x) )2 c(x) E = error of Voronoi polytope as approximation of paraboloid.

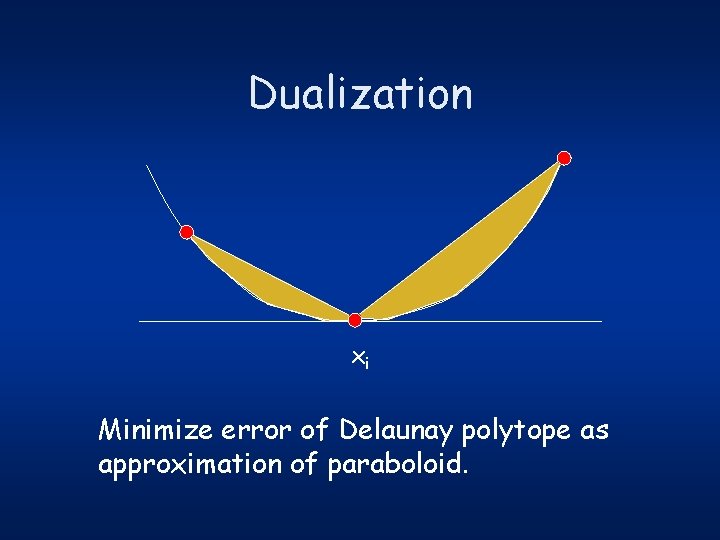
Dualization xi Minimize error of Delaunay polytope as approximation of paraboloid.

Error minimizing iteration x New x = 1/area(region) T (area(T) circumcenter(T) )

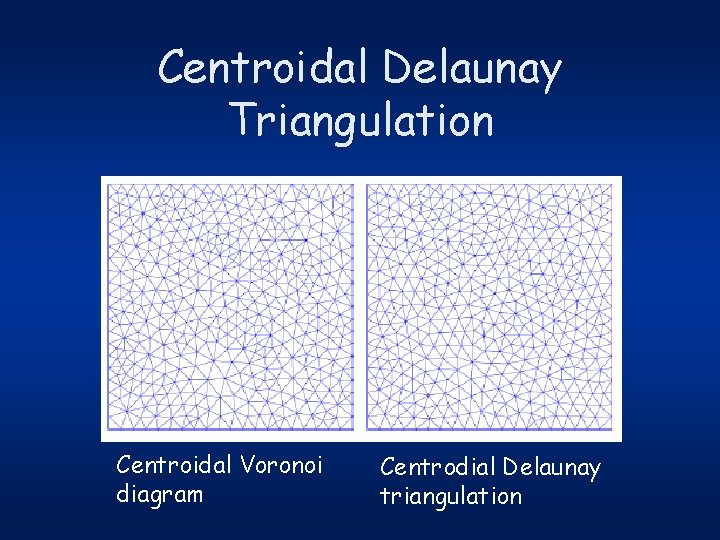
Centroidal Delaunay Triangulation Centroidal Voronoi diagram Centrodial Delaunay triangulation

Good in practice Many open questions in theory. . .

Open Questions • CVD and CDT form sphere packings in 3 D? • Can we compute them without iterating Delaunay triangulation? • Can we compute the DT of a nice distribution using only floating-point arithmetic?

Moving Points • Show that some iterative process maintains a distribution that avoids unnecessary flips (no 5 points near a sphere).

Thank you.