Voronoi Diagrams for Oriented Spheres Franz Aurenhammer Joint


![Power Diagram Theorem [AI, 1988] Separators are hyperplanes iff the diagram is the power Power Diagram Theorem [AI, 1988] Separators are hyperplanes iff the diagram is the power](https://slidetodoc.com/presentation_image_h/06f4eef10e74ef650cb0c0cb2261b7da/image-3.jpg)






- Slides: 14

Voronoi Diagrams for Oriented Spheres Franz Aurenhammer Joint work with M. Peternell H. Pottmann J. Wallner Dagstuhl Seminar Computational Geometry

Voronoi Diagram The classical case …. Size small, easy computation Separators are lines (hyperplanes) Dagstuhl Seminar Computational Geometry 1
![Power Diagram Theorem AI 1988 Separators are hyperplanes iff the diagram is the power Power Diagram Theorem [AI, 1988] Separators are hyperplanes iff the diagram is the power](https://slidetodoc.com/presentation_image_h/06f4eef10e74ef650cb0c0cb2261b7da/image-3.jpg)
Power Diagram Theorem [AI, 1988] Separators are hyperplanes iff the diagram is the power diagram for some set of spheres. Dagstuhl Seminar Computational Geometry 2

Quadratic-form Distance Q(p, q) = (q-p)T · M · (q-p), point sites p, q M nonsingular, k x k T T W. l. o. g. M symmetric: Q(p, q) = ½ (q-p) · (M+M ) · (q-p) Separators are hyperplanes Power diagrams are induced Dagstuhl Seminar Computational Geometry 3

Examples M =I closest-point Voronoi diagram (Eucl. squared) M = -I farthest-point diagram M= ( ) 0 1 1 0 Q(p, q) is twice the area of rectangle T with diagonal pq [CDL] M = diag (1, …, 1, -1) quasi-Euclidean distance Dagstuhl Seminar Computational Geometry 4

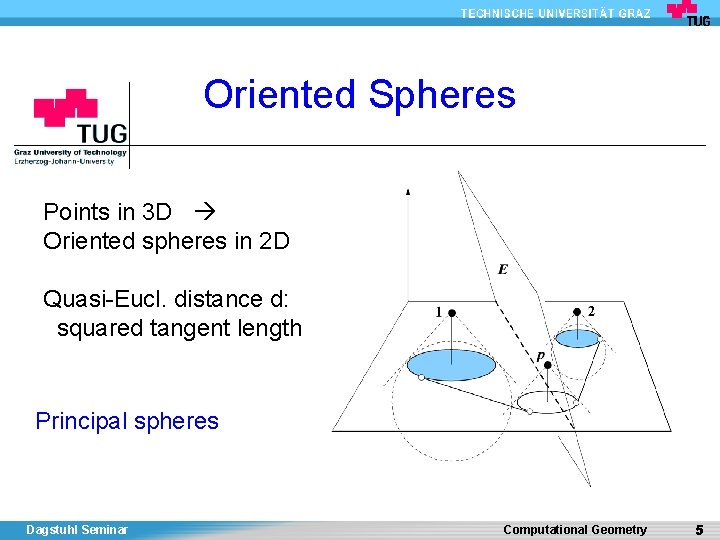
Oriented Spheres Points in 3 D Oriented spheres in 2 D Quasi-Eucl. distance d: squared tangent length Principal spheres Dagstuhl Seminar Computational Geometry 5

Motivation Special relativity: Events = points in quasi-Euclidean space (pseudo-metric governed by M) Isometric mappings = Lorentz transformations Value of d(p, q) is a Lorentz invariant < 0 time-like (√|d| = life time) > 0 space-like (√d = Euclidean distance) = 0 light-like Dagstuhl Seminar Computational Geometry 6

Physical Meaning of d Light cone (d=0) separates time domain (d>0) from space domain (d<0) Dagstuhl Seminar Computational Geometry 7

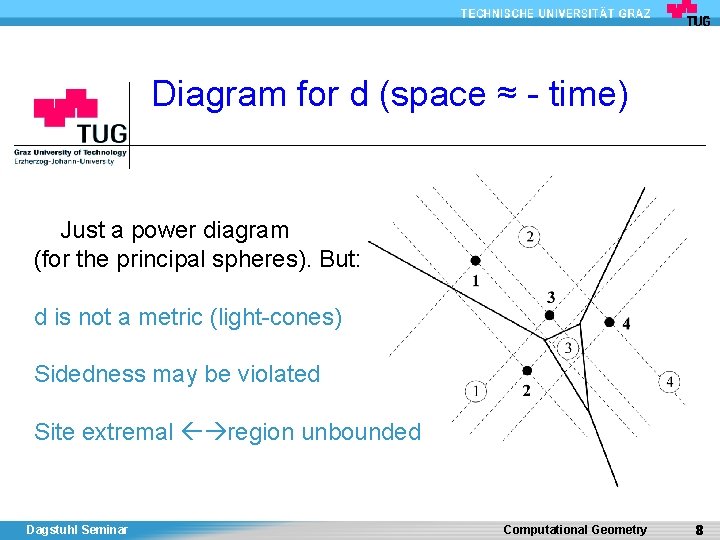
Diagram for d (space ≈ - time) Just a power diagram (for the principal spheres). But: d is not a metric (light-cones) Sidedness may be violated Site extremal region unbounded Dagstuhl Seminar Computational Geometry 8

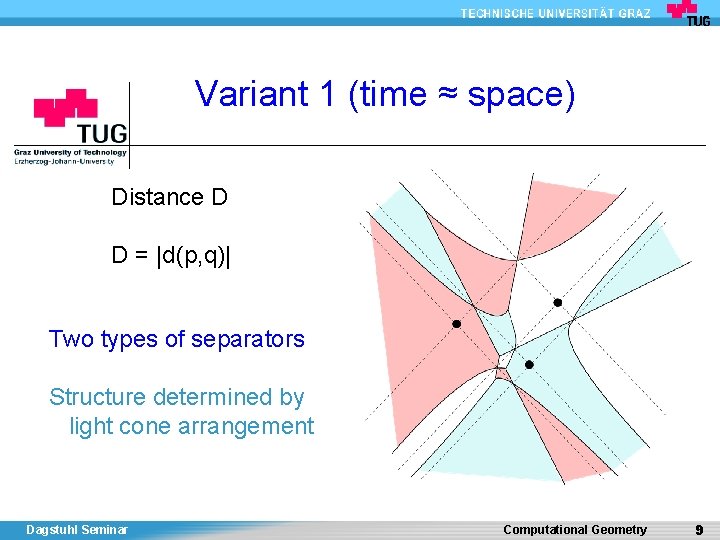
Variant 1 (time ≈ space) Distance D D = |d(p, q)| Two types of separators Structure determined by light cone arrangement Dagstuhl Seminar Computational Geometry 9

Variant 2 (space driven) Distance Δ ∞ = d(p, q) if ≥ 0 {∞ otherwise Refinement of light cone arrangement Not face-to-face Dagstuhl Seminar Computational Geometry 10

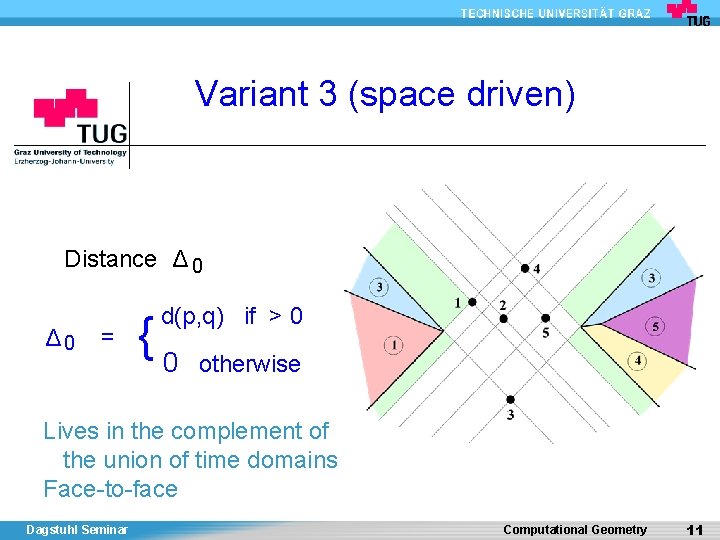
Variant 3 (space driven) Distance Δ 0 = d(p, q) if > 0 {0 otherwise Lives in the complement of the union of time domains Face-to-face Dagstuhl Seminar Computational Geometry 11

What else Associated Delaunay triangulations? Quasi-Euclidean circum-circle…. Dagstuhl Seminar Computational Geometry 12

Thank you Dagstuhl Seminar Computational Geometry 13
 Franz aurenhammer
Franz aurenhammer Voronoi diagram
Voronoi diagram Diagram voronoi
Diagram voronoi Toxic waste dump problem voronoi
Toxic waste dump problem voronoi Matematika mindenkinek
Matematika mindenkinek Voronoi diagram tutorial
Voronoi diagram tutorial The interaction diagrams, use case diagrams are called as
The interaction diagrams, use case diagrams are called as Activity diagrams are static diagrams
Activity diagrams are static diagrams Sales promotion vehicles
Sales promotion vehicles Row oriented database
Row oriented database Memorandum joint venture account format
Memorandum joint venture account format Quality grade of lamb
Quality grade of lamb Ellipsoid joint examples
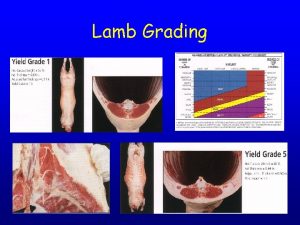
Ellipsoid joint examples Lamb grading chart
Lamb grading chart Costotransverse joint
Costotransverse joint