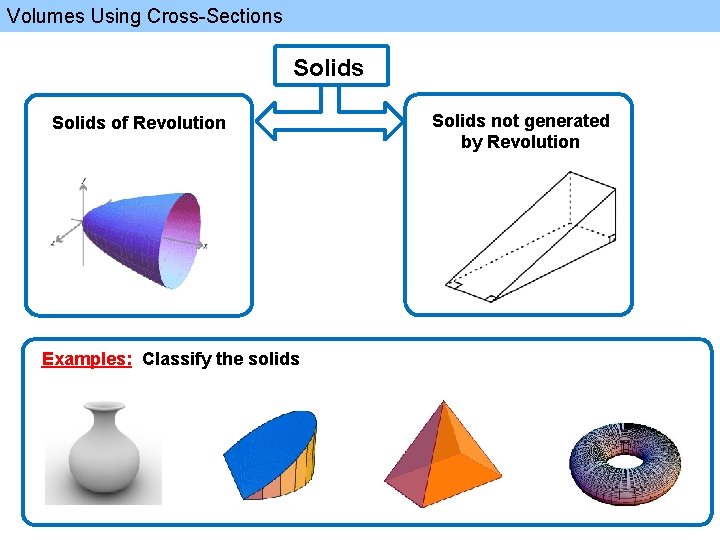
Volumes Using CrossSections Solids of Revolution Examples Classify

Volumes Using Cross-Sections Solids of Revolution Examples: Classify the solids Solids not generated by Revolution

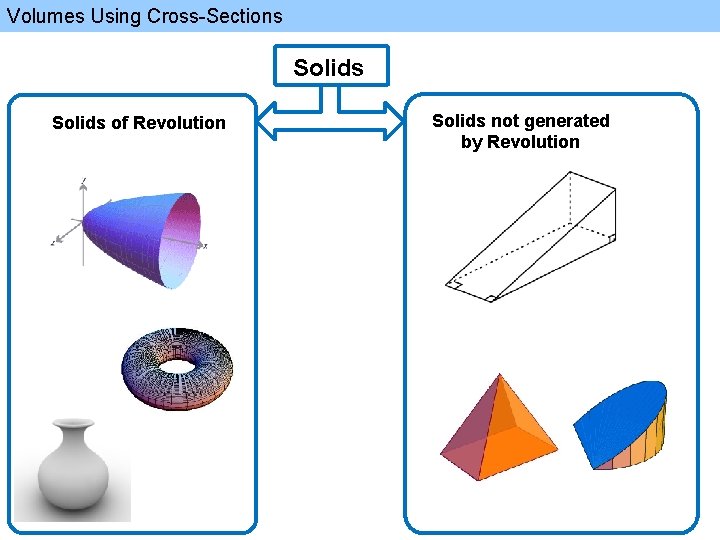
Volumes Using Cross-Sections Solids of Revolution Solids not generated by Revolution

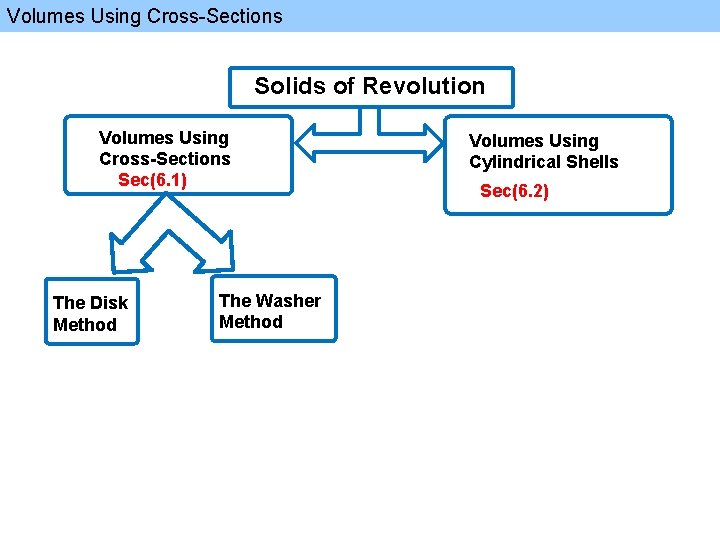
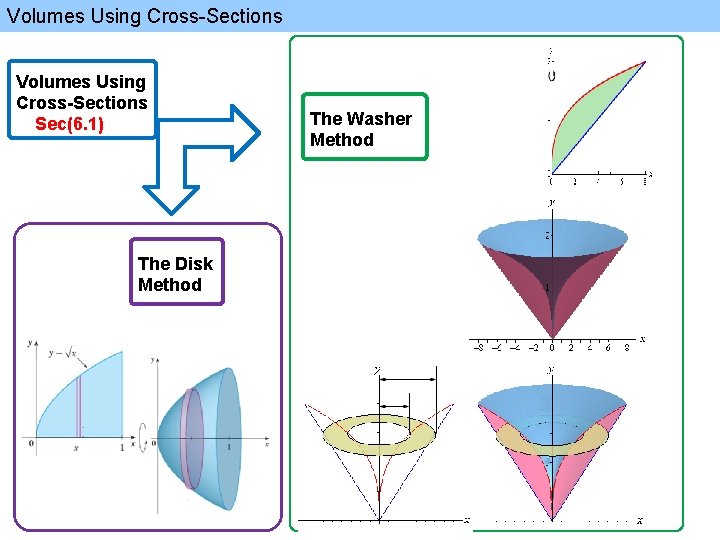
Volumes Using Cross-Sections Solids of Revolution Volumes Using Cross-Sections Sec(6. 1) The Disk Method The Washer Method Volumes Using Cylindrical Shells Sec(6. 2)

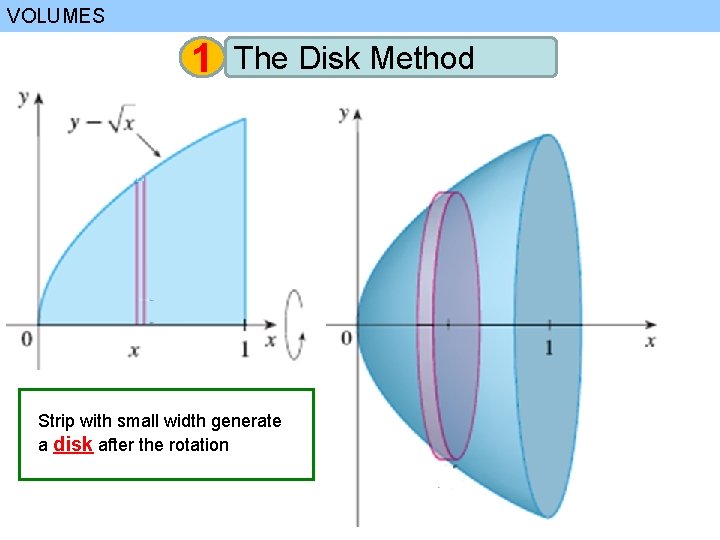
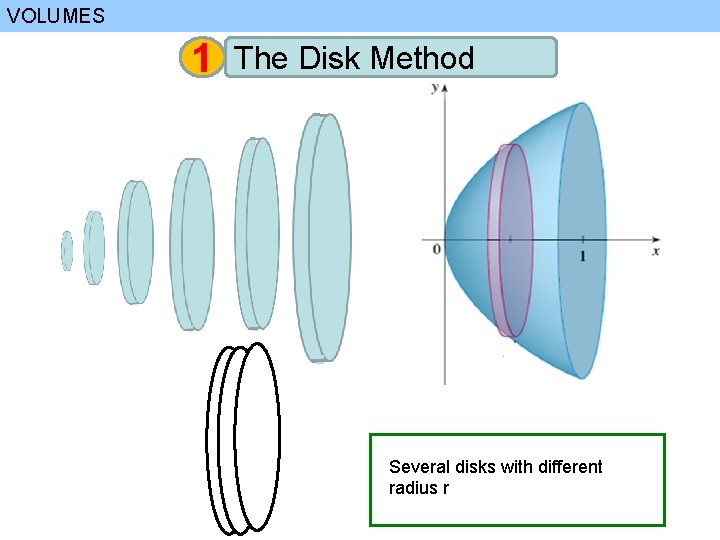
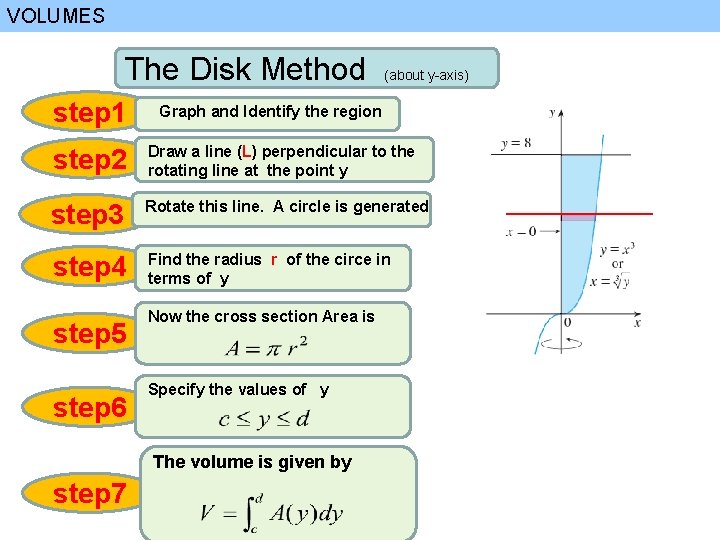
VOLUMES 1 The Disk Method Strip with small width generate a disk after the rotation

VOLUMES 1 The Disk Method Several disks with different radius r

VOLUMES

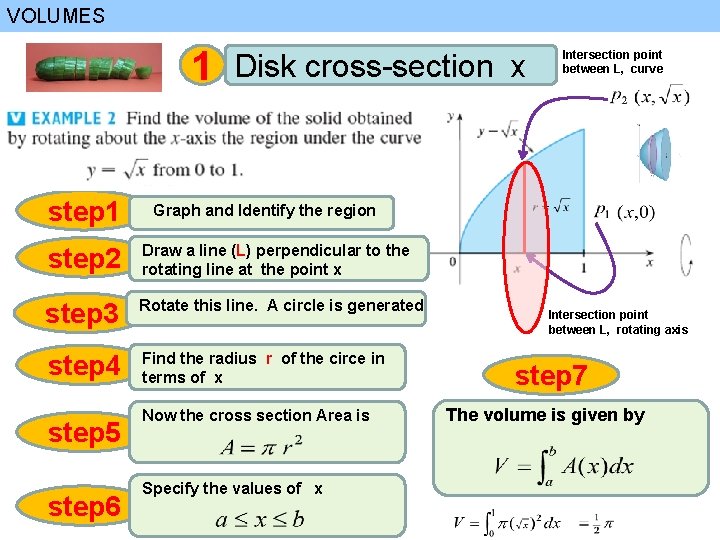
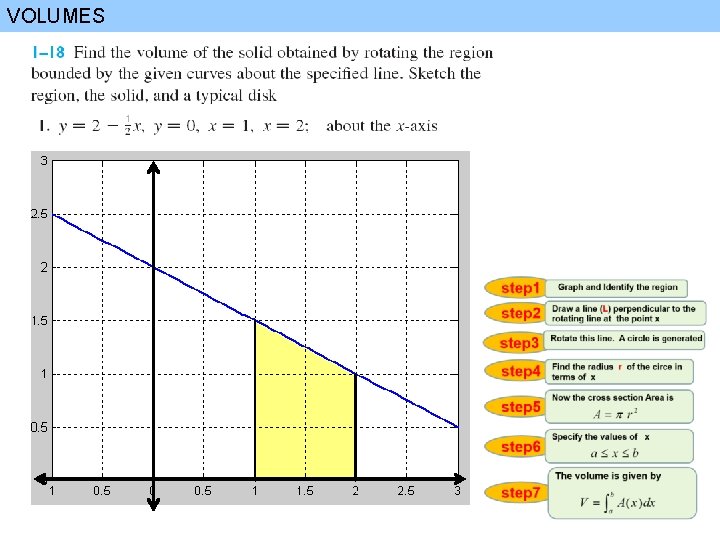
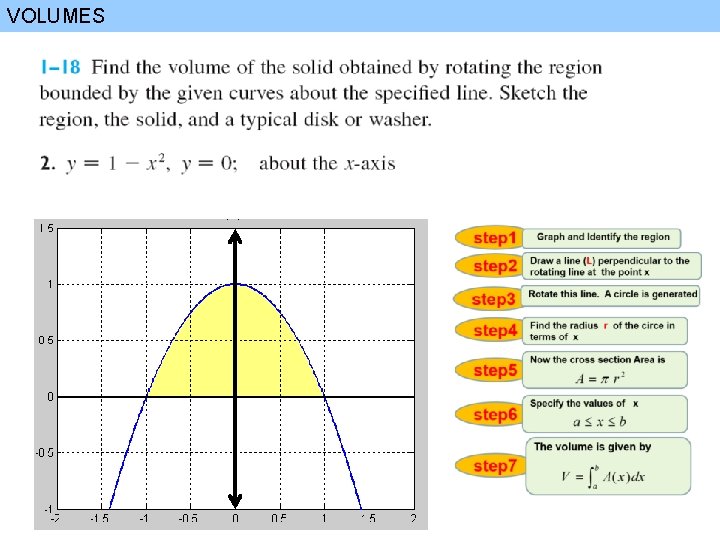
VOLUMES 1 step 1 Disk cross-section x Graph and Identify the region step 2 Draw a line (L) perpendicular to the rotating line at the point x step 3 Rotate this line. A circle is generated step 4 Find the radius r of the circe in terms of x step 5 step 6 Intersection point between L, curve Now the cross section Area is Specify the values of x Intersection point between L, rotating axis step 7 The volume is given by

VOLUMES

VOLUMES

Volumes Using Cross-Sections Sec(6. 1) The Disk Method The Washer Method

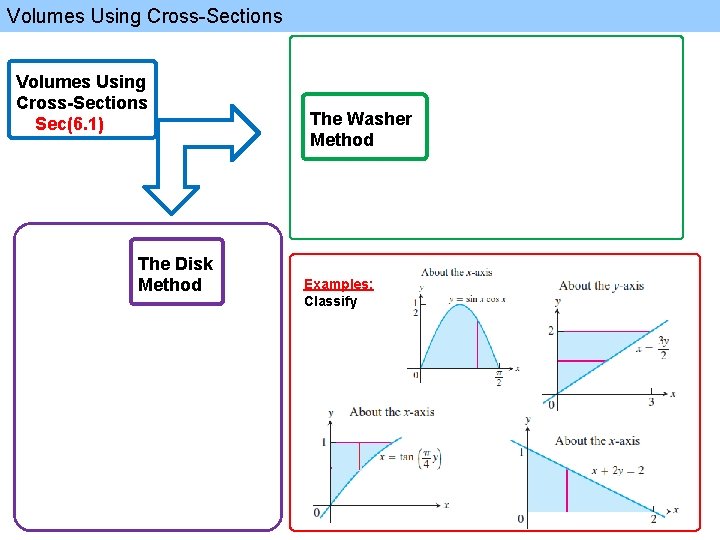
Volumes Using Cross-Sections Sec(6. 1) The Disk Method The Washer Method Examples: Classify

Volumes Using Cross-Sections Sec(6. 1) The Disk Method The Washer Method Examples: Classify

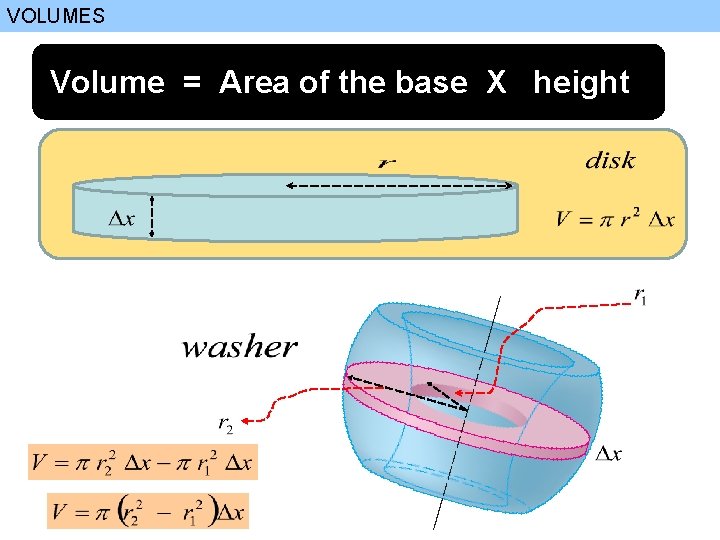
VOLUMES Volume = Area of the base X height

VOLUMES

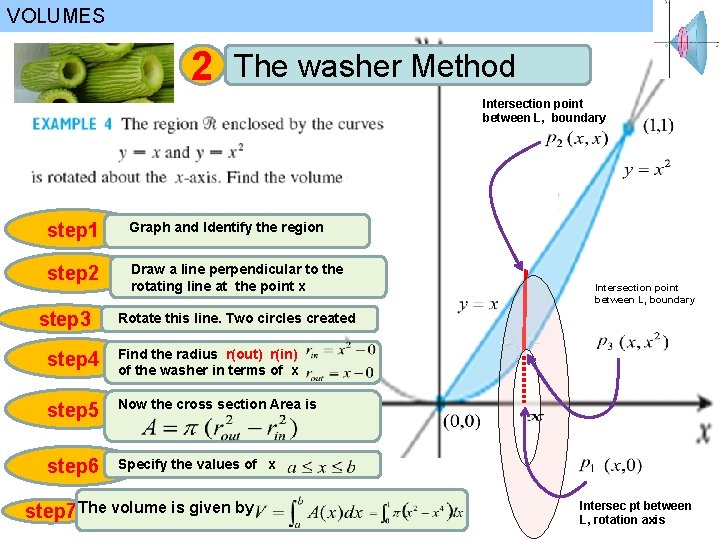
VOLUMES 2 The washer Method If the cross-section is a washer , we find the inner radius and outer radius

VOLUMES 2 The washer Method Intersection point between L, boundary step 1 Graph and Identify the region step 2 Draw a line perpendicular to the rotating line at the point x step 3 Intersection point between L, boundary Rotate this line. Two circles created step 4 Find the radius r(out) r(in) of the washer in terms of x step 5 Now the cross section Area is step 6 Specify the values of x step 7 The volume is given by Intersec pt between L, rotation axis

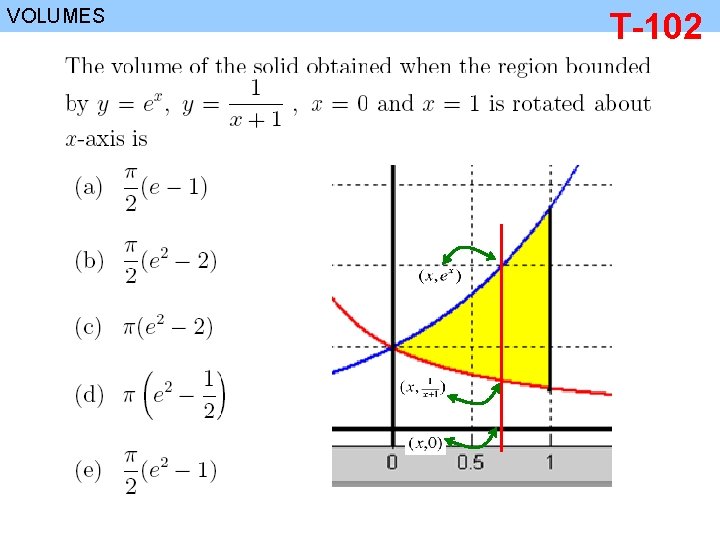
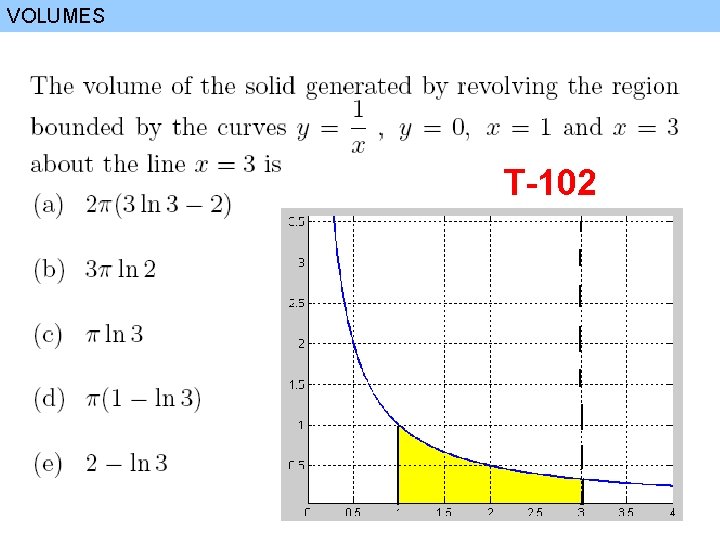
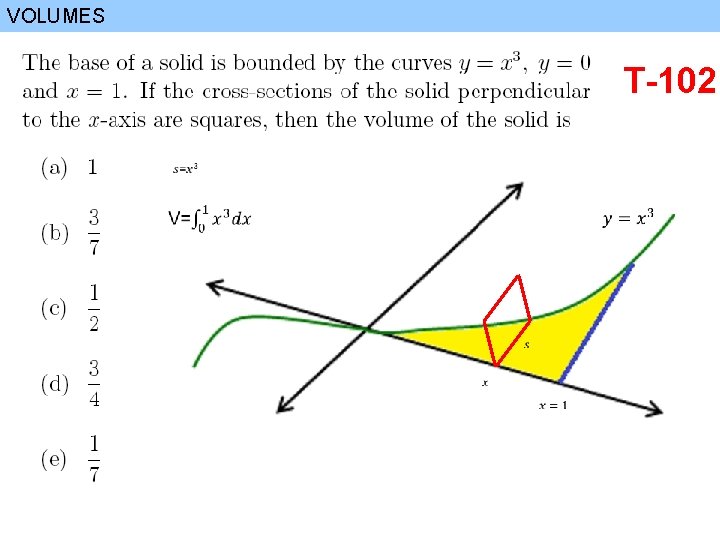
VOLUMES T-102

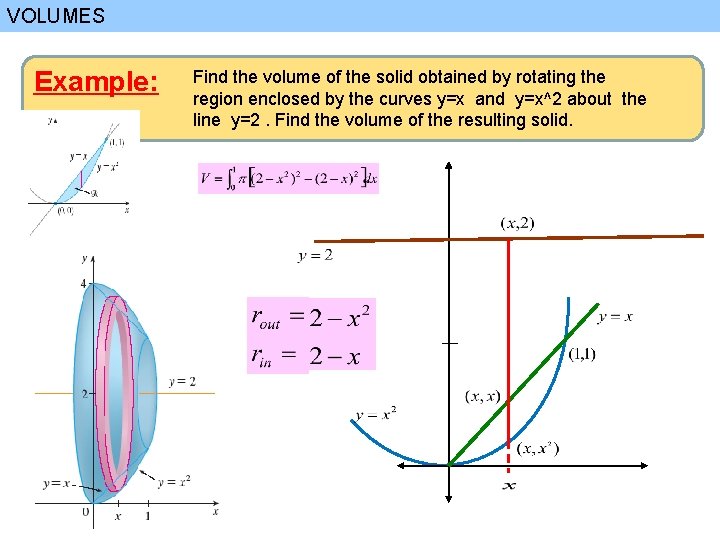
VOLUMES Example: Find the volume of the solid obtained by rotating the region enclosed by the curves y=x and y=x^2 about the line y=2. Find the volume of the resulting solid.

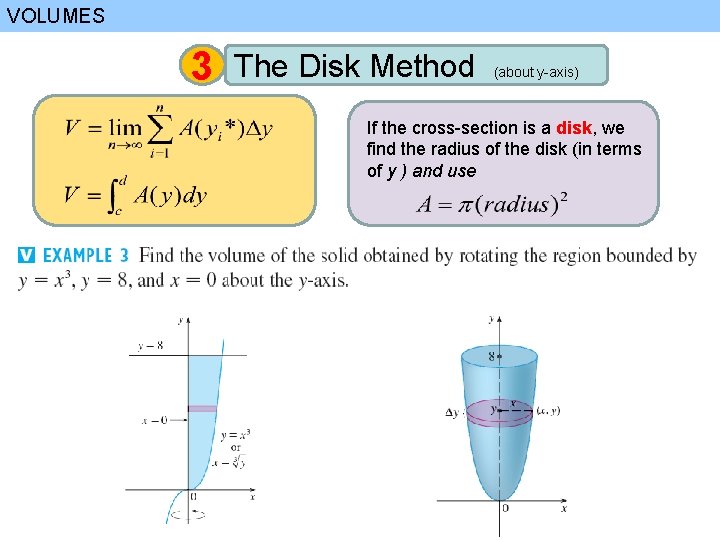
VOLUMES 3 The Disk Method (about y-axis) If the cross-section is a disk, we find the radius of the disk (in terms of y ) and use

VOLUMES The Disk Method step 1 (about y-axis) Graph and Identify the region step 2 Draw a line (L) perpendicular to the rotating line at the point y step 3 Rotate this line. A circle is generated step 4 Find the radius r of the circe in terms of y step 5 step 6 Now the cross section Area is Specify the values of y The volume is given by step 7

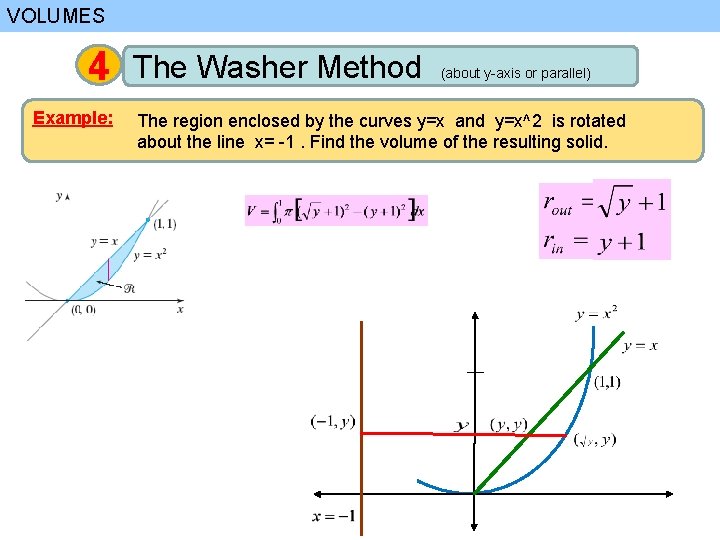
VOLUMES 4 Example: The Washer Method (about y-axis or parallel) The region enclosed by the curves y=x and y=x^2 is rotated about the line x= -1. Find the volume of the resulting solid.

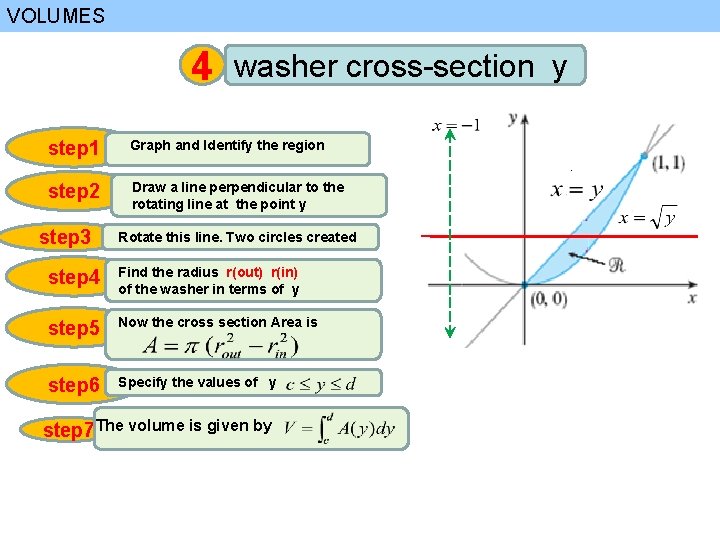
VOLUMES 4 washer cross-section y step 1 Graph and Identify the region step 2 Draw a line perpendicular to the rotating line at the point y step 3 Rotate this line. Two circles created step 4 Find the radius r(out) r(in) of the washer in terms of y step 5 Now the cross section Area is step 6 Specify the values of y step 7 The volume is given by

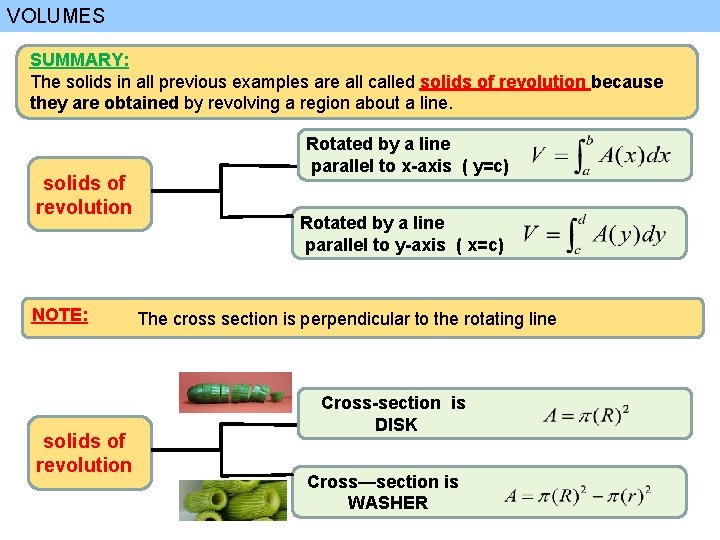
VOLUMES SUMMARY: The solids in all previous examples are all called solids of revolution because they are obtained by revolving a region about a line. solids of revolution NOTE: solids of revolution Rotated by a line parallel to x-axis ( y=c) Rotated by a line parallel to y-axis ( x=c) The cross section is perpendicular to the rotating line Cross-section is DISK Cross—section is WASHER

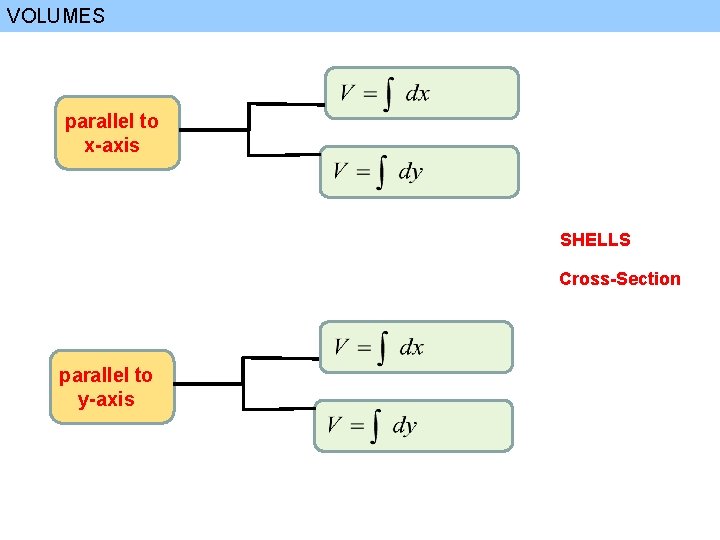
VOLUMES BY CYLINDRICAL SHELLS rotating line Parallel to x-axis CYLINDRICAL SHELLS (6. 2) Remarks rotating line Parallel to y-axis rotating line Parallel to x-axis Remarks Using Cross-Section(6. 1) rotating line Parallel to y-axis Cross-section is DISK Cross—section is WASHER SHELL Method

VOLUMES parallel to x-axis SHELLS Cross-Section parallel to y-axis

VOLUMES BY CYLINDRICAL SHELLS T-131 Remark: before you start solving the problem, read the choices to figure out which method you use

T-111

VOLUMES T-102

Volumes Using Cross-Sections Solids of Revolution Solids not generated by Revolution

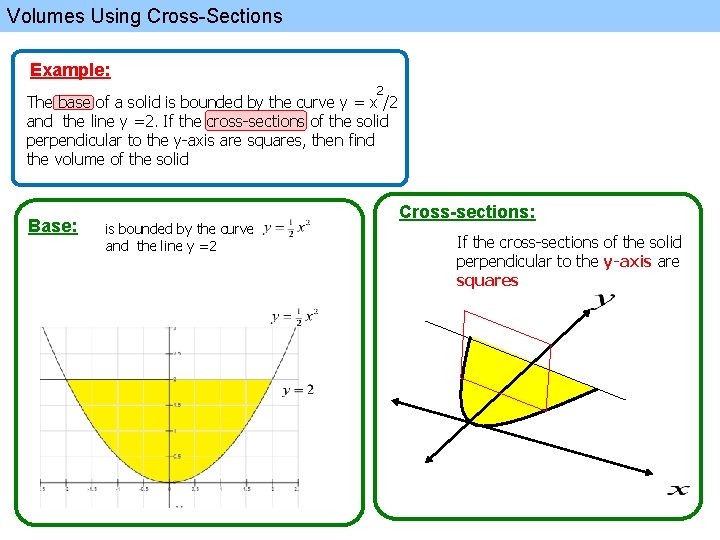
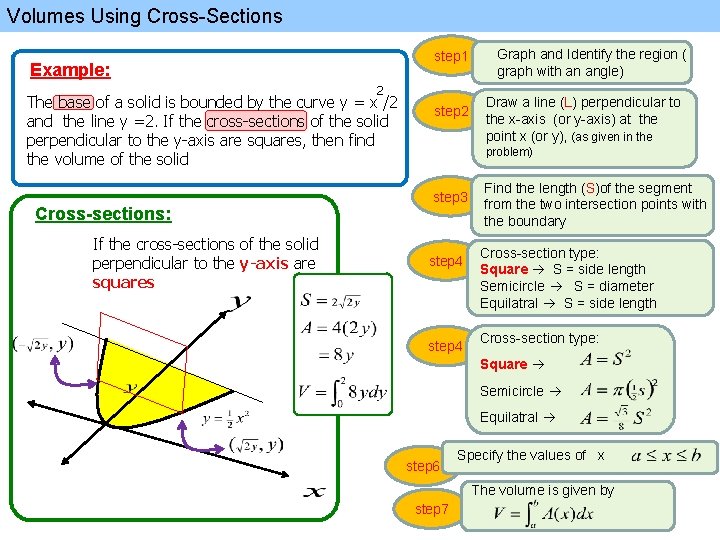
Volumes Using Cross-Sections Example: 2 The base of a solid is bounded by the curve y = x /2 and the line y =2. If the cross-sections of the solid perpendicular to the y-axis are squares, then find the volume of the solid Base: is bounded by the curve and the line y =2 Cross-sections: If the cross-sections of the solid perpendicular to the y-axis are squares

VOLUMES Jonathan Mitchell

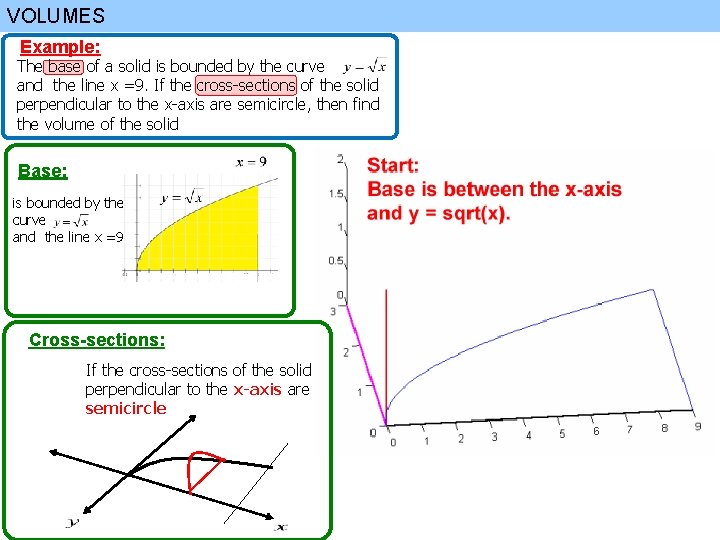
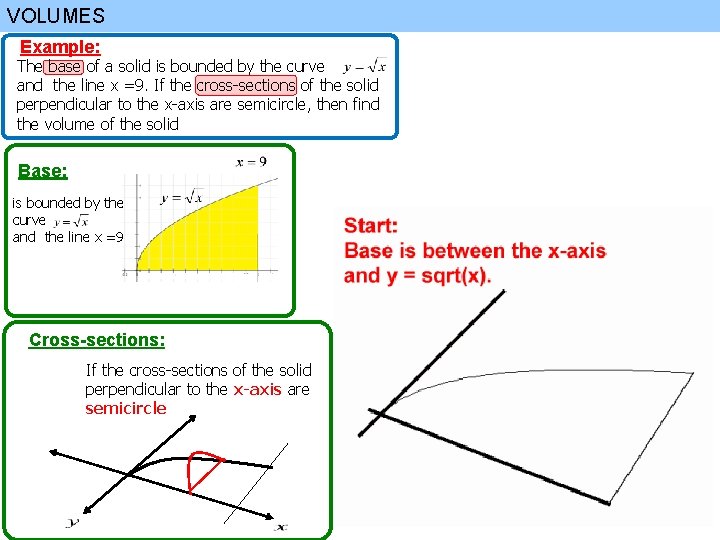
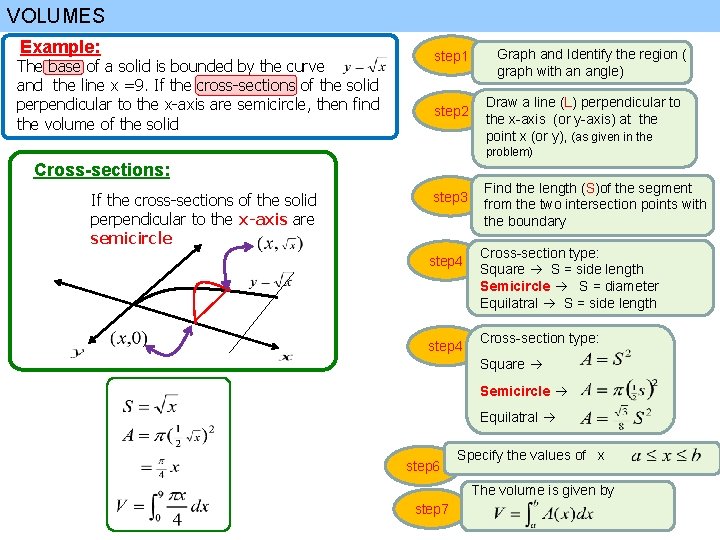
VOLUMES Example: The base of a solid is bounded by the curve and the line x =9. If the cross-sections of the solid perpendicular to the x-axis are semicircle, then find the volume of the solid Base: is bounded by the curve and the line x =9 Cross-sections: If the cross-sections of the solid perpendicular to the x-axis are semicircle

VOLUMES Example: The base of a solid is bounded by the curve and the line x =9. If the cross-sections of the solid perpendicular to the x-axis are semicircle, then find the volume of the solid Base: is bounded by the curve and the line x =9 Cross-sections: If the cross-sections of the solid perpendicular to the x-axis are semicircle

VOLUMES Example: The base of a solid is bounded by the curve and the line x =9. If the cross-sections of the solid perpendicular to the x-axis are semicircle, then find the volume of the solid Base: is bounded by the curve and the line x =9 Cross-sections: If the cross-sections of the solid perpendicular to the x-axis are semicircle

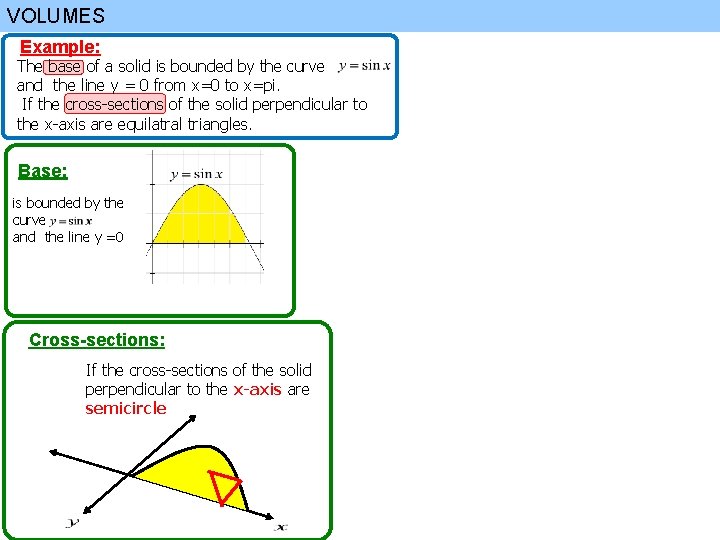
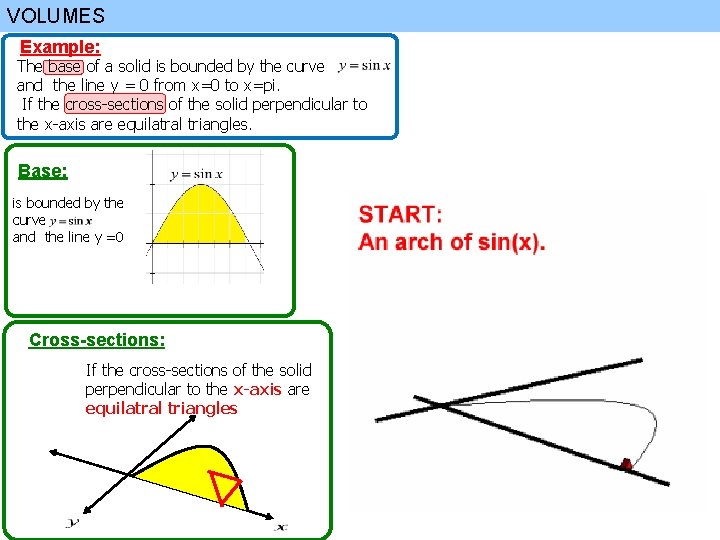
VOLUMES Example: The base of a solid is bounded by the curve and the line y = 0 from x=0 to x=pi. If the cross-sections of the solid perpendicular to the x-axis are equilatral triangles. Base: is bounded by the curve and the line y =0 Cross-sections: If the cross-sections of the solid perpendicular to the x-axis are semicircle

VOLUMES Example: The base of a solid is bounded by the curve and the line y = 0 from x=0 to x=pi. If the cross-sections of the solid perpendicular to the x-axis are equilatral triangles. Base: is bounded by the curve and the line y =0 Cross-sections: If the cross-sections of the solid perpendicular to the x-axis are equilatral triangles

Volumes Using Cross-Sections step 1 Example: 2 The base of a solid is bounded by the curve y = x /2 and the line y =2. If the cross-sections of the solid perpendicular to the y-axis are squares, then find the volume of the solid Cross-sections: If the cross-sections of the solid perpendicular to the y-axis are squares step 2 Graph and Identify the region ( graph with an angle) Draw a line (L) perpendicular to the x-axis (or y-axis) at the point x (or y), (as given in the problem) step 3 step 4 Find the length (S)of the segment from the two intersection points with the boundary Cross-section type: Square S = side length Semicircle S = diameter Equilatral S = side length Cross-section type: Square Semicircle Equilatral step 6 Specify the values of x The volume is given by step 7

VOLUMES Example: The base of a solid is bounded by the curve and the line x =9. If the cross-sections of the solid perpendicular to the x-axis are semicircle, then find the volume of the solid step 1 step 2 Graph and Identify the region ( graph with an angle) Draw a line (L) perpendicular to the x-axis (or y-axis) at the point x (or y), (as given in the problem) Cross-sections: If the cross-sections of the solid perpendicular to the x-axis are semicircle step 3 step 4 Find the length (S)of the segment from the two intersection points with the boundary Cross-section type: Square S = side length Semicircle S = diameter Equilatral S = side length Cross-section type: Square Semicircle Equilatral step 6 Specify the values of x The volume is given by step 7

VOLUMES T-102

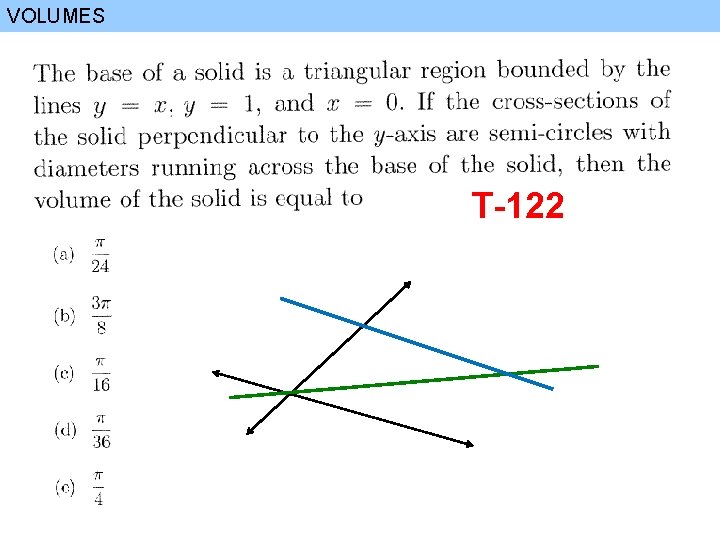
VOLUMES T-122

VOLUMES T-092

VOLUMES

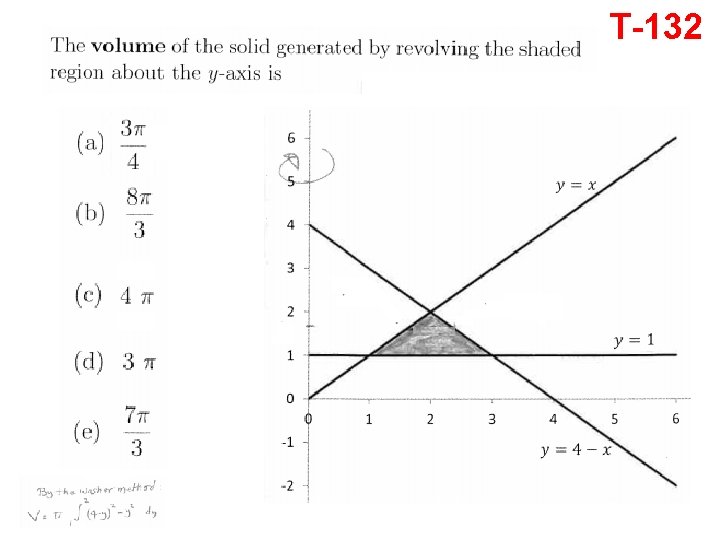
T-132

T-132