Volumes The Disk Method Textbook 7 2 Overview

Volumes – The Disk Method Textbook 7. 2 Overview on Page 456

Revolving a Function • We have a function f(x) on the interval [a, b] a • What happens when we b revolve that segment of curve about the x axis? • What kind of functions generated these solids of revolution?

Disks f(x) • We can use integrals to determine the volume of these solids • Here we have a disk • which is a slice of the solid § What is the radius? § What is the thickness? § What then, is its volume? dx

Disks • To find the volume of the whole solid we sum the volumes of the disks • Shown as a definite integral f(x) a b

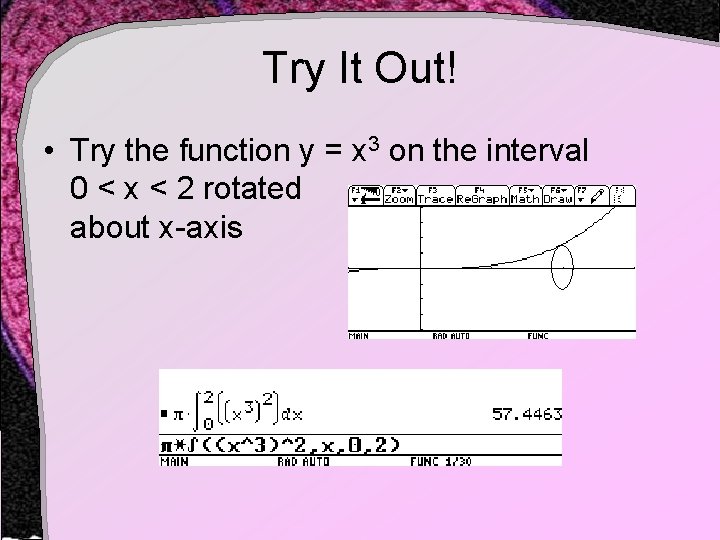
Try It Out! • Try the function y = x 3 on the interval 0 < x < 2 rotated about x-axis

Revolve About Line Not a Coordinate Axis • Consider the function y = 2 x 2 and the boundary lines y = 0, x = 2 • Revolve this region about the line x = 2 • We need an expression for the radius in terms of y

Washers • Consider the area between two functions rotated about the axis f(x) g(x) a • Now we have a hollow solid • We will sum the volumes of washers • As an integral b

Application • Given two functions y = x 2, and y = x 3 § Revolve region between about x-axis What will be the limits of integration?

Revolving About y-Axis • Also possible to revolve a function about the y-axis § Make a disk or a washer to be horizontal • Consider revolving a parabola about the y-axis § How to represent the radius? § What is the thickness of the disk?

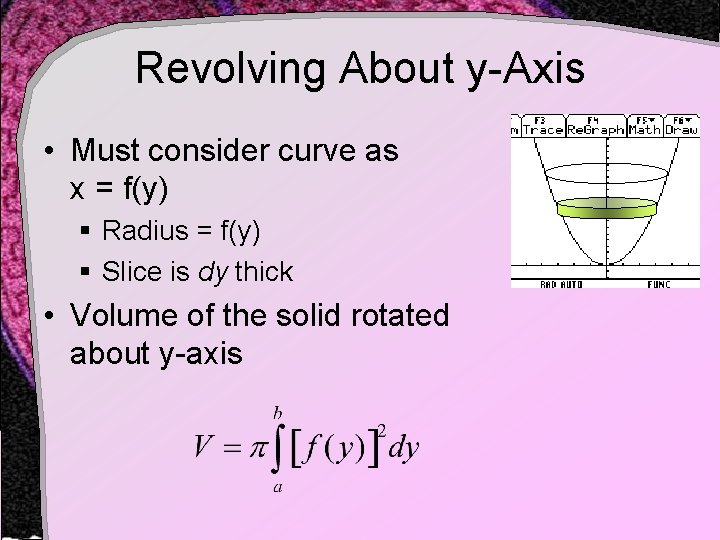
Revolving About y-Axis • Must consider curve as x = f(y) § Radius = f(y) § Slice is dy thick • Volume of the solid rotated about y-axis

Flat Washer • Determine the volume of the solid generated by the region between y = x 2 and y = 4 x, revolved about the y-axis § Radius of inner circle? • f(y) = y/4 § Radius of outer circle? • § Limits? • 0 < y < 16