Volumes The Disk Method Lesson 7 2 Revolving

Volumes – The Disk Method Lesson 7. 2

Revolving a Function • Consider a function f(x) on the interval [a, b] a • Now consider revolving b that segment of curve about the x axis • What kind of functions generated these solids of revolution?

Revolving a Function • What kind of function here?

Disks f(x) • We seek ways of using integrals to determine the volume of these solids • Consider a disk which is a slice of the solid § What is the radius § What is the thickness § What then, is its volume? dx

Disks • To find the volume of the whole solid we sum the volumes of the disks • Shown as a definite integral f(x) a b

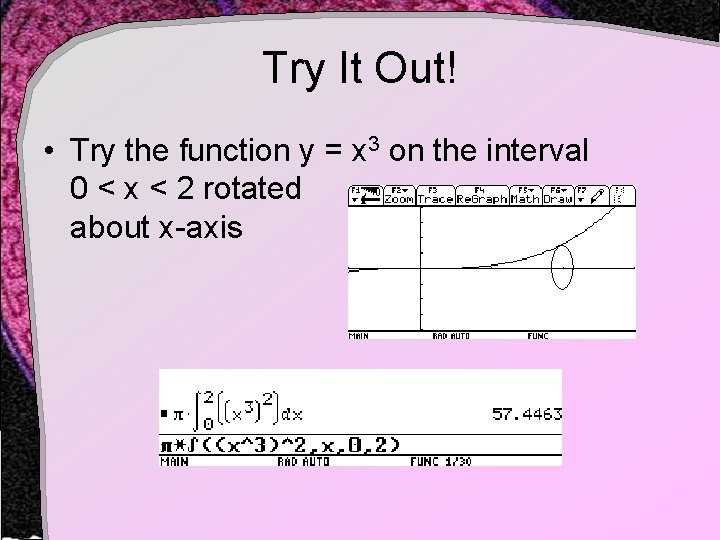
Try It Out! • Try the function y = x 3 on the interval 0 < x < 2 rotated about x-axis

Revolve About Line Not a Coordinate Axis • Consider the function y = 2 x 2 and the boundary lines y = 0, x = 2 • Revolve this region about the line x = 2 • We need an expression for the radius in terms of y

Washers • Consider the area between two functions rotated about the axis f(x) g(x) a • Now we have a hollow solid • We will sum the volumes of washers • As an integral b

Application • Given two functions y = x 2, and y = x 3 § Revolve region between about x-axis What will be the limits of integration?

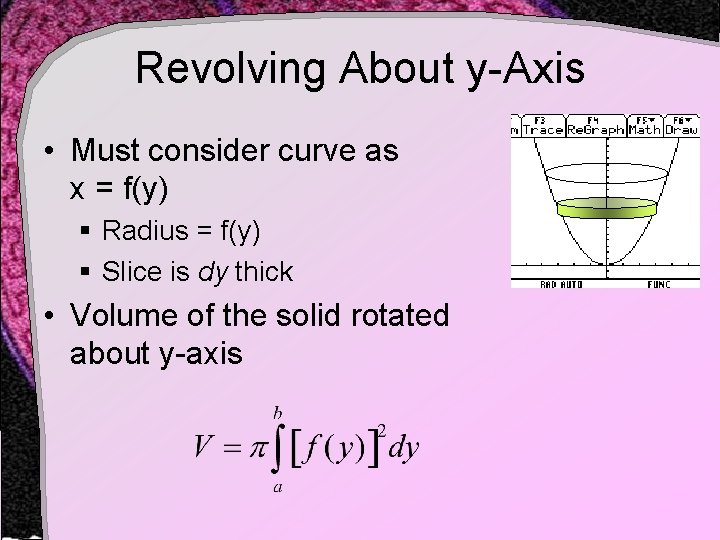
Revolving About y-Axis • Also possible to revolve a function about the y-axis § Make a disk or a washer to be horizontal • Consider revolving a parabola about the y-axis § How to represent the radius? § What is the thickness of the disk?

Revolving About y-Axis • Must consider curve as x = f(y) § Radius = f(y) § Slice is dy thick • Volume of the solid rotated about y-axis

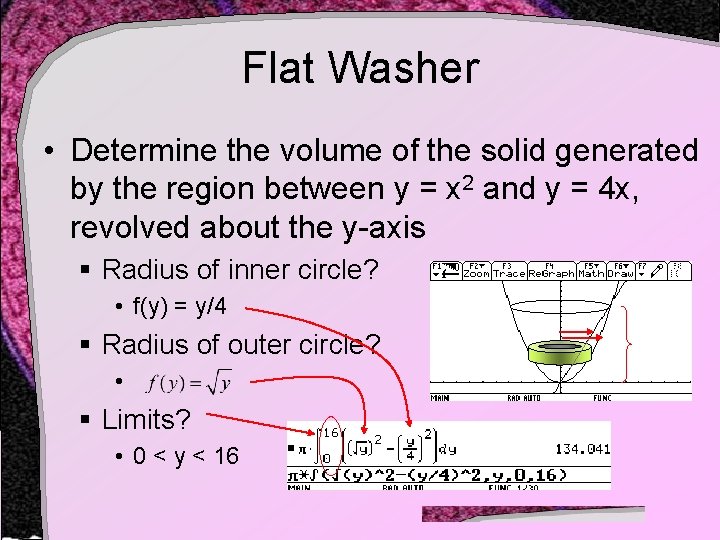
Flat Washer • Determine the volume of the solid generated by the region between y = x 2 and y = 4 x, revolved about the y-axis § Radius of inner circle? • f(y) = y/4 § Radius of outer circle? • § Limits? • 0 < y < 16

Assignment A • Lesson 7. 2 A • Page 463 • Exercises 1 – 29 odd • Spreadsheet Assignment Due in 1 Week

Cross Sections • Consider a square at x = c with side equal to side s = f(c) • Now let this be a thin slab with thickness Δx • What is the volume of the slab? • Now sum the volumes of all such slabs

Cross Sections • This suggests a limit and an integral

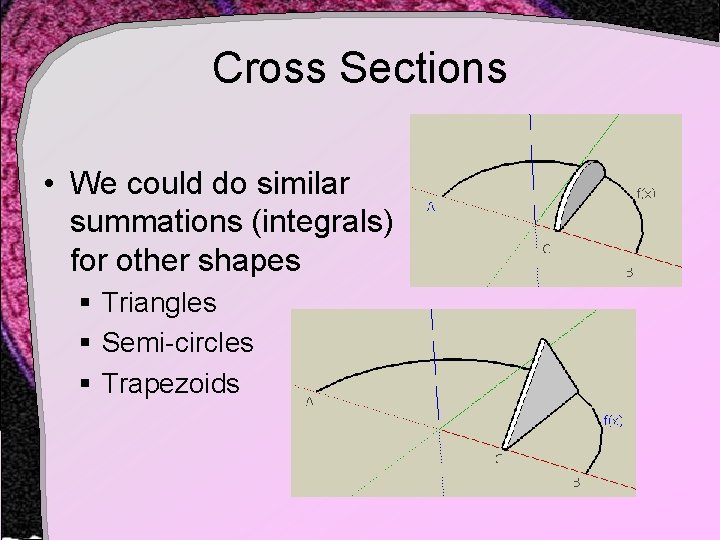
Cross Sections • We could do similar summations (integrals) for other shapes § Triangles § Semi-circles § Trapezoids

Try It Out • Consider the region bounded § above by y = cos x § below by y = sin x § on the left by the y-axis • Now let there be slices of equilateral triangles erected on each cross section perpendicular to the x-axis • Find the volume

Assignment • Lesson 7. 2 B • Page 464 • Exercises 31 - 39 odd, 49, 53, 57