VOLUME What is Volume Volume is the measure








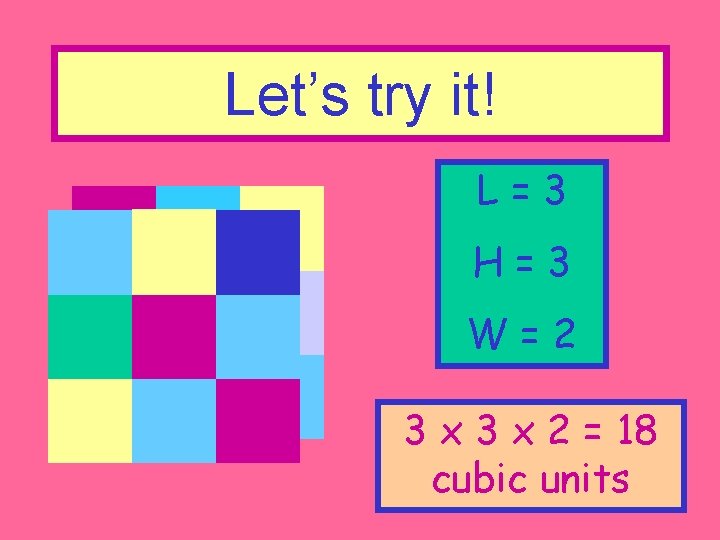








- Slides: 18

VOLUME

What is Volume? • Volume is the measure of the capacity of a container. • It is the measure of how much a container of a particular shape will hold - liquids, dry substances, etc.

VOLUME is the amount of liquid or solid that will FILL a 3 -Dimensional object! *Always measured in units cubed (u 3)

QUICK DEFINITION • 3 -Dimensional objects are NOT FLAT. • They have 3 measurements: –Length –Width –Height

Cubic Units ¤Volume is measured in cubic units. ¤Use cubes to fill a rectangular prism such as a box.

RECTANGULAR PRISM • The volume of a 3 -D object called a RECTANGULAR PRISM, which is a solid figure that has six faces that are all rectangles. Opposite faces are congruent and parallel.

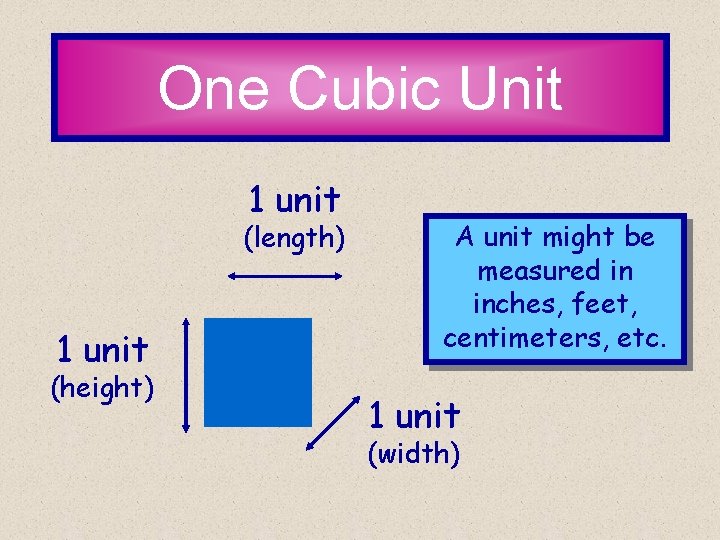
One Cubic Unit 1 unit (length) 1 unit (height) A unit might be measured in inches, feet, centimeters, etc. 1 unit (width)

How many cubic units is this rectangle? What did you find? Yes, it is 8 cubic units!

What’s the formula? The formula for finding the volume of a rectangle is …. L x W x H = Volume This means we take the length times the width, then multiply that by the height.
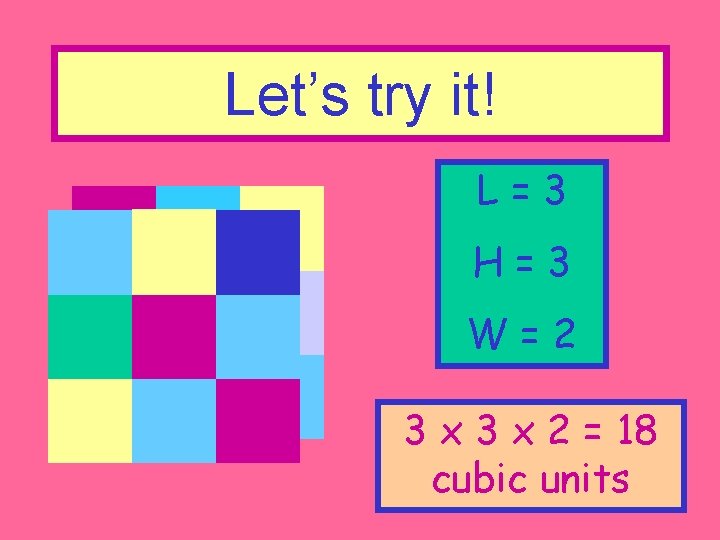
Let’s try it! L=3 H=3 W=2 3 x 2 = 18 cubic units

Find the volume of this one! What did you find? 4 x 2 x 3 = 24 cubic units

FIND THE VOLUME OF THIS RECTANGULAR PRISM: 3 mm 2 mm 12 mm

Let’s practice some problems and solving them. A cereal box has a length of 8 inches, a width of 1. 75 inches, and a height of 12. 125 inches. How much cereal will the box hold?

Alexis’s bathroom has a tub in the shape of a rectangular prism with a length of 1. 5 meters, a width of 0. 5 meter, and a height of 0. 4 meter. How many cubic meters of water can it hold?

Now let’s try a more challenging problem.

Be Careful! You must convert 3 feet to inches. Subtract and then convert back to feet.

Length x Width x Height Length = 12 feet Width = 2 feet Height = 30 inches or 2 ½ feet A Length x Width x Height 12 x 2 ½ 24 x 2 ½ 60

BINGO Let’s Practice finding Volume
 Uses of wind vane
Uses of wind vane Gibbons jacobean city comedy download
Gibbons jacobean city comedy download Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Bổ thể
Bổ thể Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Phối cảnh
Phối cảnh điện thế nghỉ
điện thế nghỉ Một số thể thơ truyền thống
Một số thể thơ truyền thống Bài hát chúa yêu trần thế alleluia
Bài hát chúa yêu trần thế alleluia Sơ đồ cơ thể người
Sơ đồ cơ thể người Thế nào là số nguyên tố
Thế nào là số nguyên tố đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công của trọng lực
Công của trọng lực Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em ưu thế lai là gì
ưu thế lai là gì Thẻ vin
Thẻ vin



































