Volume Surface Area Volume Surface Area Objectives 7

Volume & Surface Area

Volume & Surface Area Objectives: 7. 2. 02 Solve problems involving volume and surface area of cylinders, prisms, and composite shapes. Essential Question: How can I use what I know about area to calculate volume and surface area of cubes, prisms, and cylinders?

Volume & Surface Area Cube: a 3 D shape with six square or rectangular sides, a block. Rectangular Prism: a polyhedron that has two parallel and congruent bases that are rectangles; a 3 D solid with six rectangular faces. Triangular Prism: a polyhedron that has two parallel, congruent bases that are triangles; a prism whose faces are triangles. Cylinder: a 3 D figure that has two parallel congruent bases. Volume: the measure of space occupied by a solid region. Surface Area: the sum of the areas of all the surfaces (faces) of a three dimensional figure.

Volume & Surface Area Triangular Pyramid: a polyhedron with a three-sided polygon for a base and triangles for its sides; a pyramid with a triangular base. Square Pyramid: a polyhedron with a four-sided polygon for a base and triangles for its sides; a pyramid with a square base. Sphere: a perfectly rounded 3 D object such as a ball. Cone: a 3 D figure with one circular base.

Volume & Surface Area What is a 3 D Figure: What do they look like… In previous years you have studied 2 D shapes like squares, rectangles, parallelograms, triangles, circles, and trapezoids. But now it is time to add a third dimension…

Volume & Surface Area What is a 3 D Figure: What do they look like…

Volume & Surface Area Some 3 D Figures: What do they look like… Cube Rectangular Prism Triangular Prism Cylinder

Volume & Surface Area Some Additional 3 D Figures: What do they look like… Triangular Pyramid Square Pyramid Sphere Cone

Volume & Surface Area Cubes: What do they look like…

Volume & Surface Area Prisms: What do they look like…

Volume & Surface Area Cylinders: What do they look like…

Volume & Surface Area 3 D Characteristics: What makes what a what… A 3 D shape with two parallel congruent polygon bases

Volume & Surface Area 3 D Characteristics: What makes what a what… A cylinder falls under its own category because its bases are not considered polygons

Volume & Surface Area 3 D Characteristics: What makes what a what… Others include pyramids and cones because they contain only one base. Their name is derived based on the shape of the base

Volume & Surface Area Important Volume Formulas: Cube V = s 3 Rectangular Prism Triangular Prism Cylinder V = lwh V = bhw V = ½bhw V = πr 2 h

Volume & Surface Area Example 1: Cube Find the volume of the cube whose sides measure 3 inches. Volume = s 3 V = 3 in x 3 in V = 27 in 3

Volume & Surface Area Example 1: Rectangular Prism Find the volume of the rectangular prism whose length is 5 in, width is 9 in, and height is 4 in. Volume = lwh V = 5 in x 9 in x 4 in V = 180 in 3

Volume & Surface Area Example 1: Triangular Prism Find the volume of the triangular prism whose length is 6 cm, width is 4 cm, and height is 3 cm. Volume = ½bhw V = ½(6 cm)(3 cm)(4 cm) V = 36 cm 3

Volume & Surface Area Example 1: Cylinder Find the volume of the cylinder whose height is 3 ft and radius is 4 ft. Volume = πr 2 h V = (3. 14)(4 ft)2(3 ft) V = 150. 72 ft 3

Volume & Surface Area Example 1: Rectangular Prism Find the volume of the rectangular prism. V = lwh V = 4 in x 6 in x 5 in V = 120 in 3

Volume & Surface Area Example 1: Rectangular Prism Find the volume of the rectangular prism. V = lwh V = 5 in x 7 in x 11 in V = 385 in 3

Volume & Surface Area Example 1: Triangular Prism Find the volume of the triangular prism. Volume = ½bhw V = ½(15 cm)(9 cm)(4 cm) V = 270 cm 3

Volume & Surface Area Example 1: Cylinder Find the volume of the cylinder. Volume = πr 2 h V = (3. 14)(3 cm)2(12 cm) V ≈ 339. 3 cm 3

Volume & Surface Area Independent Practice: Volume Find the volume of each 3 d shape. 1. 2. 3. 4.

Volume & Surface Area Independent Practice: Volume Answers. 1. 27 m 3 2. 1260 cm 3 3. 27 m 3 4. 336 mm 3

Volume & Surface Area Find the volume of the block. A wooden block has a single hole drilled entirely through it. What is the volume of the block? Round to the nearest hundredth. The block is a rectangular prism with a cylindrical hole. To find the volume of the block, subtract the volume of the cylinder from the volume of the prism.

Volume & Surface Area Find the volume of the block. A wooden block has a single hole drilled entirely through it. What is the volume of the block? Round to the nearest hundredth. The volume of the box is about 72 – 9. 42 = 62. 58 cubic centimeters.

Volume & Surface Area Find the volume of the cube. A moving company has boxes of various sizes for packing. The smallest box available has the dimensions shown below. Find the volume of a larger box that is 3 times as large. 12 in. Answer

Volume & Surface Area Find the volume of the cylinder. A jumbo-size can of tomato soup is about 3 times the size of a standardsized can of soup. The standard can has the dimensions shown. Find the surface area and volume of the jumbo-size can. Answer

Volume & Surface Area Formula Summary: Cube V = s 3 Rectangular Prism Triangular Prism Cylinder V = lwh V = bhw V = ½bhw V = πr 2 h

Volume & Surface Area So What’s The Difference: Now that we have studied volume it is time to move on to surface area…another important concept dealing with 3 D shapes: When you think about the words SURFACE AREA What comes to mind?

Volume & Surface Area & Nets: When thinking about surface area we need to be able to break down the 3 D solid by its faces…for instance: If took the above cube and cut along the edges we could open the solid and see that there a total of 6 squares (we call these faces) – the figure on the right is called a net

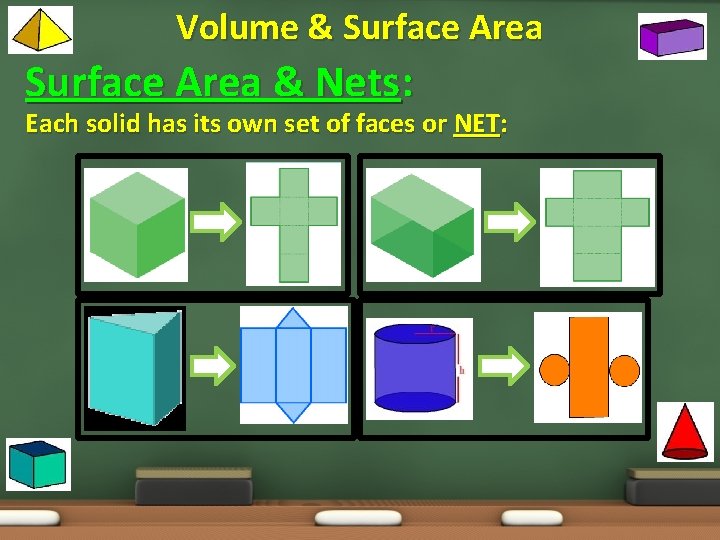
Volume & Surface Area & Nets: Each solid has its own set of faces or NET:

Volume & Surface Area Important Surface Area Formulas: Cube Rectangular Prism SA = 6 s 2 SA = 2 lw + 2 lh + 2 hw

Volume & Surface Area Important Surface Area Formulas: Triangular Prism SA = 2(½bh) + lw 1 + lw 2 + lw 3 Cylinder SA = 2πr 2 + 2πrh

Volume & Surface Area Example 1: Cube Find the surface area. SA = 6 s 2 SA = 6(4 in)2 SA = 6(16 in 2) SA = 96 in 2

Volume & Surface Area Example 1: Rectangular Prism Find the surface area. SA = 2 lw + 2 lh + 2 wh SA = 2(15)(9) + 2(15)(7) + 2(9)(7) SA = 270 mm 2 + 210 mm 2 + 126 mm 2 SA = 606 mm 2

Volume & Surface Area Example 1: Triangular Prism Find the surface area. SA = 2(½bh) + lw 1 + lw 2 + lw 3 SA = 2(½)(4. 5)(3) + (6 x 3. 75) + (6 x 4. 5) SA = 13. 5 in 2 + 22. 5 in 2 + 27 in 2 SA = 85. 5 in 2

Volume & Surface Area Example 1: Cylinder Find the surface area. SA = 2πr 2 + 2πrh SA = 2(3. 14)(3 mm)2 + 2(3. 14)(3 mm)(8 mm) SA = 56. 52 mm 2 + 150. 72 mm 2 SA = 207. 24 mm 2

Volume & Surface Area Camping. A family wants to reinforce the fabric of its tent with a waterproofing treatment. Find the surface area, including the floor, of the tent below. Remember, a triangular prism consists of two congruent triangular faces and three rectangular faces.

Volume & Surface Area Camping. A family wants to reinforce the fabric of its tent with a waterproofing treatment. Find the surface area, including the floor, of the tent below. BOTTOM LEFT SIDE RIGHT SIDE TWO BASES SA = 29 + 36. 54 + 29 = 131. 08

Volume & Surface Area HOMEWORK