Volume Our first example is the volume of

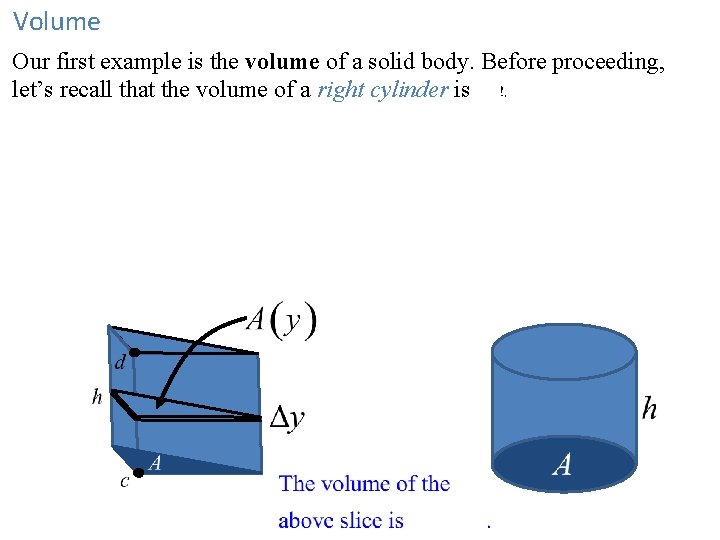
Volume Our first example is the volume of a solid body. Before proceeding, let’s recall that the volume of a right cylinder is Ah. Here we use the “right cylinder” in the general sense; the base does not have to be circular, but the sides are perpendicular to the base. Suppose that the solid body extends from height y = c to y = d along the y-axis. Let A(y) be the area of the horizontal cross section at height y.

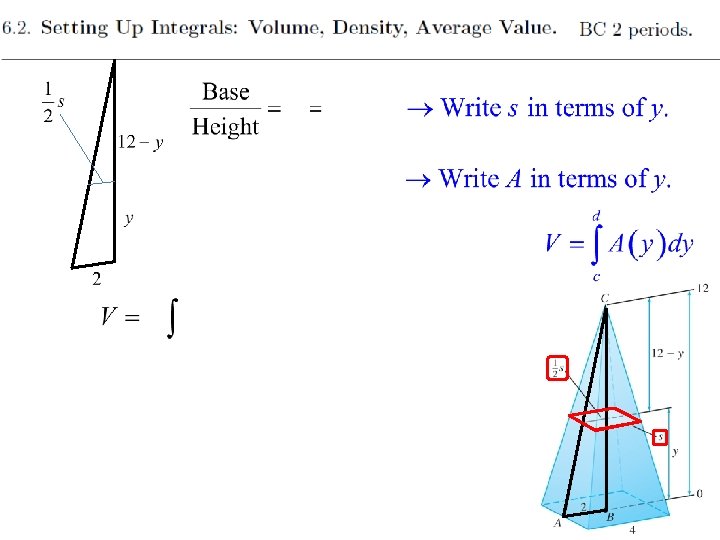
Volume as the Integral of Cross-Sectional Area Let A(y) be the area of the horizontal cross section at height y of a solid body extending from y = c to y = d. Then Volume of a Pyramid Calculate the volume V of a pyramid of height 12 m whose base is a square of side 4 m. We need a formula for the horizontal cross section A(y).

Compute the volume V of the solid, whose base is the region between the parabola y = 4 − x 2 and the x-axis, and whose vertical cross sections perpendicular to the y-axis are semicircles.

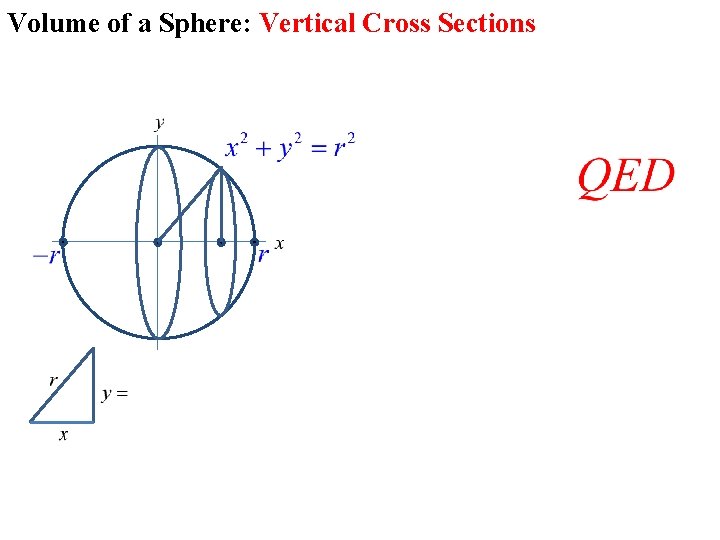
Volume of a Sphere: Vertical Cross Sections Use calculus to prove the formula for volume of a sphere.

CONCEPTUAL INSIGHT Cavalieri’s principle states: Solids with equal cross-sectional areas have equal volume. It is often illustrated convincingly with two stacks of coins includes Cavalieri’s principle, because the volumes V are certainly equal if the crosssectional areas A(y) are equal.

For example, if ℓ = 10 cm and ρ = 9 g/cm

Density Now consider a rod extending along the x-axis from x = a to x = b whose density ρ(x) is a continuous function of x.

Total Mass Find the total mass M of a 2 -m rod of linear density ρ(x) = 1 + x(2 − x) kg/m, where x is the distance from one end of the rod.

In some situations, density is a function of distance to the origin. For example, in the study of urban populations, it might be assumed that the population density ρ(r) (in people per square kilometer) depends only on the distance r from the center of a city. Such a density function is called a radial density function.

Computing Total Population The population in a certain city has radial density function ρ(r) = 15(1 + r 2)− 1/2, where r is the distance from the city center in kilometers and ρ has units of thousands per square kilometer. How many people live in the ring between 10 and 30 km from the city center?

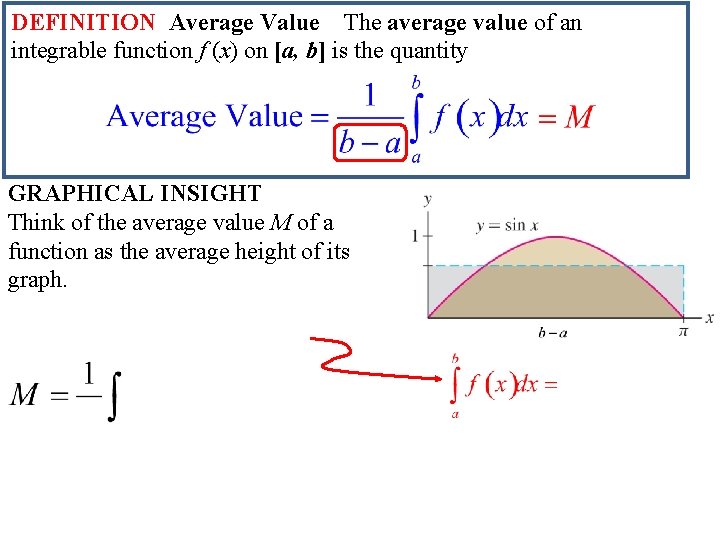
DEFINITION Average Value The average value of an integrable function f (x) on [a, b] is the quantity GRAPHICAL INSIGHT Think of the average value M of a function as the average height of its graph. The region under the graph has the same signed area as the rectangle of height M, because

Vertical Jump of a Bushbaby The bushbaby is a small primate with remarkable jumping ability. Find the average speed during a jump if the initial vertical velocity is υ0 = 600 cm/s. Use Galileo’s formula for the height (in centimeters, where g = 980 cm/s 2).

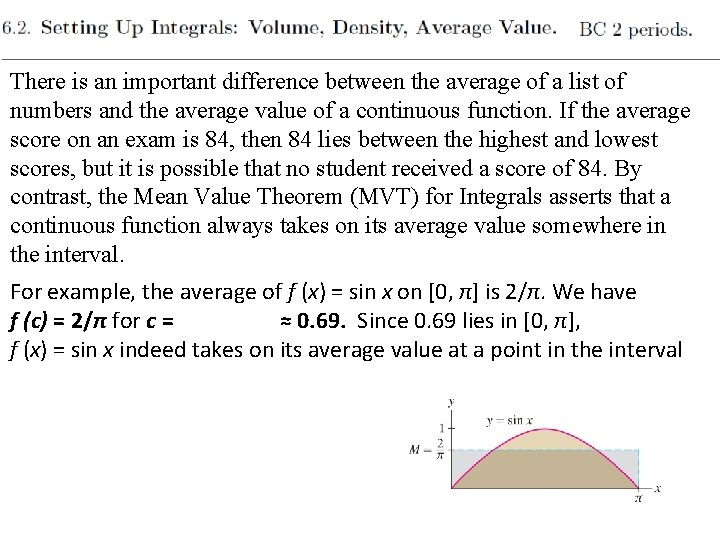
There is an important difference between the average of a list of numbers and the average value of a continuous function. If the average score on an exam is 84, then 84 lies between the highest and lowest scores, but it is possible that no student received a score of 84. By contrast, the Mean Value Theorem (MVT) for Integrals asserts that a continuous function always takes on its average value somewhere in the interval. For example, the average of f (x) = sin x on [0, π] is 2/π. We have f (c) = 2/π for c = sin− 1(2/π) ≈ 0. 69. Since 0. 69 lies in [0, π], f (x) = sin x indeed takes on its average value at a point in the interval

Theorem 1 Mean Value Theorem for Integrals If f (x) is continuous on [a, b], then there exists a value c ε [a, b] such that