Volume of Spheres Unit 3 Geometric Applications of

Volume of Spheres Unit 3: Geometric Applications of Exponents

Volume of Spheres A sphere is the set of points in three dimensions that are a fixed distance from a given point, the center. A plane that intersects a sphere through its center divides the two halves or hemispheres. The edge of a hemisphere is a great circle.

Volume of Spheres The volume of a hemisphere is exactly halfway between the volume of a cone and a cylinder with the same radius r and height equal to r.

Volume of Spheres

Volume of Spheres Find the volume of a sphere with radius 12 cm, both in terms of and to the nearest tenth. Use 3. 14 for . 4 V= r 3 3 = 4 p(12)3 3 Volume of a sphere Substitute 12 for r. = 2304 p cm 3 7, 234. 6 cm 3

Volume of Spheres Find the volume of a sphere with radius 3 m, both in terms of and to the nearest tenth. Use 3. 14 for . 4 V= r 3 3 = 4 p(3)3 3 Volume of a sphere Substitute 3 for r. = 36 p m 3 113. 0 m 3

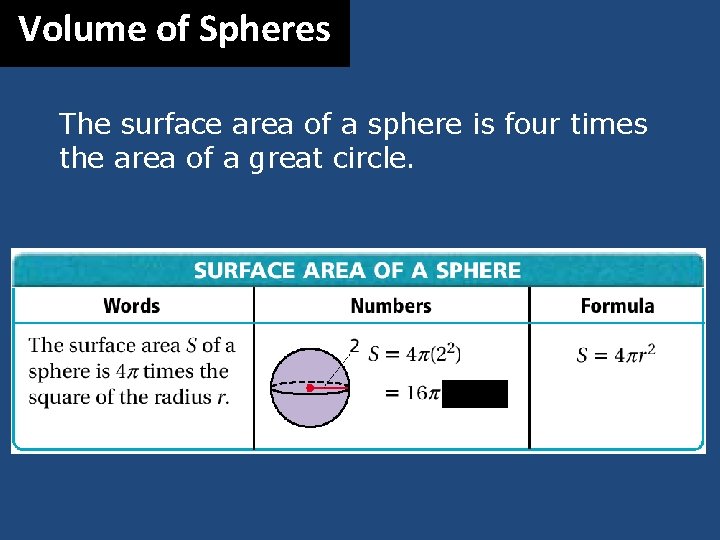
Volume of Spheres The surface area of a sphere is four times the area of a great circle. 50. 3 units 2

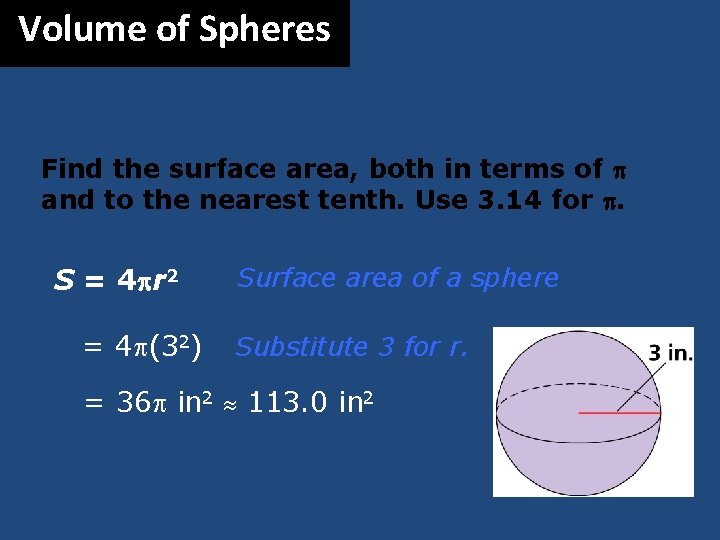
Volume of Spheres Find the surface area, both in terms of and to the nearest tenth. Use 3. 14 for . S = 4 r 2 = 4 p(32) Surface area of a sphere Substitute 3 for r. = 36 p in 2 113. 0 in 2

Volume of Spheres The moon has a radius of 1738 km. Find the surface area, both in terms of and to the nearest tenth. Use 3. 14 for . S = 4 r 2 = 4 p(17382) Surface area of a sphere Substitute 1738 for r. = 12, 082, 576 p km 2 37, 939, 288. 6 km 2 1738 km

Volume of Spheres Compare the volumes and surface areas of a sphere with radius 42 cm with that of a rectangular prism measuring 44 cm 84 cm. Sphere: V = 4 pr 3 = 4 p(423) 3 3 4 22 74, 088 3 7 310, 464 cm 3 Rectangular Prism: V = lwh = (44)(84) = 310, 464 cm 3

Volume of Spheres Sphere: Rectangular Prism: S = 4 pr 2 = 4 p(422) S = 2 lw + 2 lh + 2 wh = 7, 056 p S = 2(44)(84) + 2(84) 22 7, 056 22, 176 cm 2 7 = 28, 896 cm 2 The sphere and the prism have approximately the same volume, but the prism has a larger surface area.

Volume of Spheres Compare the volume and surface area of a sphere with radius 21 mm with that of a rectangular prism measuring 22 42 mm. Sphere: V = 4 pr 3 = 4 p(213) 3 3 4 22 9261 3 7 38, 808 mm 3 Rectangular Prism: V = lwh = (22)(42) = 38, 808 mm 3

Volume of Spheres Sphere: Rectangular Prism: S = 4 pr 2 = 4 p(212) S = 2 lw + 2 lh + 2 wh = 1764 p S = 2(22)(42) + 2(42) 22 1764 5544 mm 2 7 = 7224 mm 2 The sphere and the prism have approximately the same volume, but the prism has a larger surface area.

Volume of Spheres Lesson Quiz: Part I Find the volume of each sphere, both in terms of and to the nearest tenth. Use 3. 14 for . 1. r = 4 ft 85. 3 p ft 3, 267. 8 ft 3 2. d = 6 m 36 p m 3, 113. 0 m 3 Find the surface area of each sphere, both in terms of and to the nearest tenth. Use 3. 14 for . 3. r = 22 in 1936 p in 2, 6079. 0 in 2 4. d = 1. 5 mi 2. 25 p mi 2, 7. 1 mi 2

Volume of Spheres Lesson Quiz: Part II 5. A basketball has a circumference of 29 in. To the nearest cubic inch, what is its volume? 412 in 3