Volume and surface area of a sphere Warm

Volume and surface area of a sphere

Warm Up Find each measurement. 1. the radius of circle M if the diameter is 25 cm 12. 5 cm 2. the circumference of circle X if the radius is 42. 5 85 in. 3. the area of circle T if the diameter is 26 ft 169 ft 2 4. the circumference of circle N if the area is 625 cm 502 cm

Objectives Learn and apply the formula for the volume of a sphere. Learn and apply the formula for the surface area of a sphere.

Vocabulary sphere center of a sphere radius of a sphere hemisphere great circle

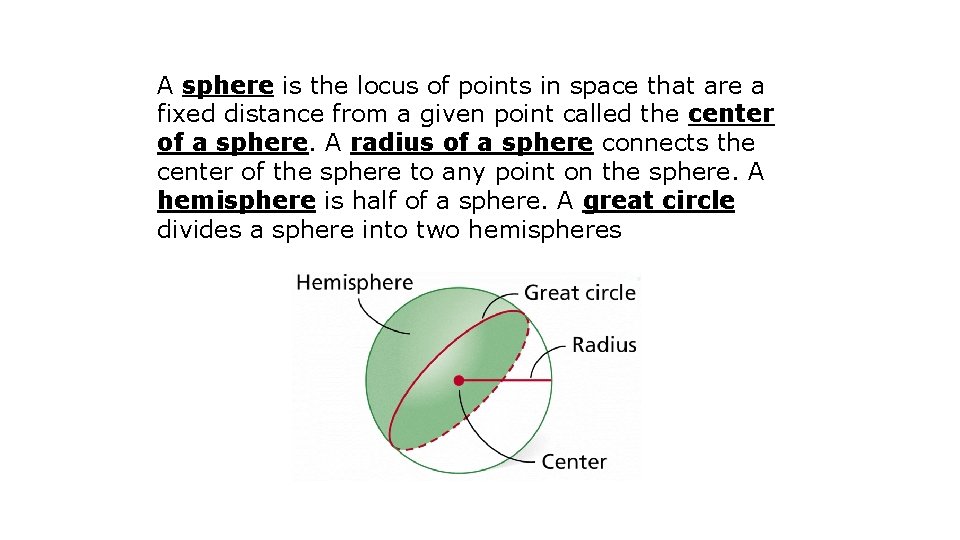
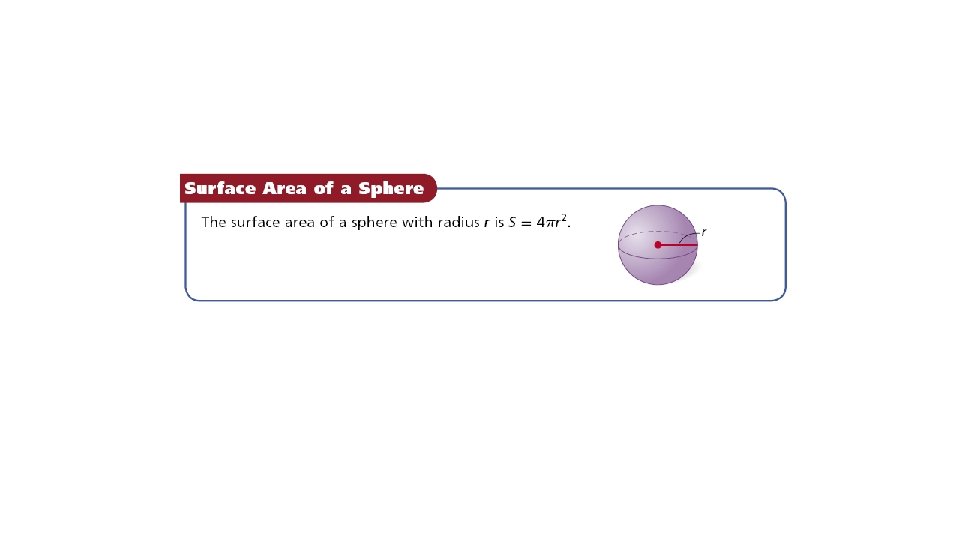
A sphere is the locus of points in space that are a fixed distance from a given point called the center of a sphere. A radius of a sphere connects the center of the sphere to any point on the sphere. A hemisphere is half of a sphere. A great circle divides a sphere into two hemispheres

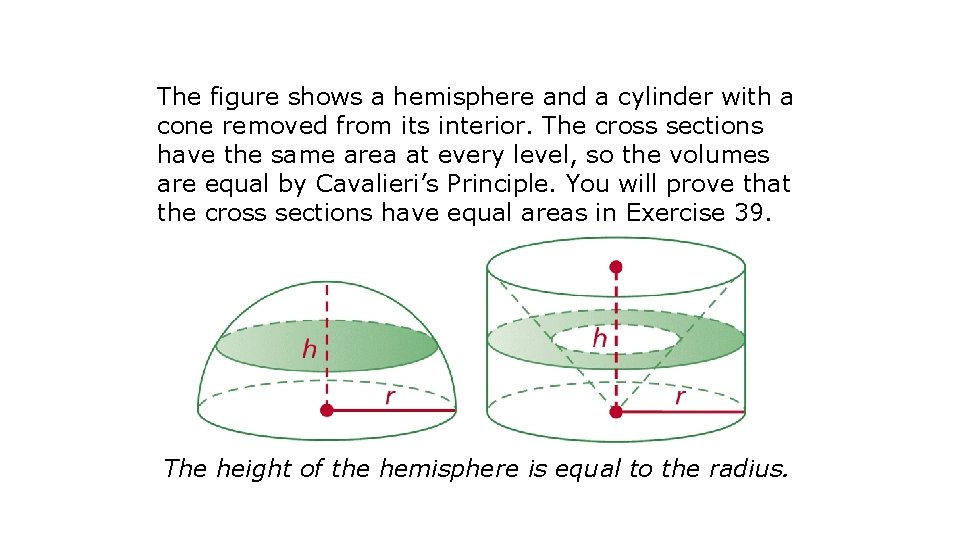
The figure shows a hemisphere and a cylinder with a cone removed from its interior. The cross sections have the same area at every level, so the volumes are equal by Cavalieri’s Principle. You will prove that the cross sections have equal areas in Exercise 39. The height of the hemisphere is equal to the radius.

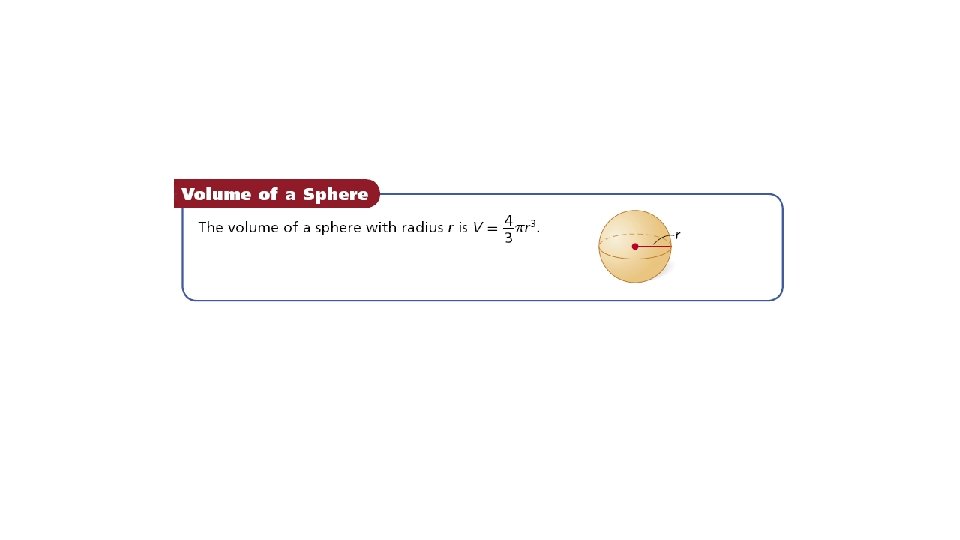
V(hemisphere) = V(cylinder) – V(cone) The volume of a sphere with radius r is twice the volume of the hemisphere, or.

Example 1 A: Finding Volumes of Spheres Find the volume of the sphere. Give your answer in terms of . Volume of a sphere. = 2304 in 3 Simplify.

Example 1 B: Finding Volumes of Spheres Find the diameter of a sphere with volume 36, 000 cm 3. Volume of a sphere. Substitute 36, 000 for V. 27, 000 = r 3 r = 30 Take the cube root of both sides. d = 60 cm d = 2 r

Example 1 C: Finding Volumes of Spheres Find the volume of the hemisphere. Volume of a hemisphere Substitute 15 for r. = 2250 m 3 Simplify.

Check It Out! Example 1 Find the radius of a sphere with volume 2304 ft 3. Volume of a sphere Substitute for V. r = 12 ft Simplify.

Example 2: Sports Application A sporting goods store sells exercise balls in two sizes, standard (22 -in. diameter) and jumbo (34 in. diameter). How many times as great is the volume of a jumbo ball as the volume of a standard ball? jumbo ball: standard ball: A jumbo ball is about 3. 7 times as great in volume as a standard ball.

Check It Out! Example 2 A hummingbird eyeball has a diameter of approximately 0. 6 cm. How many times as great is the volume of a human eyeball as the volume of a hummingbird eyeball? hummingbird: human: The human eyeball is about 72. 3 times as great in volume as a hummingbird eyeball.

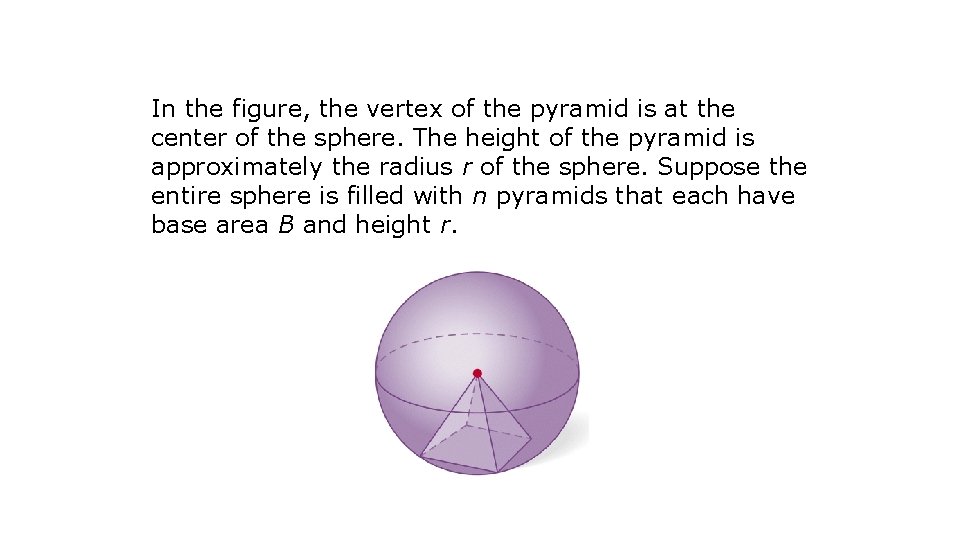
In the figure, the vertex of the pyramid is at the center of the sphere. The height of the pyramid is approximately the radius r of the sphere. Suppose the entire sphere is filled with n pyramids that each have base area B and height r.

4 r 2 ≈ n. B If the pyramids fill the sphere, the total area of the bases is approximately equal to the surface area of the sphere S, so 4 r 2 ≈ S. As the number of pyramids increases, the approximation gets closer to the actual surface area.

Example 3 A: Finding Surface Area of Spheres Find the surface area of a sphere with diameter 76 cm. Give your answers in terms of . S = 4 r 2 Surface area of a sphere S = 4 (38)2 = 5776 cm 2

Example 3 B: Finding Surface Area of Spheres Find the volume of a sphere with surface area 324 in 2. Give your answers in terms of . S = 4 r 2 Surface area of a sphere 324 = 4 r 2 r=9 Substitute 324 for S. Solve for r. Substitute 9 for r. The volume of the sphere is 972 in 2.

Example 3 C: Finding Surface Area of Spheres Find the surface area of a sphere with a great circle that has an area of 49 mi 2. A = r 2 49 = r 2 r=7 Area of a circle Substitute 49 for A. Solve for r. S = 4 r 2 = 4 (7)2 = 196 mi 2 Substitute 7 for r.

Check It Out! Example 3 Find the surface area of the sphere. S = 4 r 2 Surface area of a sphere S = 4 (25)2 Substitute 25 for r. S = 2500 cm 2

Example 4: Exploring Effects of Changing Dimensions The radius of the sphere is multiplied by. Describe the effect on the volume. original dimensions: Notice that by radius multiplied by : . If the radius is multiplied , the volume is multiplied by , or .

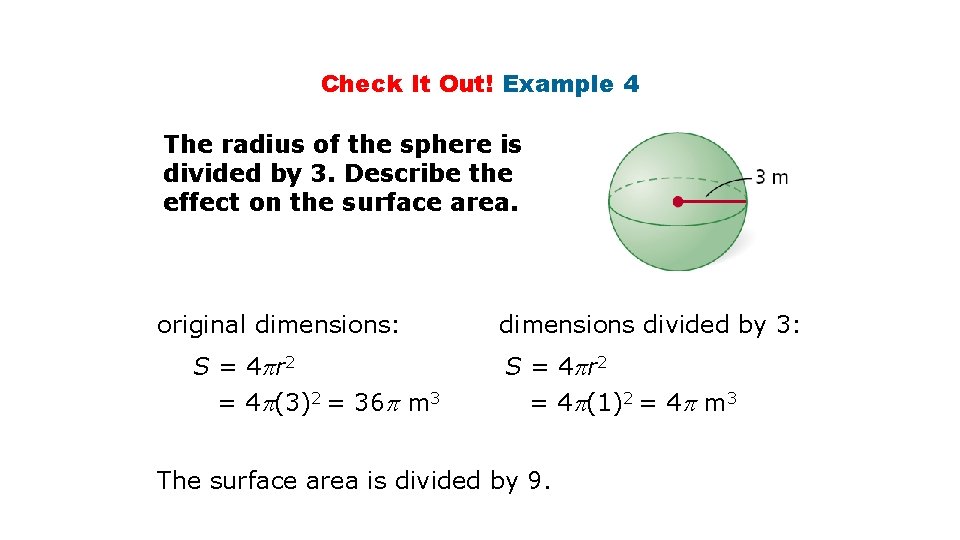
Check It Out! Example 4 The radius of the sphere is divided by 3. Describe the effect on the surface area. original dimensions: S = 4 r 2 = 4 (3)2 = 36 m 3 dimensions divided by 3: S = 4 r 2 = 4 (1)2 = 4 m 3 The surface area is divided by 9.

Example 5: Finding Surface Areas and Volumes of Composite Figures Find the surface area and volume of the composite figure. Give your answer in terms of . Step 1 Find the surface area of the composite figure. The surface area of the composite figure is the sum of the curved surface area of the hemisphere, the lateral area of the cylinder, and the base area of the cylinder.

Example 5 Continued Find the surface area and volume of the composite figure. Give your answer in terms of . L(cylinder) = 2 rh = 2 (6)(9) = 108 in 2 B(cylinder) = r 2 = (6)2 = 36 in 2 The surface area of the composite figure is 72 + 108 + 36 = 216 in 2.

Example 5 Continued Find the surface area and volume of the composite figure. Give your answer in terms of . Step 2 Find the volume of the composite figure. The volume of the composite figure is the sum of the volume of the hemisphere and the volume of the cylinder. The volume of the composite figure is 144 + 324 = 468 in 3.

Check It Out! Example 5 Find the surface area and volume of the composite figure. Step 1 Find the surface area of the composite figure. The surface area of the composite figure is the sum of the curved surface area of the hemisphere, the lateral area of the cylinder, and the base area of the cylinder.

Check It Out! Example 5 Continued Find the surface area and volume of the composite figure. L(cylinder) = 2 rh = 2 (3)(5) = 30 ft 2 B(cylinder) = r 2 = (3)2 = 9 ft 2 The surface area of the composite figure is 18 + 30 + 9 = 57 ft 2.

Check It Out! Example 5 Continued Find the surface area and volume of the composite figure. Step 2 Find the volume of the composite figure. The volume of the composite figure is the volume of the cylinder minus the volume of the hemisphere. V = 45 – 18 = 27 ft 3

Lesson Quiz: Part I Find each measurement. Give your answers in terms of . 1. the volume and surface area V = 36 cm 3; of the sphere S = 36 cm 2 2. the volume and surface area of a sphere with 2 = 288 in 3; great circle area 36 in. V S = 144 in 2 3. the volume and surface area of the hemisphere V = 23, 958 ft 3; S = 3267 ft 2

Lesson Quiz: Part II 4. A sphere has radius 4. If the radius is multiplied by 5, describe what happens to the surface area. The surface area is multiplied by 25. 5. Find the volume and surface area of the composite figure. Give your answer in terms of . V = 522 ft 3; S = 267 ft 2