void mulint a int b int c int




![矩阵相乘的算法 void mul(int a[][], int b[][], int c[][], int n) 执行次数 { Inti, j, 矩阵相乘的算法 void mul(int a[][], int b[][], int c[][], int n) 执行次数 { Inti, j,](http://slidetodoc.com/presentation_image_h/f51214876e5ebc15313f46d34f0a3c41/image-5.jpg)
矩阵相乘的算法 void mul(int a[][], int b[][], int c[][], int n) 执行次数 { Inti, j, k, sum; 1 for(i=0; i<n; i++) n+1 for(j=0; j<n; j++){ n(n+1) sum=0; n 2 for (k=0; k<n; k++) n 2(n+1) sum=sum+a[i][k] * b[k][j]; n 3 c[i][j] = sum; n 2 } } 1. 5 © 2006
![折半查找的算法 int search(int data[], int target, int n) { int i, mid, lower=0, upper=n-1; 折半查找的算法 int search(int data[], int target, int n) { int i, mid, lower=0, upper=n-1;](http://slidetodoc.com/presentation_image_h/f51214876e5ebc15313f46d34f0a3c41/image-6.jpg)
折半查找的算法 int search(int data[], int target, int n) { int i, mid, lower=0, upper=n-1; mid=(lower+upper)/2; while(lower<upper) { if(data[mid]==target) return mid; else if(data[mid] > target) upper = mid - 1; 1. 6 © 2006

折半查找的算法(续) else lower = mid + 1; mid=(lower+upper)/2; } } 1. 7 © 2006

斐波那契数列(递归的程序段) int Fibonacci(int n) { if(n == 0) return 0; else if (n == 1) return 1; else return (Fibonacci(n-1) + Fibonacci(n-2)); } 1. 8 © 2006
斐波那契数列(非递归的 程序段) int Fibonacci(int n) { int prev 1, prev 2, item, i; if (n == 0) return 0; else if (n == 1) return 1; else { 1. 9 prev 2 = 0; prev 1 = 1; for(i=2; i<=n; i++) { item = prev 1 + prev 2; prev 2 = prev 1; prev 1 = item; } return item; } } © 2006
![顺序查找的算法 int search(int data[], int target, int n) { int i; for(i=0; i<n; i++) 顺序查找的算法 int search(int data[], int target, int n) { int i; for(i=0; i<n; i++)](http://slidetodoc.com/presentation_image_h/f51214876e5ebc15313f46d34f0a3c41/image-10.jpg)
顺序查找的算法 int search(int data[], int target, int n) { int i; for(i=0; i<n; i++) if(target == data[i]) return i; } 1. 10 © 2006


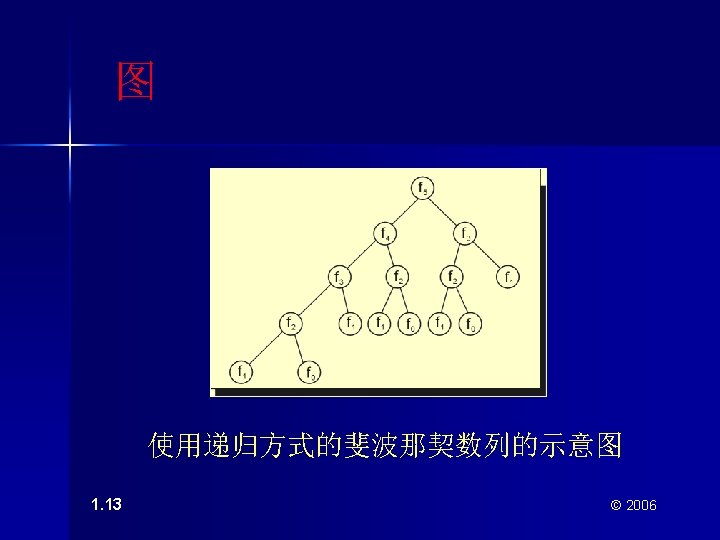
- Slides: 13