VOCALE Um Algoritmo de Identificao de Intervalos Voclicos

VOCALE Um Algoritmo de Identificação de Intervalos Vocálicos no Sinal Acústico de Fala

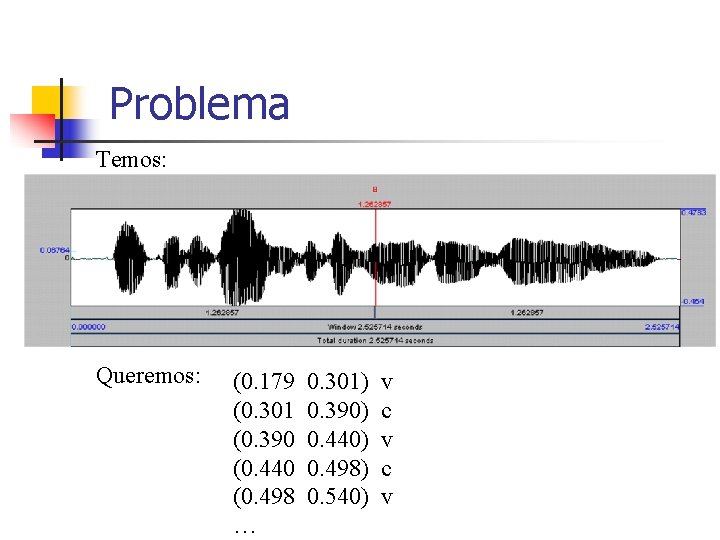
Problema Temos: Queremos: (0. 179 (0. 301 (0. 390 (0. 440 (0. 498 … 0. 301) 0. 390) 0. 440) 0. 498) 0. 540) v c v

Vowel. Cons. Vowel Exemplo de segmentação Marca

Conjectura das classes rítmicas n n n Diversos linguistas conjecturaram que as línguas naturais estavam agrupadas num número finito e pequeno de classes rítmicas ( Lloyd James 1940 , Pike 1945, Abercrombie 1967, etc). Durante meio século não se conseguiu encontrar evidências acústicas que justificassem essa conjectura. Essas evidências aparecem nos artigos pioneiros de Ramus, Nespor e Mehler (1999), eles utilizam estatísticas simples de amostras de sinais acústicos produzidos por falantes das diversas línguas consideradas.

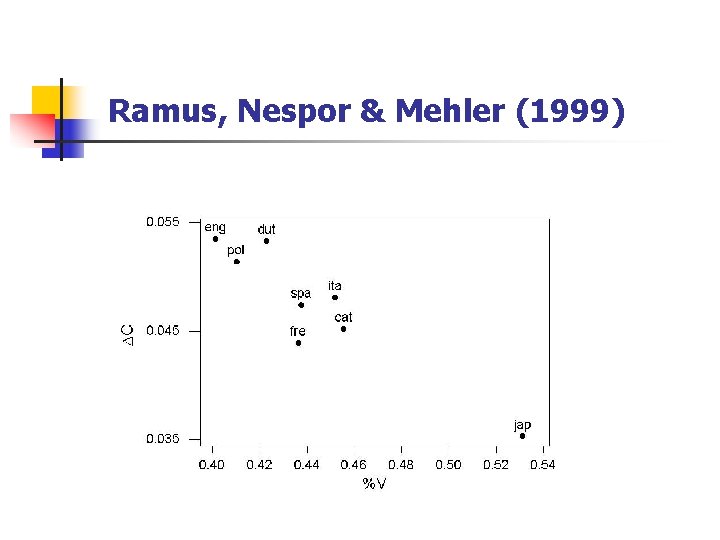
Ramus, Nespor & Mehler (1999) Para um conjunto de oito línguas e 20 frases por língua, eles segmentam as frases em intervalos vocálicos e consonantais e definem: n n %V = proporção de tempo passado em vogais e Delta C = desvio padrão dos intervalos consonantais

Ramus, Nespor & Mehler (1999)

Segmentação manual É feita baseada na seguinte informação: n n n Gráfico do sinal acústico Gráfico do espectrograma Ouvindo a frase

Dificuldades: n n n Leva muito tempo Imprecisões Muito difícil de ser reproduzida

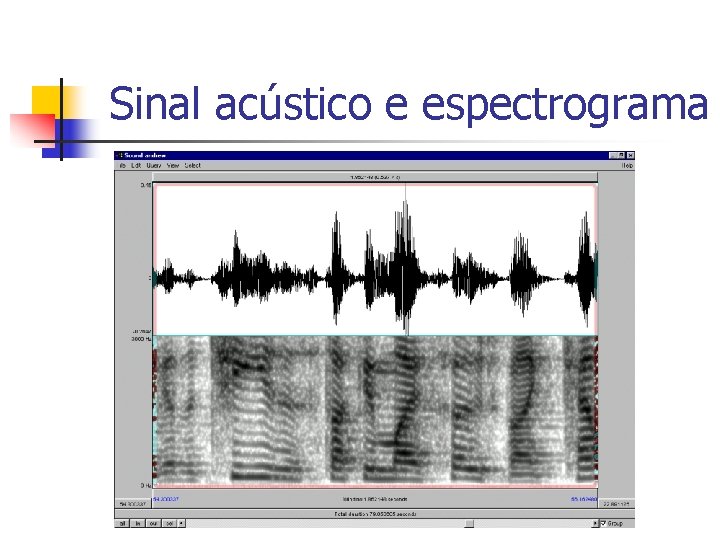
Sinal acústico e espectrograma

Espectro de Fourier Problema: o sinal acústico de fala é não estacionário

Espectrograma

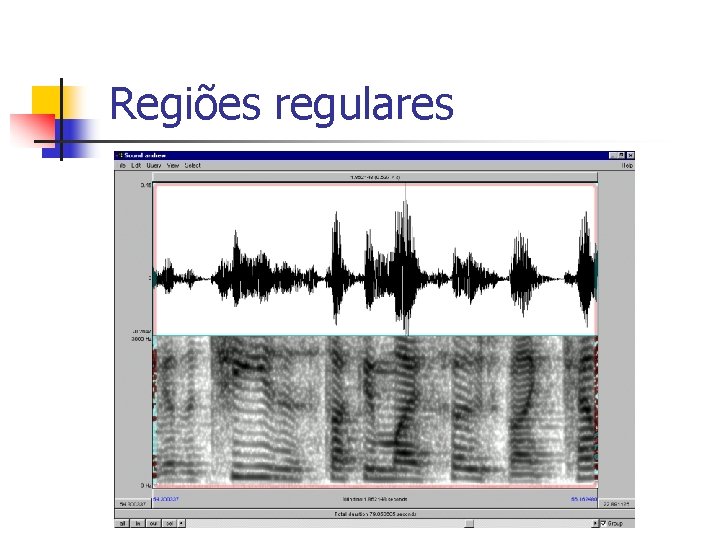
Regiões regulares

Identificando zonas regulares Observação: n Em intervalos vocálicos, tipicamente, p t e pt+1 são “parecidos”. n Em intervalos consonantais, tipicamente, isto não acontece. Exceções: semi-vogais, nasais. . .

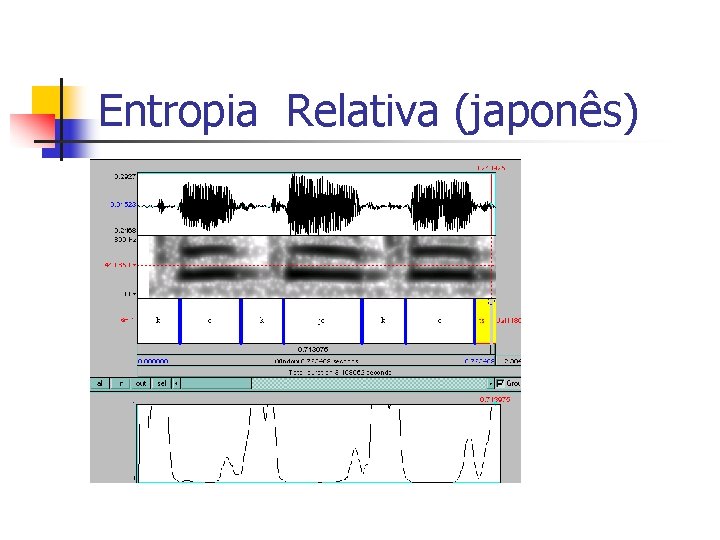
Classificadores(1) n Entropia relativa: n Distância Euclidiana:

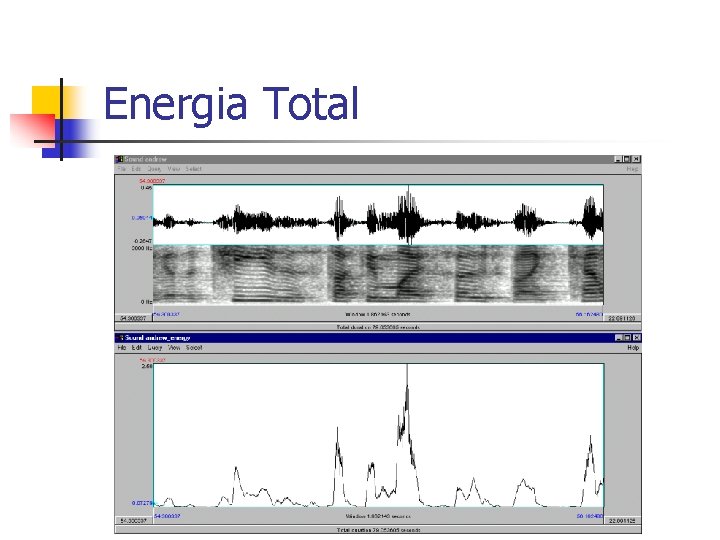
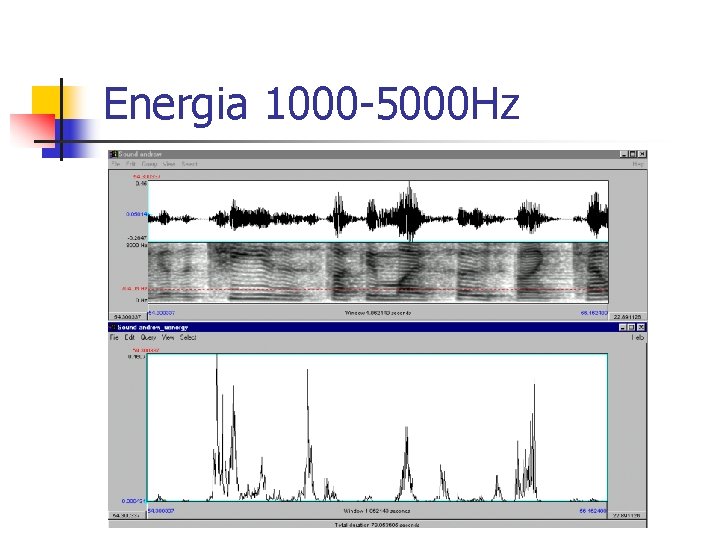
Classificadores(2) n Energia total: n Energia na banda [Fa , Fb]:

Entropia Relativa (japonês)

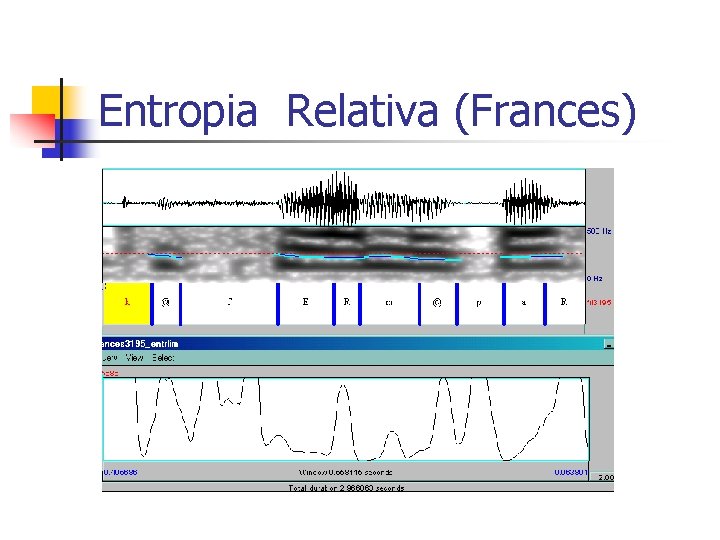
Entropia Relativa (Frances)

Energia Total

Energia 1000 -5000 Hz

Exemplos de Regras de Classificação do P. B. n n n n Entropia relativa baixa Energia total alta Alta energia na banda [1000, 5000] hz alta probabilidade de vogal Entropia relativa baixa alta probabilidade Baixa energia na banda [1000, 5000] hz de consoante (nasal) Entropia relativa alta Alta energia na banda [1000, 5000] hz alta probabilidade de consoante

Segmentação: automática vs manual

Resultados Taxa de erro: n Portugueis Brasileiro: 18% n Ingles Britanico: 24% Consideramos que um erro e produzido quando: n a fronteira não é detectada, ou n a fronteira é colocada a uma distância maior do que 10 ms da marcação manual O algoritmo esta disponivel na rede no endereço: www. ime. usp. br/~tycho/tipal/prosody/vocale/

Problemas: n n n Em alguns casos as regras dependem da língua. As bandas de freqüências a serem utilizadas dependem do sexo do locutor. Há critérios linguísticos que não podem ser expressos com regras simples deste tipo. Exemplos: r retroflexo, semi-vogais, etc.

Exemplo: Português e Inglês

Função de sonoridade Com o objetivo de evitar as ambigüidades na definição de vogal, definimos a função de sonoridade como: S(t) é uma função com valores perto de 1 nas regiões regulares e perto de 0 nas regiões irregulares.

Uma versão automática de RNM

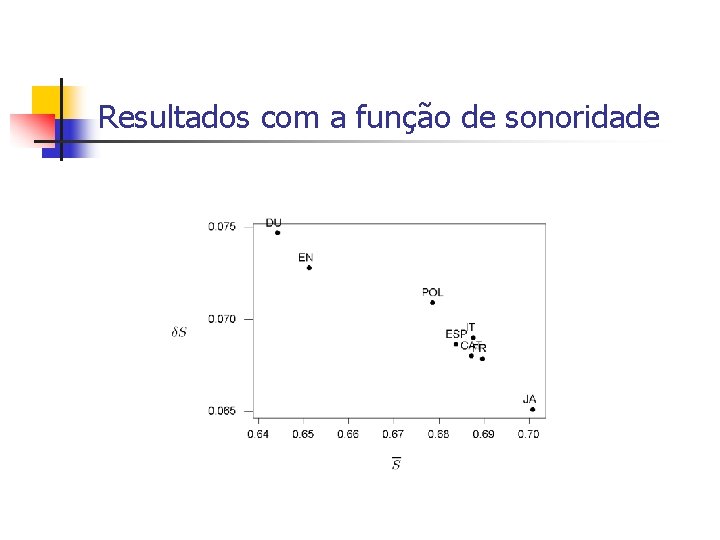
Resultados com a função de sonoridade

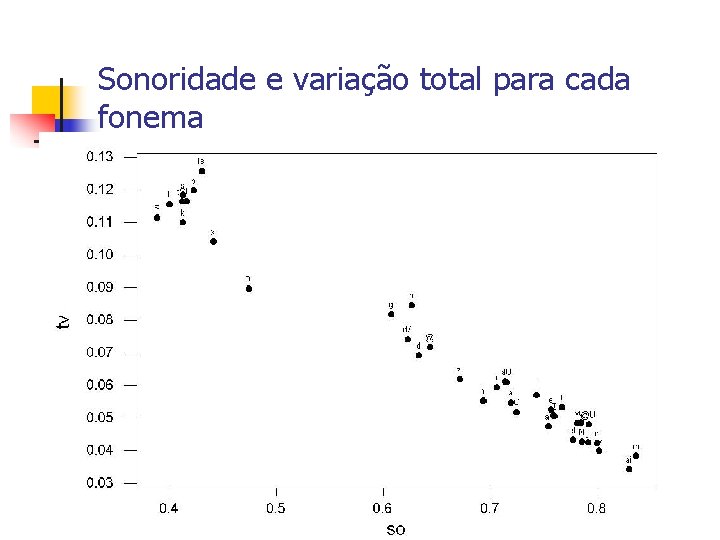
Sonoridade e variação total para cada fonema

Um modelo para a sonoridade

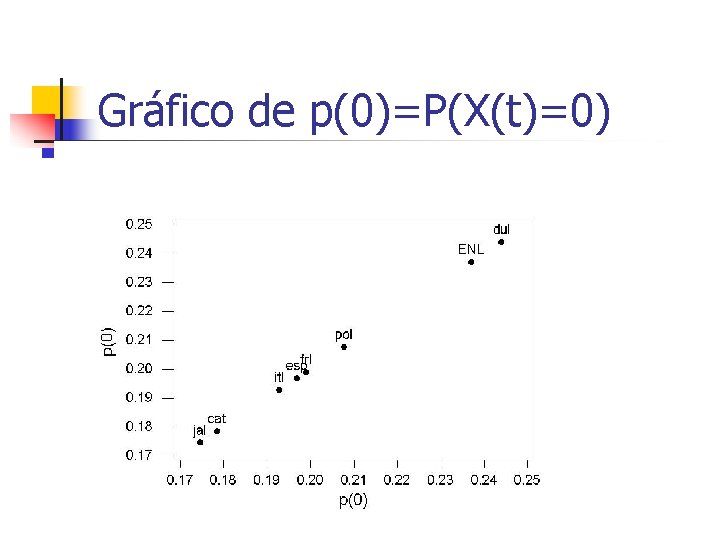
Gráfico de p(0)=P(X(t)=0)