Vocabulary Ratio ratio proportion divide share Can understand

Vocabulary: Ratio ratio proportion divide share

Can understand, use and apply simple ratio to a real problem What is ratio? Ratio is a way of comparing parts of quantities. For example, we may say that to make squash, we need to combine 1 part cordial to 5 parts water. We would say that the ratio of cordial to water is 1: 5. We read this as ‘ 1 to 5’. In ratio, the order of the numbers is very important. In the example above, 1: 5 is the ratio of cordial to water. The ratio of water to cordial is 5: 1.

Can understand, use and apply simple ratio to a real problem What is ratio? In a bag, there are 4 red cubes and 20 blue cubes. Write the ratio of red cubes to blue cubes. The ratio of red cubes to blue cubes is: 4: 20 Remember, the order of the numbers is very important! It would be incorrect to say that the ratio of red cubes to blue cubes is 20: 4.

Can understand, use and apply simple ratio to a real problem Simplifying ratios Ratios can be simplified in the same way as fractions are. Let’s simplify the ratio 4: 20: We cancel down this ratio by finding the largest number that goes into both 4 and 20 (highest common factor). In this case, the highest common factor is 4. We therefore need to divide both 4 and 20 by 4… 4: 20 = 1: 5 Therefore, if we were asked to write the ratio of blue cubes to red cubes, we would write: 20: 4 = 5: 1

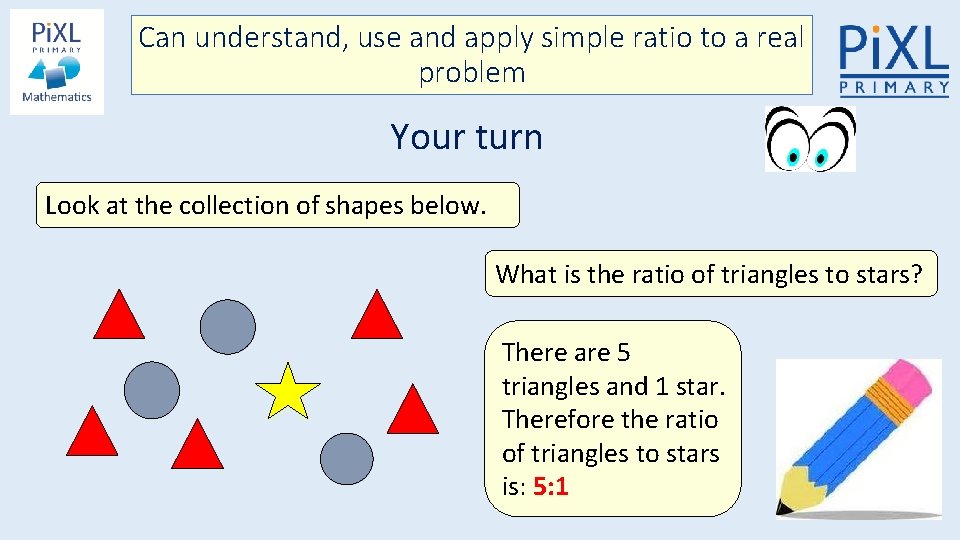
Can understand, use and apply simple ratio to a real problem Your turn Look at the collection of shapes below. What is the ratio of triangles to stars? There are 5 triangles and 1 star. Therefore the ratio of triangles to stars is: 5: 1

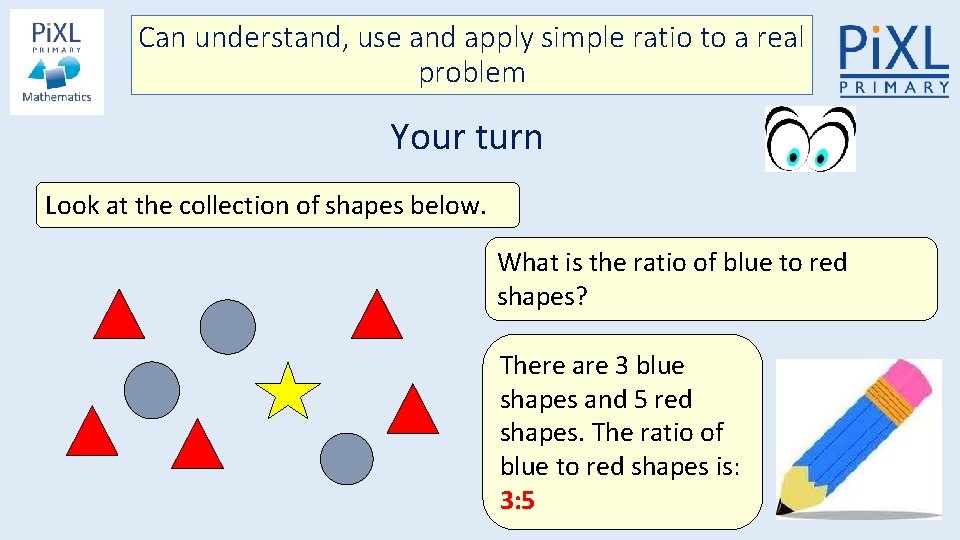
Can understand, use and apply simple ratio to a real problem Your turn Look at the collection of shapes below. What is the ratio of blue to red shapes? There are 3 blue shapes and 5 red shapes. The ratio of blue to red shapes is: 3: 5

Can understand, use and apply simple ratio to a real problem Sometimes you will come across real problems involving ratio. Let’s look at some different methods we can use to work through real life ratio problems…

Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 1 At the gym club, there are 2 girls for every 1 boy. We can say that the ratio of girls to boys is 2: 1. If there are 40 girls at the gym, how many boys are there? We know that for every 2 girls, there is 1 boy. If there are 40 girls, then there must be half the number of boys. Therefore, there are 20 boys. Let’s see how we can also use a diagram to help us understand this problem…

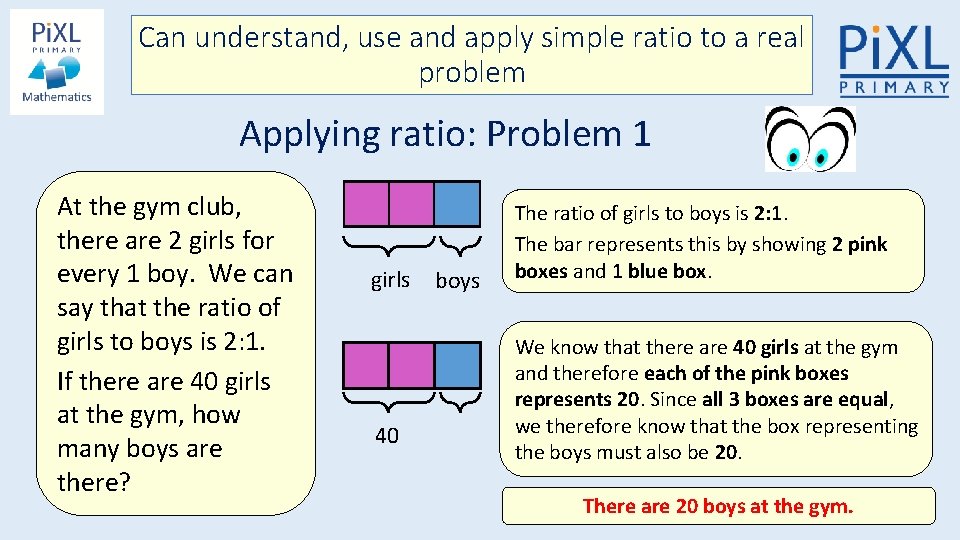
Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 1 At the gym club, there are 2 girls for every 1 boy. We can say that the ratio of girls to boys is 2: 1. If there are 40 girls at the gym, how many boys are there? girls 40 boys The ratio of girls to boys is 2: 1. The bar represents this by showing 2 pink boxes and 1 blue box. We know that there are 40 girls at the gym and therefore each of the pink boxes represents 20. Since all 3 boxes are equal, we therefore know that the box representing the boys must also be 20. There are 20 boys at the gym.

Can understand, use and apply simple ratio to a real problem Your turn In a car park, there are 2 red cars for every blue car. We can say that the ratio of red cars to blue cars is 2: 1. If there are 60 red cars in the car park, how many blue cars are there?

Reasoning The instructions on a packet of cement say: ‘mix cement and sand in the ratio 5: 1’. A builder mixes 5 kg of cement with one bucketful of sand. Could this be correct? Explain your answer.

Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 2 Emma is using the following recipe to make a mango and banana smoothie: Mango and banana smoothie Serves 2 Ingredients 1 Banana 80 g mango 100 g natural yoghurt 125 ml orange and mango juice However, she wants to make the smoothie for 3 people. Calculate how much mango and how much natural yoghurt she will need. Let’s work on this ratio problem together…

Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 2 Emma is using the following recipe to make a mango and banana smoothie: Mango and banana smoothie Serves 2 Ingredients 1 Banana 80 g mango 100 g natural yoghurt 125 ml orange and mango juice The recipe is for 2 people. To find out how much of each ingredient we would need for 3 people, let’s first find out how much we would need for 1 person. The amount needed for 1 person will be half of that needed for 2 people: 1 person: 80 g mango 40 g mango 100 g natural yoghurt 50 g natural yoghurt

Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 2 Emma is using the following recipe to make a mango and banana smoothie: Mango and banana smoothie Serves 2 Ingredients 1 Banana 80 g mango 100 g natural yoghurt 125 ml orange and mango juice 1 person: 40 g mango 50 g natural yoghurt Now we can work out how much is needed for 3 people by multiplying each amount by 3. 3 people: 40 g x 3 mango 50 g x 3 natural yoghurt Therefore, for 3 people Emma would need to use: 120 g mango and 150 g natural yoghurt.

Can understand, use and apply simple ratio to a real problem Your turn Look at the sponge cake recipe below. Traditional sponge cake Serves 4 Ingredients 4 eggs 4 cups of plain flour 8 cups of sugar Robbie wants to make a cake for six people. Calculate how much of each ingredient he will need. Finished? What would he need for ten people?

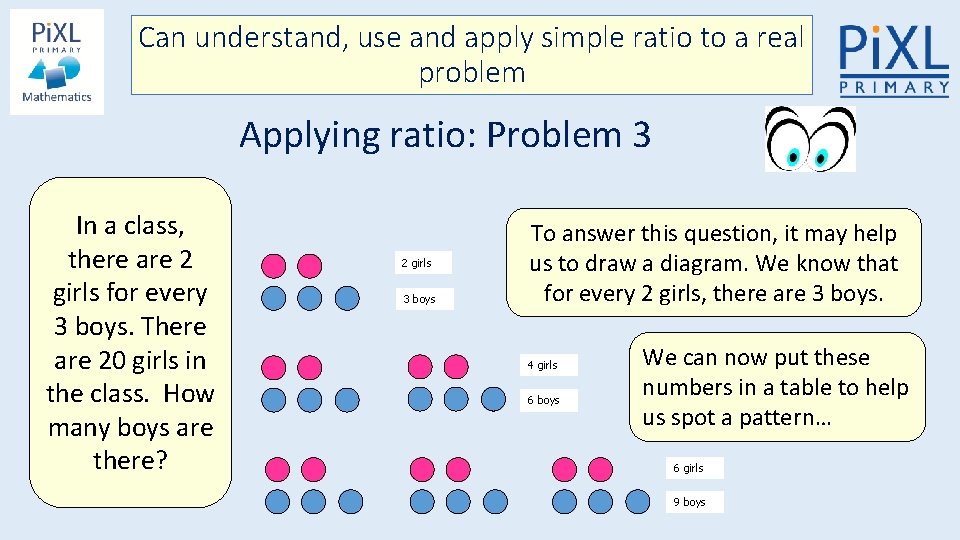
Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 3 In a class, there are 2 girls for every 3 boys. There are 20 girls in the class. How many boys are there? 2 girls 3 boys To answer this question, it may help us to draw a diagram. We know that for every 2 girls, there are 3 boys. 4 girls 6 boys We can now put these numbers in a table to help us spot a pattern… 6 girls 9 boys

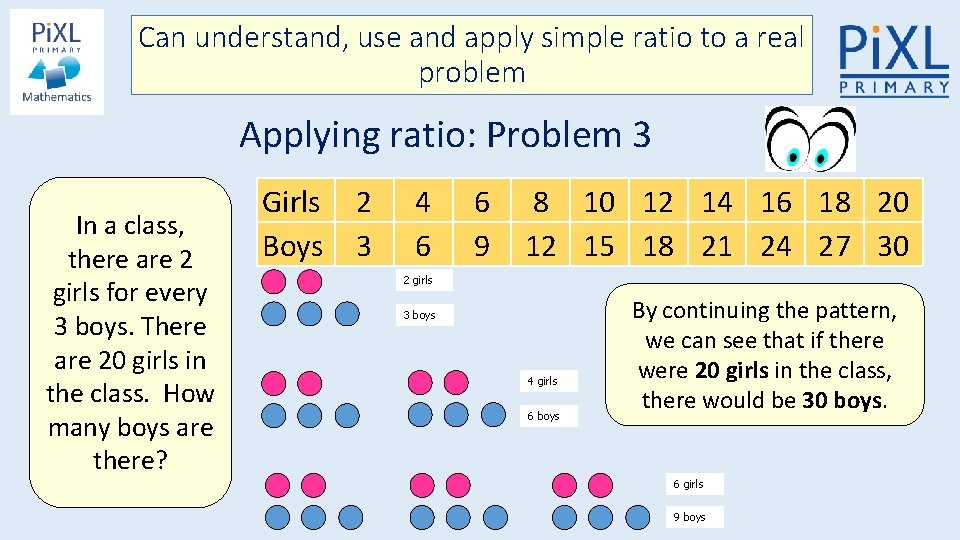
Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 3 In a class, there are 2 girls for every 3 boys. There are 20 girls in the class. How many boys are there? Girls Boys 2 3 4 6 6 9 8 10 12 14 16 18 20 12 15 18 21 24 27 30 2 girls 3 boys 4 girls 6 boys By continuing the pattern, we can see that if there were 20 girls in the class, there would be 30 boys. 6 girls 9 boys

Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 3 In a class, there are 2 girls for every 3 boys. There are 20 girls in the class. How many boys are there? The method we have just used has given us the correct answer but it isn’t very efficient. Let’s consider an alternative method…

Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 3 In a class, there are 2 girls for every 3 boys. There are 20 girls in the class. How many boys are there? We know that for every 2 girls, there are 3 boys. We need to find how many boys there would be if there were 20 girls. 20 is ten times 2 so to find the number of boys, we need to find ten times 3. Number of girls Number of boys 2 20 3 ?

Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 3 In a class, there are 2 girls for every 3 boys. There are 20 girls in the class. How many boys are there? We could also solve the problem using the bar method from our gym problem earlier. The ratio of girls to boys in the class is 2: 3. Let’s draw our bar to represent this. We know that there are 20 girls in the class and therefore each of the 2 boxes in the bar represents 10 girls. We know that all boxes are equal and therefore each of the boxes representing the boys is also 10. Therefore, we can see there are 30 boys in the class. 20 30

Can understand, use and apply simple ratio to a real problem Your turn At the zoo there are 2 penguins for every 5 meerkats. There are 20 penguins. How many meerkats are there? You could solve this problem by drawing a diagram, starting like this: Or you could solve it by drawing a table like this: X? 2 penguins 5 meerkats Number of penguins Number of meerkats 2 20 5 ? X?

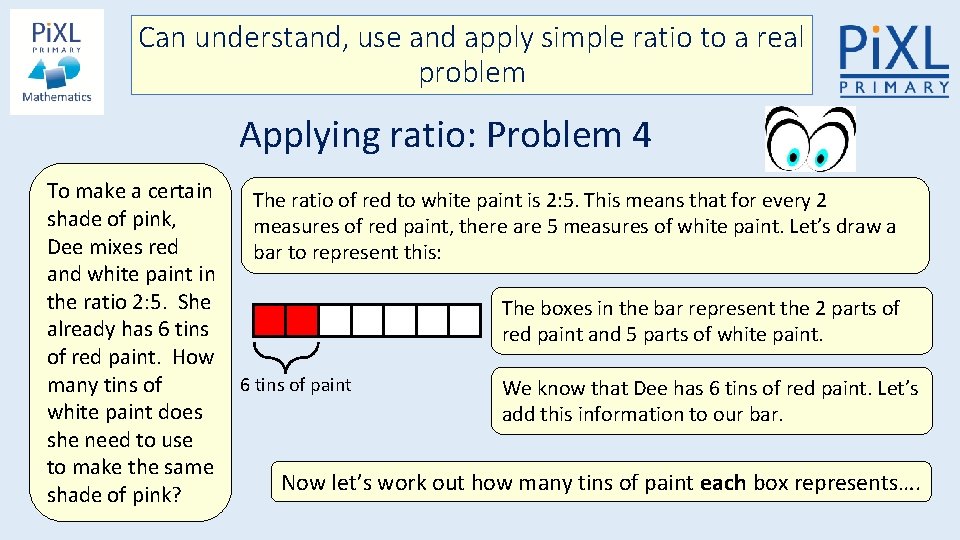
Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 4 To make a certain shade of pink, Dee mixes red and white paint in the ratio 2: 5. She already has 6 tins of red paint. How many tins of white paint does she need to use to make the same shade of pink? The ratio of red to white paint is 2: 5. This means that for every 2 measures of red paint, there are 5 measures of white paint. Let’s draw a bar to represent this: The boxes in the bar represent the 2 parts of red paint and 5 parts of white paint. 6 tins of paint We know that Dee has 6 tins of red paint. Let’s add this information to our bar. Now let’s work out how many tins of paint each box represents….

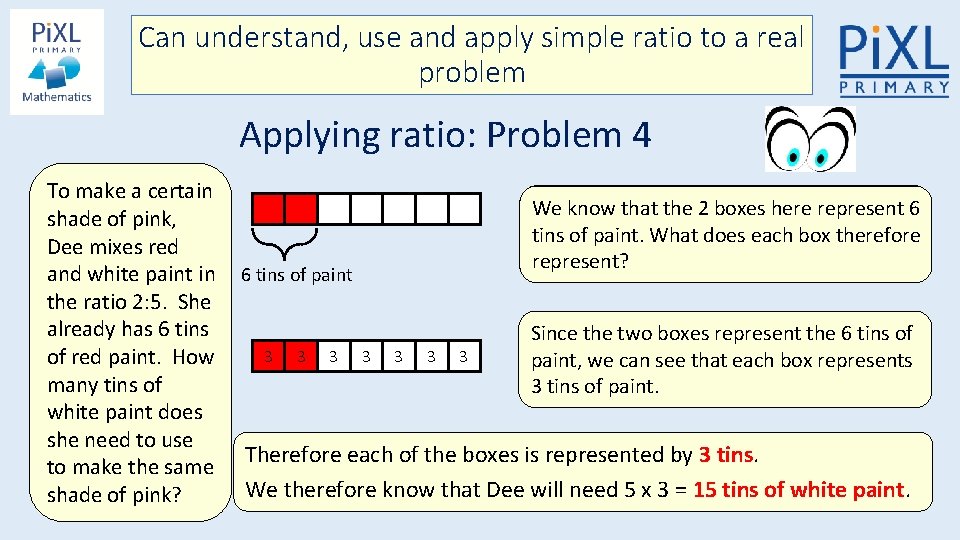
Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 4 To make a certain shade of pink, Dee mixes red and white paint in the ratio 2: 5. She already has 6 tins of red paint. How many tins of white paint does she need to use to make the same shade of pink? We know that the 2 boxes here represent 6 tins of paint. What does each box therefore represent? 6 tins of paint 3 3 3 3 Since the two boxes represent the 6 tins of paint, we can see that each box represents 3 tins of paint. Therefore each of the boxes is represented by 3 tins. We therefore know that Dee will need 5 x 3 = 15 tins of white paint.

Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 4 To make a certain shade of pink, Dee mixes red and white paint in the ratio 2: 5. She already has 6 tins of red paint. How many tins of white paint does she need to use to make the same shade of pink? The method we have just used has given us the correct answer but we could also solve it in a different way. Let’s take a look at an alternative method…

x 3 Can understand, use and apply simple ratio to a real problem Applying ratio: Problem 4 To make a certain shade of pink, Dee mixes red and white paint in the ratio 2: 5. She already has 6 tins of red paint. How many tins of white paint does she need to use have to make the same shade of pink? X 3 If Dee is using 6 tins of red paint we need 3 times as many tins of white (since 6 = 3 x 2). She will therefore need 3 x 5 = 15 tins of white paint. Number of red tins Number of white tins 2 6 5 ? X 3

Can understand, use and apply simple ratio to a real problem Your turn A shade of green paint is produced by mixing 2 litres of blue paint and 4 litres of yellow paint. What is the ratio of blue to yellow paint? How much yellow paint is needed for 10 litres of blue paint? How much green paint in total would be produced if 10 litres of blue paint is used?

Can understand, use and apply simple ratio to a real problem Your turn Two friends divide their £ 150 of lottery winnings in the ratio 1: 2. How much does each get?

Can understand, use and apply simple ratio to a real problem Your turn Kelly spent her savings on books and clothes in the ratio 1: 3. She spent £ 10 on books. How much did she spend on clothes?

Reasoning Convince me that 19: 95 is the same ratio as 1: 5.

A box of building bricks contains three differentcoloured bricks. For every red brick there are four green bricks. For every green brick there are three blue bricks. There are 56 bricks altogether in the box. How many of each colour are there?

Alex is the oldest member of the family by 6 years. Paulo is 12 years older than Harvey. They have a combined age of 69. How old is Alex?

Mo and Nikol are sharing out some coloured pencils in the ratio 2: 6. Mo has 52 fewer pencils than Nikol. How many pencils did they originally have?

In a survey, the ratio of the number of people who preferred toast to those who preferred cereal was 4: 3. 46 more people preferred toast. How many people were surveyed? Effie says, 53 people were surveyed altogether. Is Effie right or wrong? Explain how you know.