Vocabulary Percentages whole per cent numerator denominator Can

Vocabulary: Percentages whole per cent numerator denominator

Can recognise approximate proportions of a whole number using percentages What does ‘percentage’ mean? • • • A percentage represents the number of parts out of 100. The symbol for percentage is %. For example, 76% means 76 out of 100% means 100 out of 100 (or a whole). Percentages can also be written as fractions and decimals.

Can recognise approximate proportions of a whole number using percentages Percentages as fractions and decimals Look at the following percentages written as fractions and decimals:

Can recognise approximate proportions of a whole number using percentages Percentages as fractions and decimals This can be shown on a number line: 0 25% 50% 75% 100%

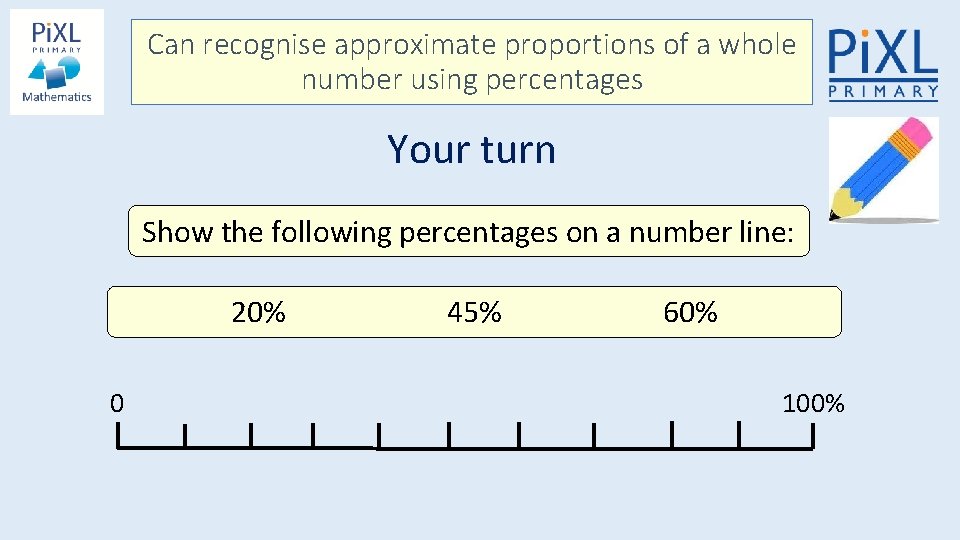
Can recognise approximate proportions of a whole number using percentages Your turn Show the following percentages on a number line: 20% 0 45% 60% 100%

Can recognise approximate proportions of a whole number using percentages Percentages as fractions and decimals We can also show percentages on a hundred square: We can see that 10 squares are shaded out of a total of 100 squares. We can also see that 1 row is shaded out of a total of 10 rows.

Can recognise approximate proportions of a whole number using percentages Percentages as fractions and decimals Let’s work out what percentage of this shape is shaded: We can see that 25 squares are shaded out of a total of 100 squares.

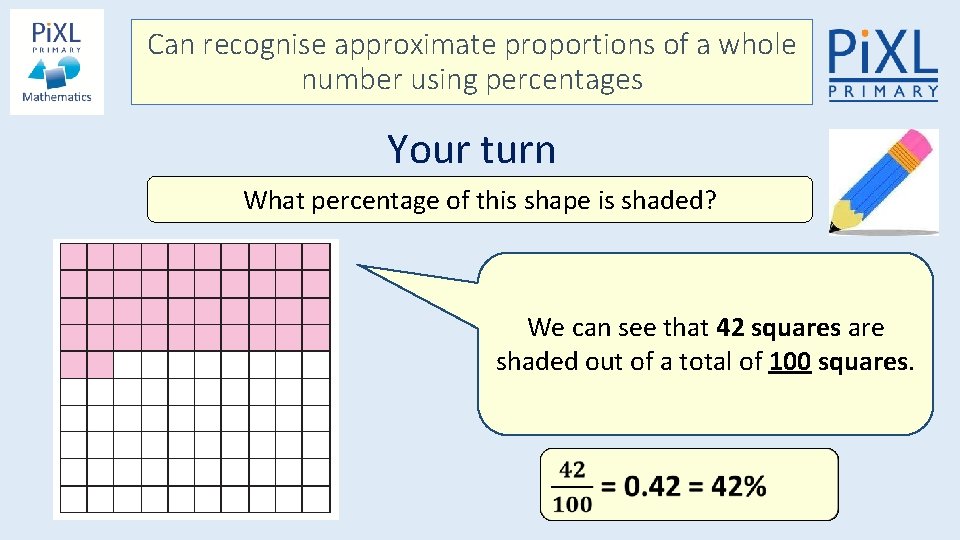
Can recognise approximate proportions of a whole number using percentages Your turn What percentage of this shape is shaded? We can see that 42 squares are shaded out of a total of 100 squares.

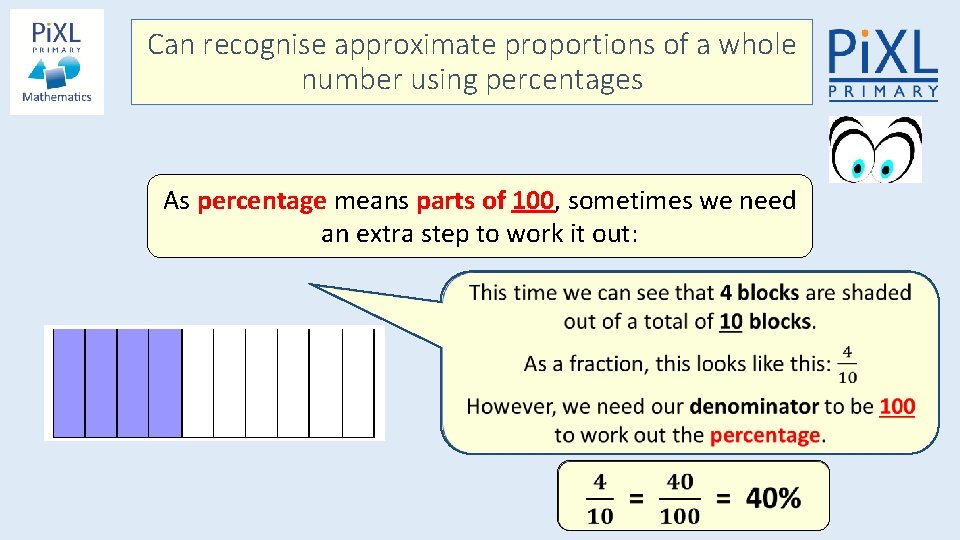
Can recognise approximate proportions of a whole number using percentages As percentage means parts of 100, sometimes we need an extra step to work it out:

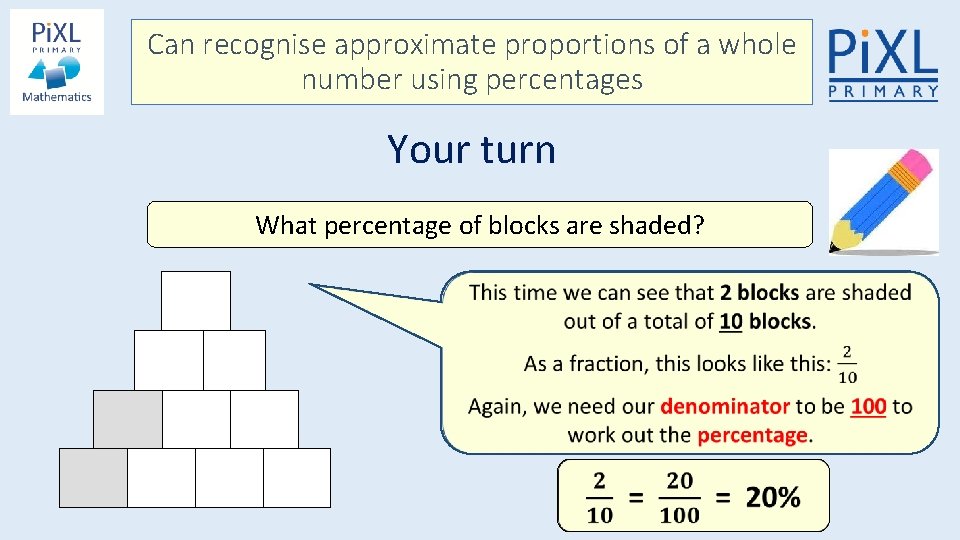
Can recognise approximate proportions of a whole number using percentages Your turn What percentage of blocks are shaded?

Can recognise approximate proportions of a whole number using percentages Common percentages It is important that you know the equivalent fractions to common percentages:

Can recognise approximate proportions of a whole number using percentages Common percentages Once you know these percentages and their fraction equivalents, you can find others. For example:

Can recognise approximate proportions of a whole number using percentages Common percentages Let’s look at another example:

Can recognise approximate proportions of a whole number using percentages Common percentages Often we are asked to find percentages of certain numbers. Sometimes, the easiest way to do that is convert the percentage to a fraction and then work it out. Let’s look at some examples: What is 25% of 12? Therefore, 25% of 12 = 3

Can recognise approximate proportions of a whole number using percentages Common percentages Let’s try this example: What is 50% of 32? Therefore 50% of 32 = 16

Can recognise approximate proportions of a whole number using percentages Common percentages Let’s try this example: What is 75% of 20? Therefore 75% of 20 = 15

Can recognise approximate proportions of a whole number using percentages Your turn Work out the percentages of the following numbers. What is 25% of 60? What is 50% of 96? What is 75% of 80?

Problem Solving A shop has a clothing sale on with 10% off each item – what will each item cost? • T-Shirt: £ 10 • Jumper: £ 12 • Shorts: £ 7 • Coat: £ 34

Problem Solving Increase the following recipe by 50%. Strawberry and banana smoothie Serves 2 Ingredients: 2 Bananas 60 g mango 100 g natural yoghurt 80 ml orange juice

To find 27% of a number, you divide the number by 100 and multiply it by 27. Is this the only method? Can you find three different ways to calculate 27%? Which is the most efficient? Explain your reasoning.

14 pupils in a class wear glasses. 60% of the class do not wear glasses. How many children are in the class? Show your method.

The table shows how the money from a non-school uniform day was spent. £ 312 was unspent. How much money was raised altogether?

The blue rectangle has an area of 36 cm². The red rectangle has an area 25% more than the blue square. What could be the dimensions of the red rectangle?