VLSI Testing and DFT Course Testability Measure What

, , VLSI Testing and DFT Course Testability Measure What do we mean when we say a circuit is testable? Definition: A fault is testable if there exists a well-specified procedure to expose it within a reasonable cost. A circuit is testable if each and every fault in its specified fault set is testable. Testability Measure 1

, , VLSI Testing and DFT Course Keys To Testability 1. Controllability 2. Observability 3. Predictability Testability = Controllability + Observability + Predictability Testability Measure 2

, , VLSI Testing and DFT Course Design for Testability To constrain the design to make test generation and diagnosis easier. Testability Measure 3

, , VLSI Testing and DFT Course Testability (Controllability/Observability) Measures 1. TMEAS [Stephenson & Grason, FTCS, 1976; DAC, 1979] 2. SCOAP [Goldstein, IEEE TCAS-26(9), 1979] 3. TESTSCREEN [Kovijanic 1979] 4. CAMELOT [Bennetts et al. , 1980] 5. VICTOR [Ratiu et al. , ITC, 1982] Testability Measure 4

, , VLSI Testing and DFT Course , Stephenson & Grason s Approach Developed for register-transfer-level (RTL) circuits, but can also be applied at the gate level. The measures are normalized between 0 and 1 to reflect the ease of controlling and observing the internal nodes. Testability Measure 5

, , VLSI Testing and DFT Course , Stephenson & Grason s Approach 1. For each signal line s, we denote the controllability of s as CY(s) and the observability of s as OY(s). 2. The values for the CYs and the OYs of all the signal lines are derived by solving a system of simultaneous equations with the CYs and the OYs as unknowns. The expression used to calculate CY for each output zj is where CTF is the controllability transfer factor of the component. Testability Measure 6

, , VLSI Testing and DFT Course , Stephenson & Grason s Approach Let Nj(0) and Nj(1) be the numbers of input combinations for which zj has value 0 and 1, respectively. Then 0 CTF 1. Each output controllability is assigned the same value. Testability Measure 7

, , VLSI Testing and DFT Course , Stephenson & Grason s Approach The expression used to calculate OY for each input xi is where OTF is the observability transfer factor of the component. Testability Measure 8

, , VLSI Testing and DFT Course , Stephenson & Grason s Approach Let NSi be the numbers of input combinations for which the change of xi results in a change of output. Then NSi also means the number of input combinations that can sensitize a path from xi to the output. The OTF measures the probability that a faulty value at any input will propagate to the outputs. 0 OTF 1 Each input observability is assigned the same value. Testability Measure 9

, , VLSI Testing and DFT Course , Stephenson & Grason s Approach 3. Fanouts: Let s be a fanout stem and k be the number of its branches. Then the CYs of each fanout branch is The observability of the fanout stem s is where bi are fanout branches of s. 4. Sequential components: Sequential components are modeled by adding feedback links around the components that represent internal states. Testability Measure 10

, , VLSI Testing and DFT Course , Goldstein s Approach---SCOAP Sandia Controllability Observability Analysis Program. The measures reflect the difficulty of controlling and observing the internal nodes; higher numbers indicate more difficult to control or observe. The measures are, in a sense, minimum cost values for controlling and observing. Testability Measure 11

, , VLSI Testing and DFT Course , Goldstein s Approach---SCOAP Combinational 1 - and 0 -controllabilities of Y = AND(A, B, C): CC 1(Y) =CC 1(A) + CC 1(B) + CC 1(C) + 1; CC 0(Y) = min{CC 0(A), CC 0(B), CC 0(C)} + 1. The result is incremented by 1 so that the number reflects (in part) the distance to the PIs. Working breadth-first from PIs toward POs, we calculate the CC of the output line of each logic cell as a function of the CCs of its input lines. Testability Measure 12

, , VLSI Testing and DFT Course , Goldstein s Approach---SCOAP The sequential controllability provides an estimate of the number of time frames needed to provide a 0 or 1 at a particular node. For Y=XOR(A, B): CC 0(Y) = min{CC 0(A) +CC 0(B), CC 1(A) + CC 1(B)} + 1 CC 1(Y) = min{CC 0(A) + CC 1(B), CC 1(A) + CC 0(B)} + 1 SC 0(Y) = min{SC 0(A) + SC 0(B), SC 1(A) + SC 1(B)} SC 1(Y) = min{SC 0(A) + SC 1(B), SC 1(A) + SC 0(B)} When computing the sequential controllabilities through combinational circuits, the values are not incremented---no additional time frames needed. Testability Measure 13

, , VLSI Testing and DFT Course , Goldstein s Approach---SCOAP When deriving equations for sequential circuits, SCs are incremented by 1, but CCs are not incremented. Positive edge-triggered DFF with active low reset: CC 0(Q) = min{CC 0(R), CC 1(R) + CC 0(D) + CC 0(C) + CC 1(C)} CC 1(Q) = CC 1(R) + CC 1(D) + CC 0(C) + CC 1(C) SC 0(Q) = min{SC 0(R), SC 1(R) + SC 0(D) + SC 0(C) + SC 1(C)} + 1 SC 1(Q) = SC 1(R) + SC 1(D) + SC 0(C) + SC 1(C) + 1 Testability Measure 14

, , VLSI Testing and DFT Course , Goldstein s Approach---SCOAP Observabilities: CO(P) = CO(N) + CC 1(Q) + CC 1(R) + 1 SO(P) = SO(N) + SC 1(Q) + SC 1(R) Positive edge-triggered DFF with active low reset: CO(R) = CO(Q) + CC 1(Q) + CC 0(R) SO(R) = SO(Q) + SC 1(Q) + SC 0(R) +1 To watch R, then have to watch Q and drive FF to , 1, and then reset it to , 0, . Testability Measure 15

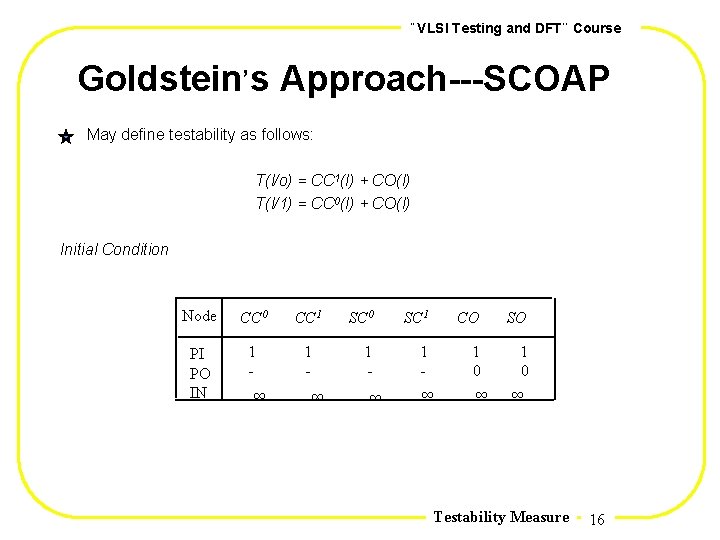
, , VLSI Testing and DFT Course , Goldstein s Approach---SCOAP May define testability as follows: T(l/o) = CC 1(l) + CO(l) T(l/1) = CC 0(l) + CO(l) PI PO IN 1 - CO SO 1 - 1 - 1 0 8 SC 1 8 SC 0 8 CC 1 8 CC 0 8 Node 8 Initial Condition Testability Measure 16

, , VLSI Testing and DFT Course CAMELOT Controllability: CY(output) = CTF(output) x f(CYs(inputs)); controllability transfer factor where N(0) and N(1) are the numbers of input combinations for which the output has value 0 and 1, respectively. Testability Measure 17

, , VLSI Testing and DFT Course CAMELOT CTF(NOT) = 1; CTF(NAND 2) = 1/2; CTF(NAND 3) = 1/4; CTF(ORn) =1/2 n-1 CTF(XORn) = 1. Testability Measure 18

, , VLSI Testing and DFT Course CAMELOT Q+ = [(JQ + KQ)C + QC]PR + P = JQCPR + KQCPR + P Minterms in the final expression is 40; 24 invalid states; 16 common terms in this set of invalid states and the set of minterms derived above. N(1) = 40 16 = 24, and N(0) = (26 - 24) - N(1) = 40 - 24 = 16. CTF = 1 - (24 -16)/40 = 0. 8. By symmetry, the CTF for Q+ is also 0. 8. Testability Measure 19

, , VLSI Testing and DFT Course CAMELOT CY(output) = CTF(output) x f(CYs(input)), where Testability Measure 20

, , VLSI Testing and DFT Course CAMELOT Observability OY(at output) = OTF x OY(at input) x g(CYs(supporting inputs)), Where OTF is the observability transfer factor of the component for the input concerned. Testability Measure 21

, , VLSI Testing and DFT Course CAMELOT where N(SP: I-O) is the total number of distinct sensitive paths from I to O, and N(IP: I-O) is the total number of insensitive paths. Testability Measure 22

, , VLSI Testing and DFT Course CAMELOT OTF(NOT) = 1; OTF(NAND 2) = 1/2 for each input; OTF(NAND 3) = 1/4 for each input (1 PDC & 3 NPDCs); OTF (XORn) = 1 for each input (0 NPDC). Testability Measure 23

, , VLSI Testing and DFT Course CAMELOT Let OY(A-B) denote the observability of node A at node B, then OY(I-O) = OTF(I-O) x OY(I-I) x CY(av), where Testability Measure 24

, , VLSI Testing and DFT Course CAMELOT Fanouts: For a reconvergent fanout, select the shortest I-O path which is to be sensitized (while others are blocked), which is more likely to result in a higher OY. For feedback paths, the strategy is similar to that for reconvergent fanouts with unequal path lengths (i. e. , select the shortest path). Testability Measure 25

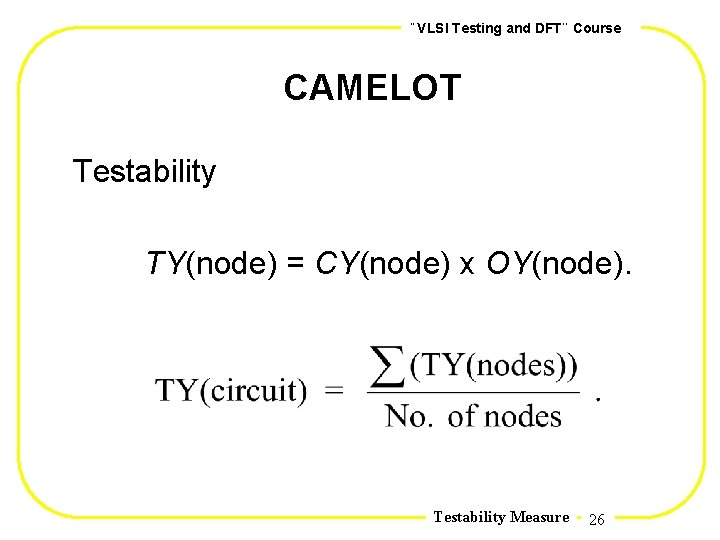
, , VLSI Testing and DFT Course CAMELOT Testability TY(node) = CY(node) x OY(node). Testability Measure 26

, , VLSI Testing and DFT Course CAMELOT() 1. input, check, and initialize circuit; 2. calculate nodal CY values from PIs to POs; 3. calculate nodal OY values from POs to PIs; 4. calculate nodal TY values; 5. calculate TY and interpret the results; Testability Measure 27

, , VLSI Testing and DFT Course Importance of Testability Measures • They can guide the designers to improve the testability of their circuits. • Test generation algorithms using heuristics usually apply some kind of testability measures to their heuristic operations (e. g. , in making search decisions), which greatly speed up the test generation process. Testability Measure 28

, , VLSI Testing and DFT Course Bibliography (1) J. E. Stephenson and J. Grason, , , A testability measure for register transfer level digital circuits, , , in Proc. Int. Symp. Fault tolerant Computing (FTCS), (Pittsburgh, PA), pp. 101 -107, June 1976. (2) J. Grason, , , TMEAS-a testability measurement program, , , in Proc. IEEE/ACM Design Automation Conf. (DAC) , vol. 26, no. 9, pp. 156 -161, 1979. (3) L. H. Goldstein, , , Controllability/observability analysis for digital circuits, , , IEEE Trans. Circuits and Systems, vol. 26, no. 9, pp. 685 -693, Sept. 1979. (4) P. G. Kovijanic, , , Testability analysis, , , in Proc. IEEE Semiconductor Test Conf. , pp. 310 -316, 1979. (5) P. G. Kovijanic, , , Computer-aided testability analysis, , , in Proc. IEEE Autotestcon, pp. 292 -294, 1979. (6) R. G. Bennetts, C. M. Maunder, and G. D. Robinson, , , CAMELOT: a computeraided measure for logic testability, , , IEE Proc. Pt. E, vol. 128, no. 5, pp. 177 -189, 1981. (7) R. G. Bennetts, Design of Testable logic Circuits. Reading, MA: Addison-Wesley, 1984. Testability Measure 29

, , VLSI Testing and DFT Course Bibliography (8) I. M. Ratiu, A. Sangiovanni-Vincentelli, and D. O. Pederson, , , VICTOR: a fast VLSI testability analysis program, , , in Proc. Int. Test Conf. (ITC), (Philadelphia, PA), pp. 397 -401, Nov. 1982. (9) W. C. Berg and R. C. Hess, , , COMET : a testability analysis and design modification package, , , in Proc. Int. Test Conf. (ITC), (Philadelphia, PA), pp. 364 -378, Nov. 1982. Testability Measure 30