VLSI Signal Processing VLSI SIGNAL PROCESSING OBJECTIVES To

VLSI Signal Processing

VLSI SIGNAL PROCESSING OBJECTIVES �To understand the various VLSI architectures for digital signal processing. �To know the techniques of critical path and algorithmic strength reduction in the filter structures. �To study the performance parameters, viz. area, speed and power. OUTCOMES �To be able to design architectures for DSP algorithms. �To be able to optimize design in terms of area, speed and power. �To be able to incorporate pipeline based architectures in the design. �To be able to carry out HDL simulation of various DSP algorithms. 3

Applications 4

Need for VLSI DSP System Processors for DSP system • General Purpose Microprocessors/Microcontrollers • General Purpose DSPs • Custom Processors in VLSI- FPGA, ASIC Real time throughput • Sampling rates from 20 KHz to 500 MHz • Present sample is to be processed before the arrival of the next sample; if not buffered • Processing rate upto 100 GOPs/sec is required

Need for VLSI DSP system …. Data Driven property • Systems are synchronized by data and not by clock • Asynchronous operation possible Reduced size • For portable and mobile applications • High density circuits available - 90 Mn. Tr/cm 2 • Increases according to Moore’s Law • Submicron fabrication technology feasible 0. 07µm to 22 nm 6

Typical DSP Algorithms Filtering • FIR, IIR filters • • • y(n) = ∑ ak y(n-k) + ∑ bk x(n-k) k k With (Recursive) and without feedback Convolution and Correlation y(n) = ∑ x(k) h (n-k) y(n) = ∑ a(k) x (n+k) n= 1 to ∞ Non-terminating programs – Execute the same code repetitively • Adaptive Filters –LMS Algorithm 7

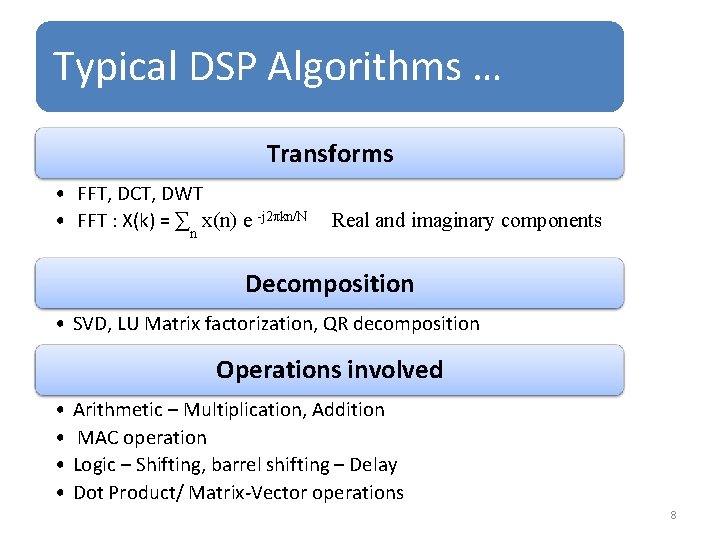
Typical DSP Algorithms … Transforms • FFT, DCT, DWT • FFT : X(k) = ∑n x(n) e -j 2πkn/N Real and imaginary components Decomposition • SVD, LU Matrix factorization, QR decomposition Operations involved • • Arithmetic – Multiplication, Addition MAC operation Logic – Shifting, barrel shifting – Delay Dot Product/ Matrix-Vector operations 8

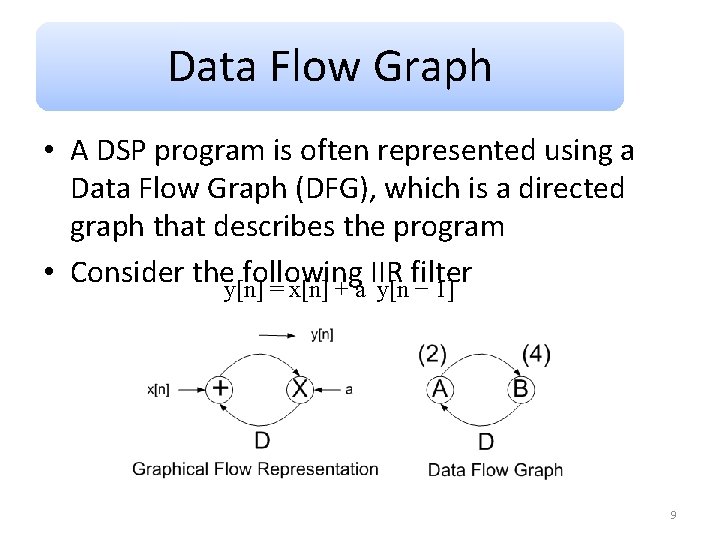
Data Flow Graph • A DSP program is often represented using a Data Flow Graph (DFG), which is a directed graph that describes the program • Consider they[n] following IIR filter = x[n] + a y[n − 1] 9

Data Flow Graph …. In the DFG, nodes represent the tasks or computations (Multiplication/Addition) Each task is associated with its corresponding execution time The edges represent the communications between the nodes e. g. A → B Associated with each edge is a non-negative number representing the delay An iteration of the node is the execution of the node, exactly once 10

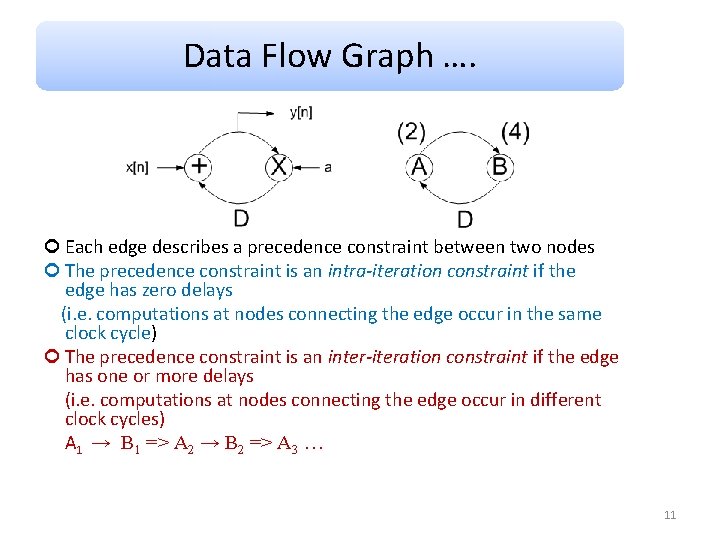
Data Flow Graph …. Each edge describes a precedence constraint between two nodes The precedence constraint is an intra-iteration constraint if the edge has zero delays (i. e. computations at nodes connecting the edge occur in the same clock cycle) The precedence constraint is an inter-iteration constraint if the edge has one or more delays (i. e. computations at nodes connecting the edge occur in different clock cycles) A 1 → B 1 => A 2 → B 2 => A 3 … 11

• Speed – Highest frequency of operation • Area – minimum area required • Power – minimum power to operate • All three may not be satisfied simultaneously 12

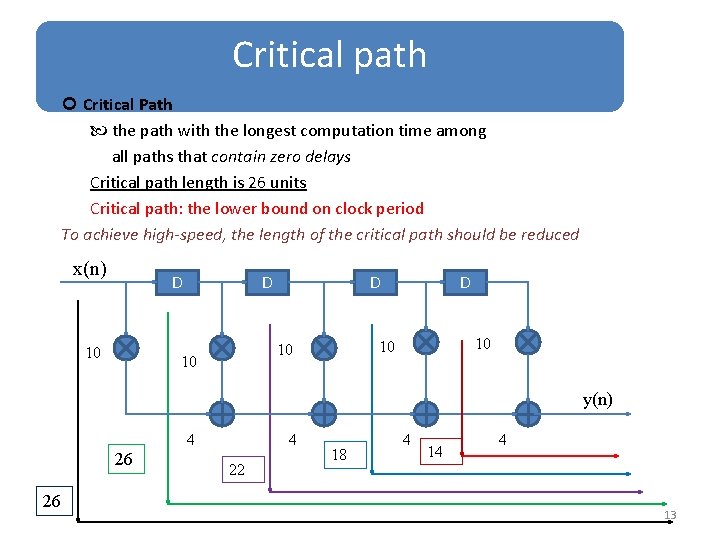
Critical path Critical Path the path with the longest computation time among all paths that contain zero delays Critical path length is 26 units Critical path: the lower bound on clock period To achieve high-speed, the length of the critical path should be reduced x(n) D 10 D D 10 10 D y(n) 4 26 26 4 22 18 4 14 4 13