VLSI Signal Processing Dr Elwin Chandra Monie Department

VLSI Signal Processing Dr. Elwin Chandra Monie Department of ECE, RMK Engineering College

256 K MEMORY CHIP 2 Dept. of ECE, RMK Engineering College

APPLICATIONS 3 Dept. of ECE, R M K Engineering College

SYLLABUS Anna University syllabus for VL 9253 VLSI Signal processing Text Keshab K. Parhi, ‘VLSI Digital Signal Processing Systems, Design and implementation’, Wiley India Pvt. Ltd. , 2009 4 Dept. of ECE, RMK Engineering College

Need for VLSI DSP System Processors for DSP system • General Purpose Microprocessors/Microcontrollers • General Purpose DSPs • Custom Processors in VLSI- FPGA, ASIC Real time throughput • Sampling rates from 20 KHz to 500 MHz • Present sample is to be processed before the arrival of the next sample; if not buffered • Processing rate upto 100 GOPs/sec is required Dept. of ECE, R M K Engineering College 5

Need for VLSI DSP system …. Data Driven property • Systems are synchronized by data and not by clock • Asynchronous operation possible Reduced size • • For portable and mobile applications High density circuits available - 90 Mn. Tr/cm 2 Increases according to Moore’s Law Submicron fabrication technology feasible 0. 07µm 6 Dept. of ECE, R M K Engineering College

Typical DSP Algorithms Filtering • FIR, IIR filters • • • y(n) = ∑ ak y(n-k) + ∑ bk x(n-k) k k With (Recursive) and without feedback Convolution and Correlation y(n) = ∑ x(k) h (n-k) y(n) = ∑ a(k) x (n+k) n= 1 to ∞ Non-terminating programs – Execute the same code repetitively • Adaptive Filters –LMS Algorithm 7 Dept. of ECE, R M K Engineering College

Typical DSP Algorithms … Transforms • FFT, DCT, DWT • FFT : X(k) = ∑n x(n) e -j 2πkn/N components Real and imaginary Decomposition • SVD, LU Matrix factorization, QR decomposition Operations involved • • Arithmetic – Multiplication, Addition MAC operation Logic – Shifting, barrel shifiting – Delay Dot Product/ Matrix-Vector operations 8 Dept. of ECE, R M K Engineering College

Data Flow Graph A DSP program is often represented using a Data Flow Graph (DFG), which is a directed graph that describes the program Consider the following IIR filter y[n] = x[n] + a y[n − 1] 9 Dept. of ECE, RMK Engineering College

Data Flow Graph …. In the DFG, nodes represent the tasks or computations (Multiplication/Addition) Each task is associated with its corresponding execution time The edges represent the communications between the nodes A → B Associated with each edge is a non-negative number representing the delay An iteration of the node is the execution of the node, exactly once 10 Dept. of ECE, RMK Engineering College

Data Flow Graph …. Each edge describes a precedence constraint between two nodes The precedence constraint is an intra-iteration constraint if the edge has zero delays (i. e. computations at nodes connecting the edge occur in the same clock cycle) The precedence constraint is an inter-iteration constraint if the edge has one or more delays (i. e. computations at nodes connecting the edge occur in different clock cycles) A 1 → B 1 => A 2 → B 2 => A 3 … 11 Dept. of ECE, RMK Engineering College

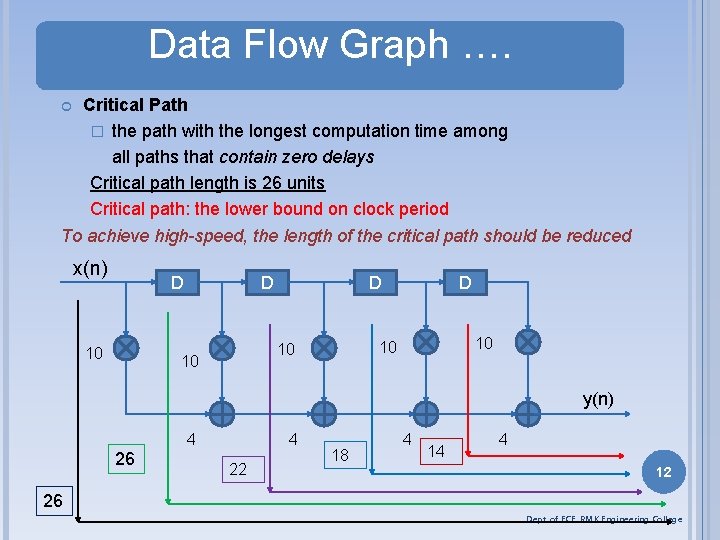
Data Flow Graph …. Critical Path � the path with the longest computation time among all paths that contain zero delays Critical path length is 26 units Critical path: the lower bound on clock period To achieve high-speed, the length of the critical path should be reduced x(n) D 10 D D 10 10 D y(n) 4 26 4 22 18 4 14 4 12 26 Dept. of ECE, RMK Engineering College

Loop Bound A recursive DFG has one or more loops A loop bound for the L-th loop is defined as t. L / w. L � t. L is the loop computation time � w. L is the number of delays in the loop Iteration bound T∞ � Iteration bound is the maximum loop bound of all loops in the DFG � The loop that gives the iteration bound is called the critical loop The iteration bound determines the minimum critical path of a recursive system represented by that DFG structure! In other words, no matter how you pipeline or retime the DFG, you cannot get a circuit with lower critical path than the iteration bound! 13 Dept. of ECE, RMK Engineering College

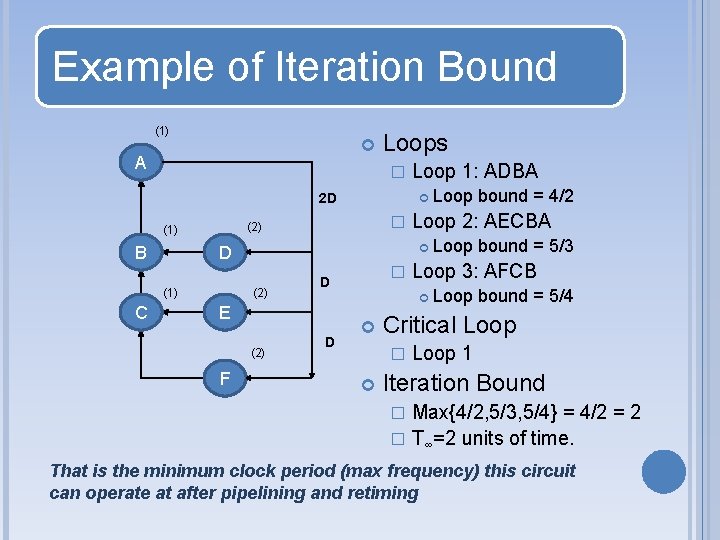
Example of Iteration Bound (1) A Loops � 2 D B � (2) F D Loop bound = 5/4 Critical Loop � Loop bound = 5/3 Loop 3: AFCB E (2) � D Loop bound = 4/2 Loop 2: AECBA D (1) C (2) (1) Loop 1: ADBA Loop 1 Iteration Bound Max{4/2, 5/3, 5/4} = 4/2 = 2 � T∞=2 units of time. � That is the minimum clock period (max frequency) this circuit can operate at after pipelining and retiming

Longest path matrix algorithm-1 Let d be the number of delays in DFG. Define K = [1, 2, · · · , d] Form the matrix L(1) as follows L(1)i, j = d i → dj max t if at least one path exists q q -1 if no such path exists where max tqd i → dj is the maximum of the longest computation time between delay element di to delay element dj 15 Dept. of ECE, RMK Engineering College

Longest path matrix algorithm-2 Compute the successive matrices L(m+1)i, j = max ( -1, L(1)i, k + L(m)k, j ) k S in which Si, j = { k K |(li, j -1) & (lk, j -1)} The iteration bound is computed from T∞ = max i, m K L(m)i, i -----m 16 Dept. of ECE, RMK Engineering College

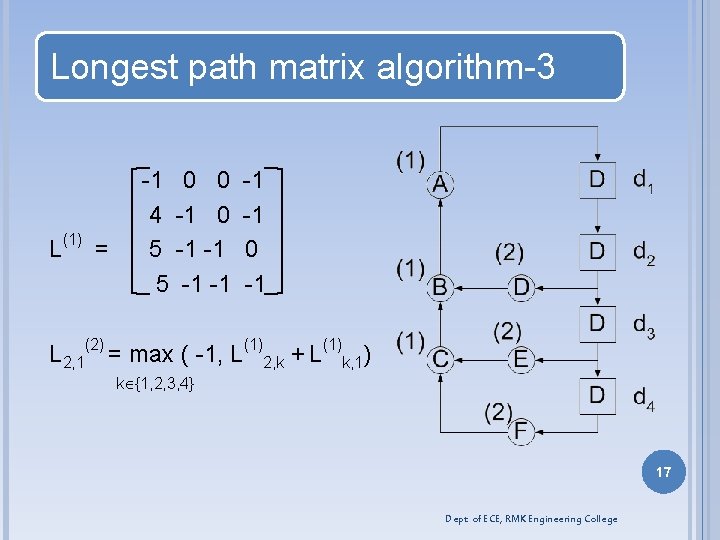
Longest path matrix algorithm-3 L(1) = -1 0 0 4 -1 0 5 -1 -1 0 -1 L 2, 1(2) = max ( -1, L(1)2, k + L(1)k, 1) k {1, 2, 3, 4} 17 Dept. of ECE, RMK Engineering College

LONGEST PATH MATRIX ALGORITHM-4 L 2, 1(2) = max( -1, L(1)2, k + L(1)k, 1) k {1, 2, 3, 4} = max( -1, 0+5) = 5 L 2, 2(2) = max( -1, L(1)2, k + L(1)k, 2) k {1, 2, 3, 4} = max( -1, 4+0 ) = 4 L 2, 3(2) = max( -1, L(1)2, k + L(1)k, 3) k {1, 2, 3, 4} = max(-1) = -1 L 2, 4(2) = max ( -1, L(1)2, 4 + L(1)k, 4) k {1, 2, 3, 4} = max(-1, 0+0) = 0 18 Dept. of ECE, RMK Engineering College

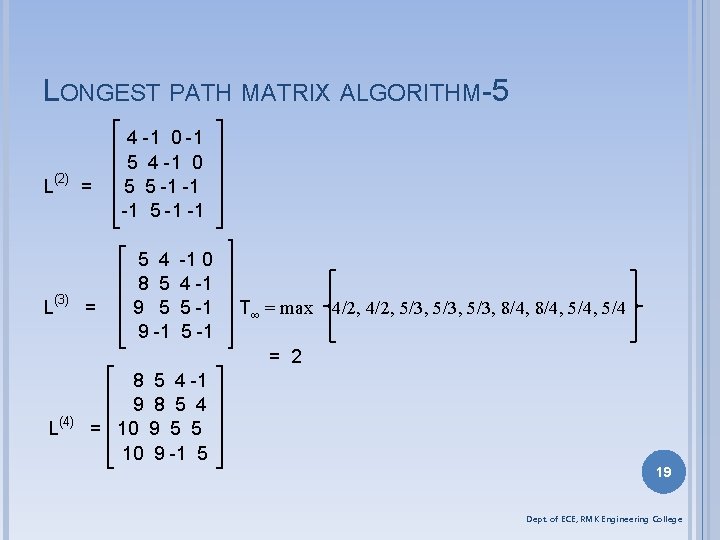
LONGEST PATH MATRIX ALGORITHM-5 L(2) = L(3) = 4 -1 0 -1 5 4 -1 0 5 5 -1 -1 -1 5 4 8 5 9 -1 -1 0 4 -1 5 -1 T∞ = max 4/2, 5/3, 8/4, 5/4 = 2 L(4) 8 5 4 -1 9 8 5 4 = 10 9 5 5 10 9 -1 5 19 Dept. of ECE, RMK Engineering College

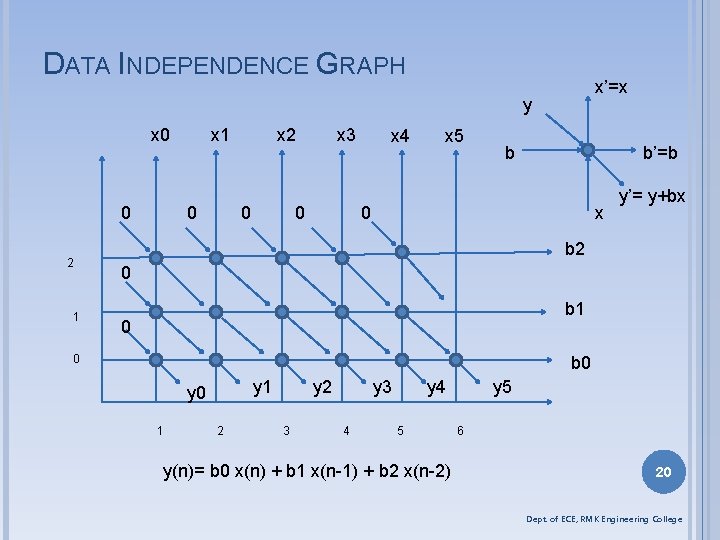
DATA INDEPENDENCE GRAPH x’=x y x 0 0 2 1 x 1 0 x 2 0 x 3 0 x 4 x 5 b b’=b 0 x y’= y+bx b 2 0 b 1 0 0 b 0 y 1 y 0 1 2 y 2 3 y 3 4 y 4 5 y(n)= b 0 x(n) + b 1 x(n-1) + b 2 x(n-2) y 5 6 20 Dept. of ECE, RMK Engineering College

PIPELINING IN FIR FILTERS Reduce the critical path Increase the clock speed or sample speed Reduce power consumption Introduce pipelining latches along the data path 21 Dept. of ECE, RMK Engineering College

PIPELINING IN FIR FILTERS Critical path : TM+2 TA => TM+TA 22 Dept. of ECE, RMK Engineering College

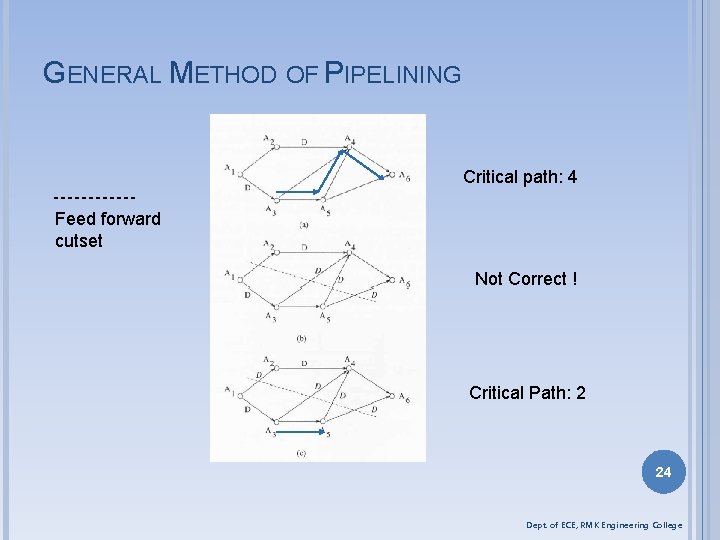
GENERAL METHOD OF PIPELINING Pipelining latches can only be placed across any feed-forward cutset of the graph without affecting of the structure Cutset: A cutset is a set of edges of a graph such that if these edges are removed from the graph, the graph becomes disjoint. Feed-forward cutset: A cutset is called a feedforward cutset if the data move in the forward direction on all the edges of the cutset Limitations of Pipelining Increase in Latency : The difference in the availability of the first output Increase in the number of latches 23 Dept. of ECE, RMK Engineering College

GENERAL METHOD OF PIPELINING Critical path: 4 Feed forward cutset Not Correct ! Critical Path: 2 24 Dept. of ECE, RMK Engineering College

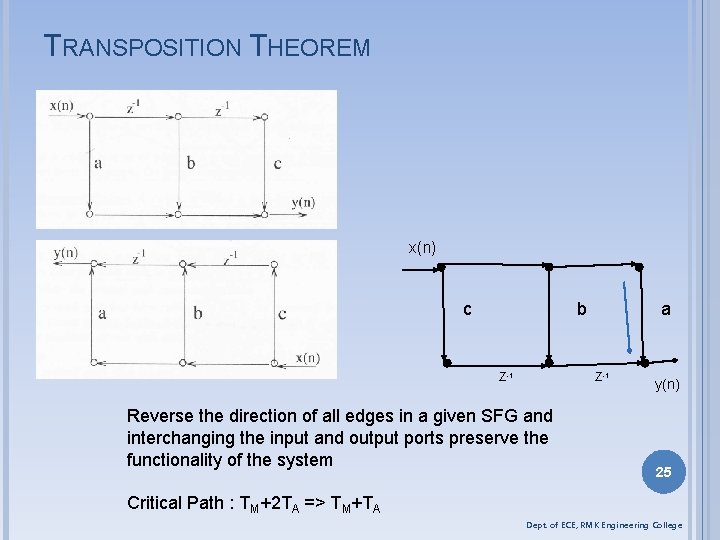
TRANSPOSITION THEOREM x(n) c b Z-1 a Z-1 Reverse the direction of all edges in a given SFG and interchanging the input and output ports preserve the functionality of the system y(n) 25 Critical Path : TM+2 TA => TM+TA Dept. of ECE, RMK Engineering College

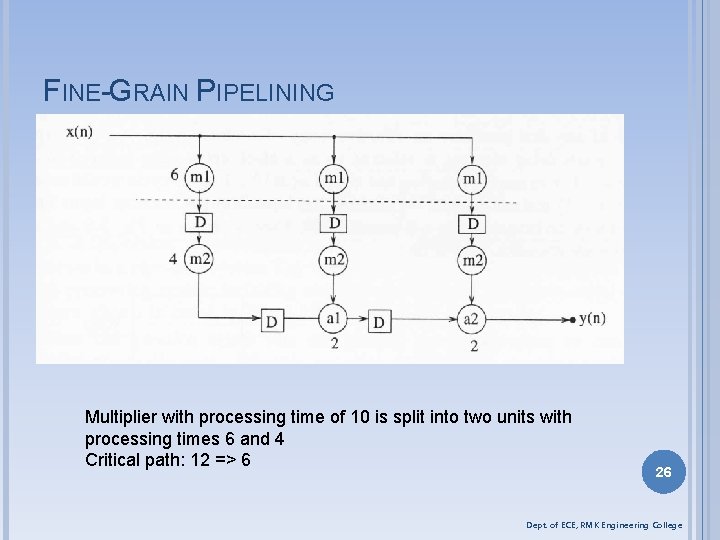
FINE-GRAIN PIPELINING Multiplier with processing time of 10 is split into two units with processing times 6 and 4 Critical path: 12 => 6 26 Dept. of ECE, RMK Engineering College

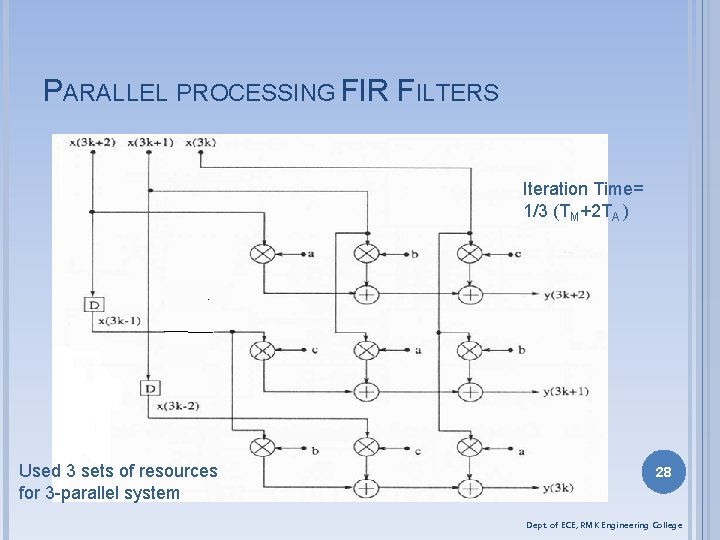
PARALLEL PROCESSING FIR FILTERS y(n)= ax(n)+bx(n-1)+cx(n-2) y(3 k) = ax(3 k)+bx(3 k-1)+cx(3 k-2) y(3 k+1)= ax(3 k+1)+bx(3 k)+cx(3 k-1) y(3 k+2)= ax(3 k+2)+bx(3 k+1)+cx(3 k) Sample speed is increased since multiple samples are processed at the same time. Clock speed remains the same 27 Dept. of ECE, RMK Engineering College

PARALLEL PROCESSING FIR FILTERS Iteration Time= 1/3 (TM+2 TA ) Used 3 sets of resources for 3 -parallel system 28 Dept. of ECE, RMK Engineering College

PIPELINING FOR LOW POWER Ccharge V 0 Propagation delay = -------k(V 0 - Vt)2 Power consumption = Ctotal V 02 f For M Level pipelining Ccharge is reduced by 1/M Keeping f same reduce V 0 by β V 0 where β 0 to 1 Ppip = Ctotal β 2 V 02 f = β 2 Pseq Ccharge/M β V 0 Propagation delaypip = ----------k(βV 0 - Vt)2 If the clock period is kept the same Ccharge V 0 ------k(V 0 - Vt)2 (βV 0 - Vt)2 = = Ccharge/M β V 0 ---------k(βV 0 - Vt)2 β (V 0 - Vt)2 29 Solve for β Dept. of ECE, RMK Engineering College

EXAMPLE ON PIPELINING Consider an original 3 -tap FIR filter and its finegrain pipeline. Assume TM=10 ut, TA=2 ut, Vt=0. 6 V, Vo=5 V, and CM=5 CA. In fine-grain pipeline filter, the multiplier is broken into 2 parts, m 1 and m 2 with computation time of 6 u. t. and 4 u. t. respectively, with capacitance 3 times and 2 times that of an adder, respectively. (a) What is the supply voltage of the pipelined filter if the clock period remains unchanged? (b) What is the power consumption of the pipelined filter as a percentage of the original filter? 30 Dept. of ECE, RMK Engineering College

SOLUTION Solution: Original : C charge = CM + CA = 6 CA Pipelining : C charge = 3 C A (5 β - 0. 6)2 = β (5 - 0. 6)2 β = 0. 6033 or 0. 0239 ( not valid) Vpip = 3. 0165 V 0 Ppip = 0. 364 Pseq 31 Dept. of ECE, RMK Engineering College

PARALLEL SYSTEM FOR LOW POWER Power consumption : Ppar = (L Ctotal) (β V 0)2 f / L = P seq for L- Parallel System Propagation delay: Ccharge V 0 Tseq = -------k(V 0 - Vt)2 L Tseq = Tpar = Ccharge β V 0 --------k(βV 0 - Vt)2 β(V 0 - Vt)2 = L (βV 0 - Vt)2 Solve for β 32 Dept. of ECE, RMK Engineering College

EXAMPLE ON PARALLEL SYSTEM Consider a 4 -tap FIR filter shown in Fig. 3. 18(a) and its 2 -parallel version in 3. 18(b). The two architectures are operated at the sample period 9 u. t. Assume TM=8, TA=1, Vt=0. 45 V, Vo=3. 3 V, CM=8 CA (a) What is the supply voltage of the 2 -parallel filter? (b) What is the power consumption of the 2 parallel filter as a percentage of the original filter? 33 Dept. of ECE, RMK Engineering College

SOLUTION Ccharge = CM + CA 2 - parallel: Ccharge = CM + 2 CA = 10 CA 9 (β 3. 3 - 0. 45)2 = 5 β (3. 3 - 0. 45)2 β = 0. 6585 or 0. 0282 (not valid) Vpar = 2. 1743 Vo Ppar = 0. 4341 P 34 Dept. of ECE, RMK Engineering College

PROBLEMS & ASSIGNMENTS 1) Prob. 2. 7. 1 (a) 2) Prob. 2. 7. 4 Assignment 1) Design a Low pass filter with sample rate of 48 KHz and order 40 with cut off frequency of 10 KHz. Write VHDL/Verilog code and simulate Hint: Use Matlab to find the coefficients and test the filter functionality by testing the impulse response 2) Implement a 4 -tap filter in direct form and in transpose form. Introduce pipelining and compare the performance 35 Dept. of ECE, RMK Engineering College