VLSI Physical Design Automation Lecture 5 Circuit Partitioning

VLSI Physical Design Automation Lecture 5. Circuit Partitioning (III) Spectral and Flow Prof. David Pan dpan@ece. utexas. edu Office: ACES 5. 434 11/27/2020 1

Recap of what you have learned a KL Algorithm a FM algorithm a Variation and Extension a Multilevel partition (h. Metis) a Simulated Annealing 11/27/2020 2

Partitioning Algorithms a. Two elegant partition algorithms a although not the fastest a. Learn how to formulate the problem! a=> Key to VLSI CAD (1) Spectral based partitioning algorithms (2) Max-flow based partition algorithm 11/27/2020 3

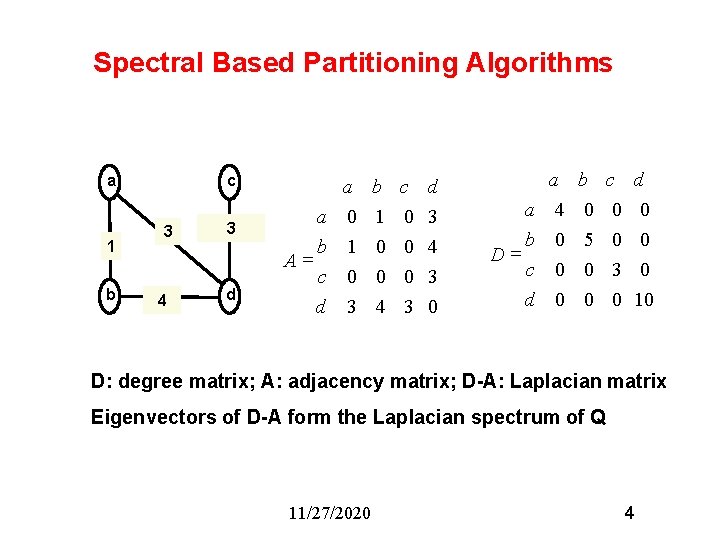
Spectral Based Partitioning Algorithms a 1 b c 3 4 3 d a b A= c d a 0 1 0 3 b 1 0 0 4 c 0 0 0 3 d 3 4 3 0 a b = D c d a 4 0 0 0 b 0 5 0 0 c 0 0 3 0 d 0 0 0 10 D: degree matrix; A: adjacency matrix; D-A: Laplacian matrix Eigenvectors of D-A form the Laplacian spectrum of Q 11/27/2020 4

Eigenvalues and Eigenvectors x A æ a 11 a 12 çç. . . è an 1 an 2 If Ax æ x 1 ö æ a 11 x 1 + a 12 x 2 + L + a 1 n xn L a 1 n öç ÷ ç ÷÷ç M ÷ = ç M L ann øçè xn ÷ø çè an 1 x 1 + an 2 x 2 + L + ann xn ö ÷ ÷ ÷ ø Ax= x then is an eigenvalue of A x is an eignevector of A w. r. t. (note that Kx is also a eigenvector, for any constant K). 11/27/2020 5

A Basic Property x. TAx æ a 11 ç = (x 1 , L , xn )ç ça è n 1 æn = ç åxi ai 1, è i =1 = åx x a i L L a 1 n öæ x 1 ö ÷ç ÷ ÷ç M ÷ç x ÷ a L nn øè n ø æ x 1 ö n öç ÷ xi ain, ÷ç M ÷ å øç ÷ i =1 è xn ø j ij i, j 11/27/2020 6

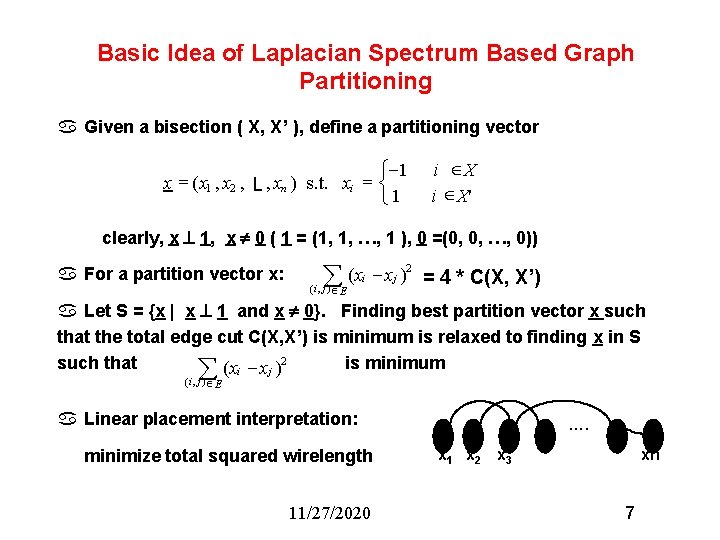
Basic Idea of Laplacian Spectrum Based Graph Partitioning a Given a bisection ( X, X’ ), define a partitioning vector ì-1 = = x ( x 1 , x 2 , L , xn ) s. t. xi í î 1 i ÎX i Î X' clearly, x 1, x 0 ( 1 = (1, 1, …, 1 ), 0 =(0, 0, …, 0)) a For a partition vector x: å (x ( i , j )Î E i - xj )2 = 4 * C(X, X’) a Let S = {x | x 1 and x 0}. Finding best partition vector x such that the total edge cut C(X, X’) is minimum is relaxed to finding x in S such that is minimum å ( xi - xj )2 ( i , j )Î E a Linear placement interpretation: minimize total squared wirelength 11/27/2020 …. x 1 x 2 x 3 xn 7

Property of Laplacian Matrix (1) x. T Qx = åQ x x ij i j = x. T Dx - x. T Ax åd x = = 2 i i - åAij xi xj 2 i i - å( x ( i , j ) ÎE i å 2 aijx x ( i , j ) ÎE - xj )2 = 4 * C(X, X’) i …. j x 1 x 2 x 3 xn squared wirelength If x is a partition vector Therefore, we want to minimize x. T Qx 11/27/2020 8

Property of Laplacian Matrix (Cont’d) ( 2 ) Q is symmetric and semi-definite, i. e. T (i) x Qx = åQ x x ij i j 0 (ii) all eigenvalues of Q are 0 ( 3 ) The smallest eigenvalue of Q is 0 corresponding eigenvector of Q is x 0= (1, 1, …, 1 ) (not interesting, all modules overlap and x 0 S ) ( 4 ) According to Courant-Fischer minimax principle: the 2 nd smallest eigenvalue satisfies: x. T Qx l = min x in S | x |2 11/27/2020 9

Results on Spectral Based Graph Partitioning a Min bisection cost c(x, x’) n /4 a Min ratio-cut cost c(x, x’)/|x| |x’| /n a The second smallest eigenvalue gives the best linear placement a Compute the best bisection or ratio-cut based on the second smallest eigenvector 11/27/2020 10

Computing the Eigenvector a. Only need one eigenvector (the second smallest one) a. Q is symmetric and sparse a. Use block Lanczos Algorithm 11/27/2020 11

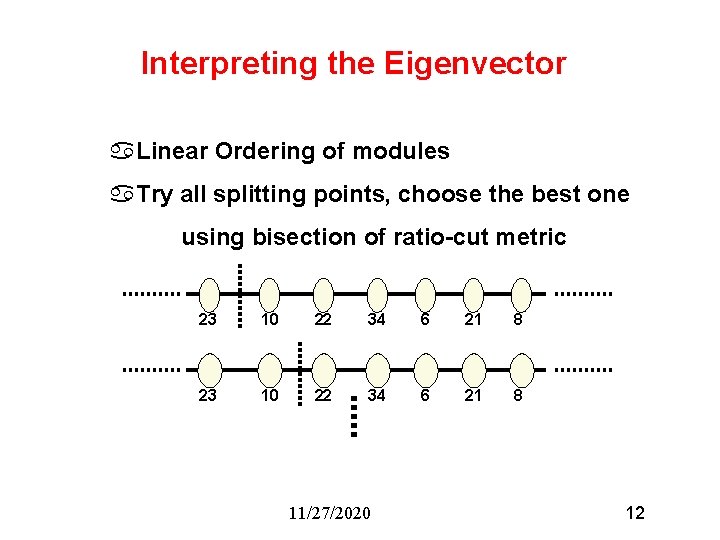
Interpreting the Eigenvector a. Linear Ordering of modules a. Try all splitting points, choose the best one using bisection of ratio-cut metric 23 10 22 34 6 21 8 11/27/2020 12

Experiments on Special Graphs a. GBUI(2 n, d, b) [Bui-Chaudhurl-Leighton 1987] n n 2 n nodes d-regular min-bisection b GBUI Results Cluster 2 Value of Xi Module i Cluster 1 11/27/2020 13

Some Applications of Laplacian Spectrum a. Placement and floorplan [Hall 1970] [Otten 1982] [Frankle-Karp 1986] [Tsay-Kuh 1986] a. Bisection lower bound and computation [Donath-Hoffman 1973] [Barnes 1982] [Boppana 1987] a. Ratio-cut lower bound and computation [Hagen-Kahng 1991] [Cong-Hagen-Kahng 1992] 11/27/2020 14