VLSI CAD Flow Logic Synthesis Placement and Routing

VLSI CAD Flow: Logic Synthesis, Placement and Routing 6. 375 Lecture 5 Guest Lecture by Srini Devadas 1

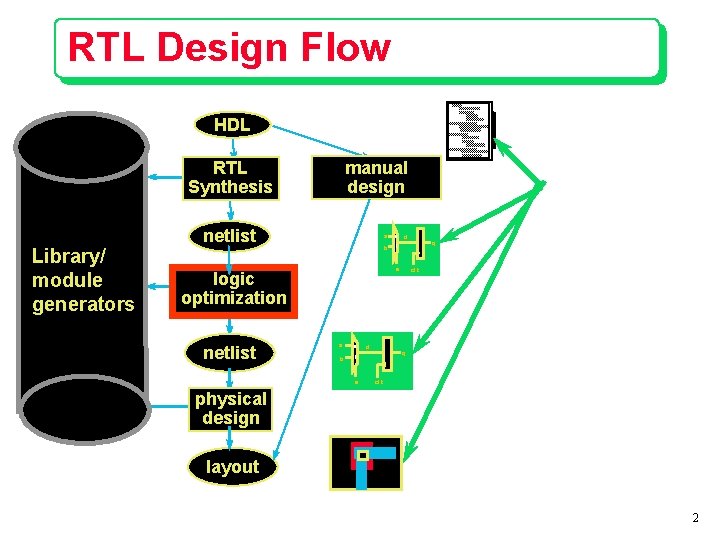
RTL Design Flow HDL manual design RTL Synthesis Library/ module generators netlist 0 b 1 d s logic optimization netlist a a 0 b 1 s d q clk physical design layout 2

Two-Level Logic Minimization Can realize an arbitrary logic function in sum-of-products or two-level form F 1 = A B + A B D + A B C D +ABCD+AB+ABD F 1 = B + D + A C Of great interest to find a minimum sum-ofproducts representation – Solved problem even for functions with 100’s of inputs (variants of Quine-Mc. Cluskey) 3

Two-Level versus Multilevel 2 -Level: f 1 = AB + AC + AD f 2 = AB + AC + AE 6 product terms which cannot be shared. 24 transistors in static CMOS Multi-level: Note that B + C is a common term in f 1 and f 2 K=B+C f 1 = AK + AD f 2 = AK + AE 3 Levels 20 transistors in static CMOS not counting inverters 4

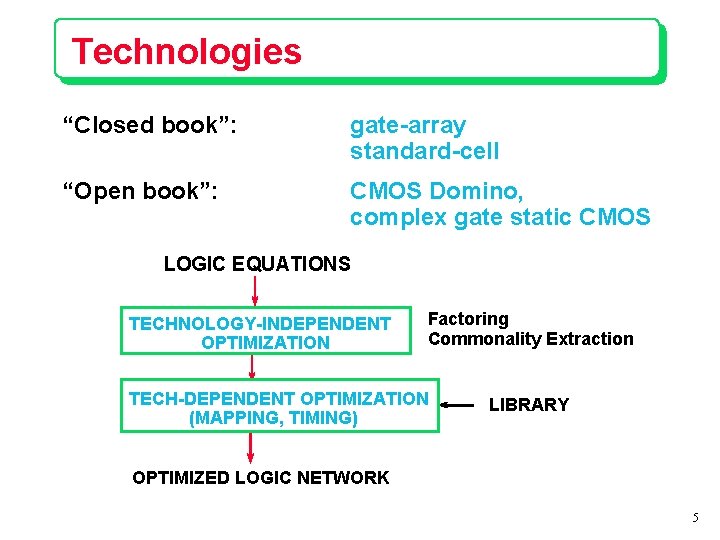
Technologies “Closed book”: gate-array standard-cell “Open book”: CMOS Domino, complex gate static CMOS LOGIC EQUATIONS TECHNOLOGY-INDEPENDENT OPTIMIZATION Factoring Commonality Extraction TECH-DEPENDENT OPTIMIZATION (MAPPING, TIMING) LIBRARY OPTIMIZED LOGIC NETWORK 5

Tech. -Independent Optimization Involves: Minimizing two-level logic functions. Finding common subexpressions. Substituting one expression into another. Factoring single functions. Factored versus Disjunctive forms f = ac + ad + bc + bd + a e sum-of-products or disjunctive form f = ( a + b )( c + d ) + a e factored form multi-level or complex gate 6

Optimizations f 1 = AB + AC + AD + AE + A BC D E ì F=í î f 2 = AB + AC + AD + AF + A BC D F Factor F ì f 1 = A( B + C + D + E) + ABC DE F=í î f 2 = A( B + C + D + F) + ABC DF Extract common expression ì g 1 = B + C + D G = í f 1 = A ( g 1 + E ) + A E g 1 ï î f 2 = A ( g 1 + F ) + A F g 1 7

What Does “Best” Mean? Transistor count AREA Number of circuits POWER Number of levels DELAY (Speed) Need quick estimators of area, delay and power which are also accurate 8

Algebraic vs. Boolean Methods Algebraic techniques view equations as polynomials and attempt to factor equations or “divide” them Do not exploit Boolean identities e. g. , a a = 0 In algebraic substitution (or division) if a function f = f(a, b, c) is divided by g = g(a, b), a and b will not appear in f / g Algebraic division: O(n log n) time Boolean division: 2 -level minimization required 9

Comparison f = ab + ac + b a + bc + ca + cb Algebraic factorization procedures f = a(b + c ) + a (b + c ) + b c + c b Boolean factorization produces f = ( a + b + c ) l = ( b f + b f ) ( a + e ) + ae ( b f + bf ) r = ( b f + b f ) ( a + e ) + ae ( b f + bf ) Algebraic substitution of l into r fails Boolean substitution r = a ( e l + e l ) + a ( el + e l ) l = a ( er + e r ) + a ( er + e r ) 10

Strong (or Boolean) Division Given a function f to be strong divided by g Add an extra input to f corresponding to g, namely G and obtain function h as follows h. DC = G g + Gg h. ON = f. ON - h. DC Minimize h using two-level minimizer 11

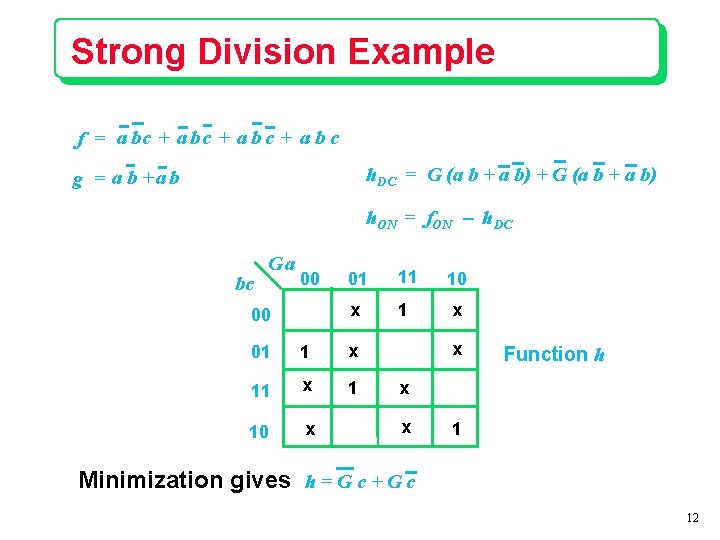
Strong Division Example f = a bc + a b c h. DC = G (a b + a b) + G (a b + a b) g = a b +a b h. ON = f. ON - h. DC bc Ga 00 00 01 11 10 x 1 x 01 1 x 1 10 x x Function h x x 1 Minimization gives h = G c + G c 12

Weak (or Algebraic) Division Definition: support of f as sup( f ) = { set of all variables v that occur in f as v or v } Example: f=AB+C sup( f ) = { A, B, C } Definition: we say that f is orthogonal to g, f ^ g, if sup( f ) Ç sup( g ) = f Example: f=A+B g=C+D f ^ g since { A, B } Ç { C, D } = f 13

Weak Division - 2 We say that g divides f weakly if there exist h, r such that f = gh + r where h ¹ f and g ^ h Example: f = ab + ac + d g=b+c f = a(b + c) + d h=a r=d We say that g divides f evenly if r = f The quotient f / g is the largest h such that f = gh + r i. e. , f = ( f / g )g + r 14

Weak Division Example f = abc + abde + abh + bcd g = c + de + h Theorem: f / g = f / c Ç f / de Ç f / h f / c = ab + bd f / de = ab f / h = ab f / g = (ab + bd) Ç ab = ab f = ab(c + de + h) + bcd Time complexity: O( | f | | g | ) 15

How to Find Good Divisors? $64 K question Strong division: Use existing nodes in the multilevel network to simplify other nodes Weak division: Generate good algebraic divisors using algorithms based on “kernels” of an algebraic expression 16

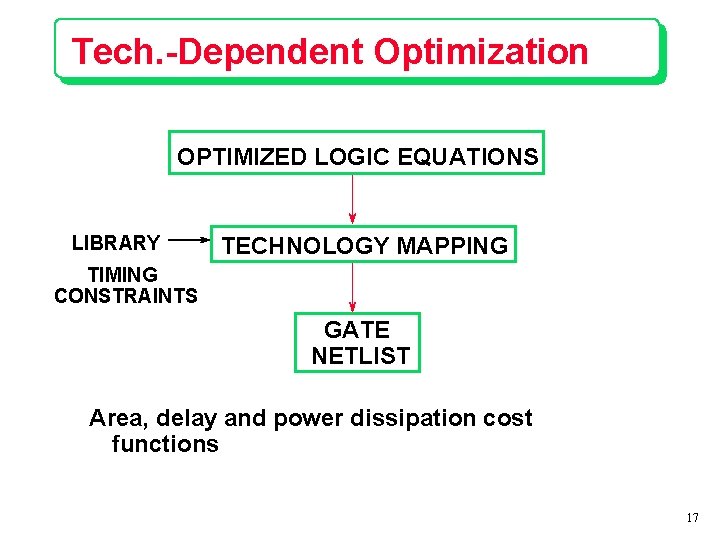
Tech. -Dependent Optimization OPTIMIZED LOGIC EQUATIONS LIBRARY TECHNOLOGY MAPPING TIMING CONSTRAINTS GATE NETLIST Area, delay and power dissipation cost functions 17

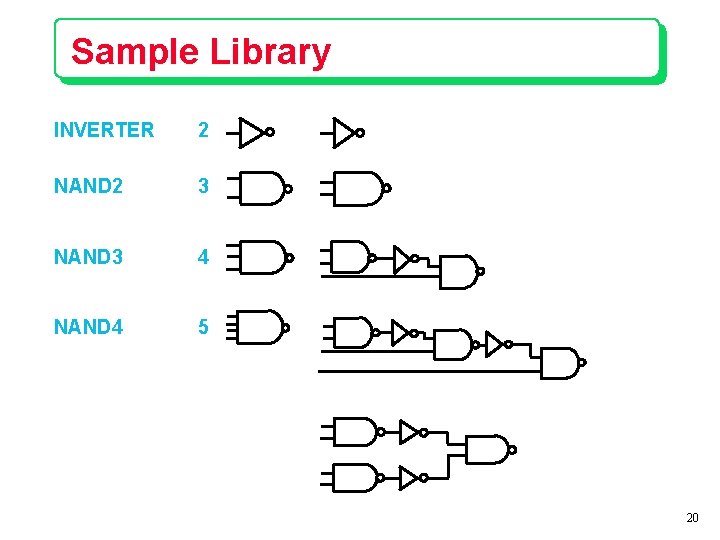
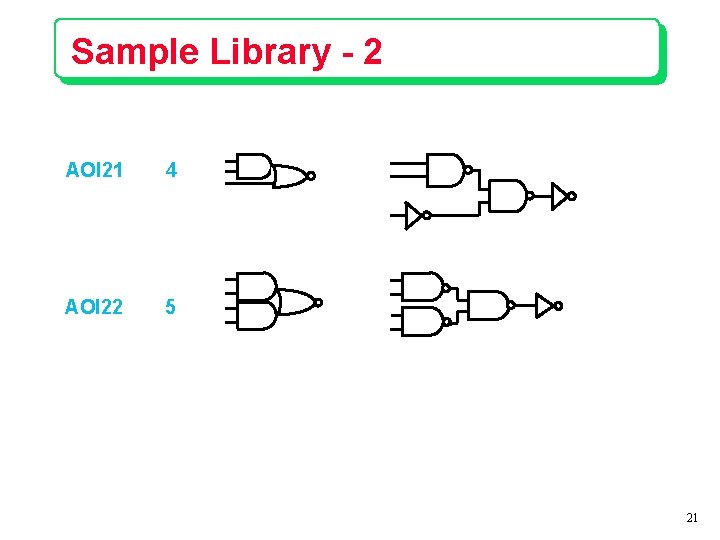
“Closed Book” Technologies A standard cell technology or library is typically restricted to a few tens of gates e. g. , MSU library: 31 cells Gates may be NAND, NOR, NOT, AOIs. B A A C AB+C B 18

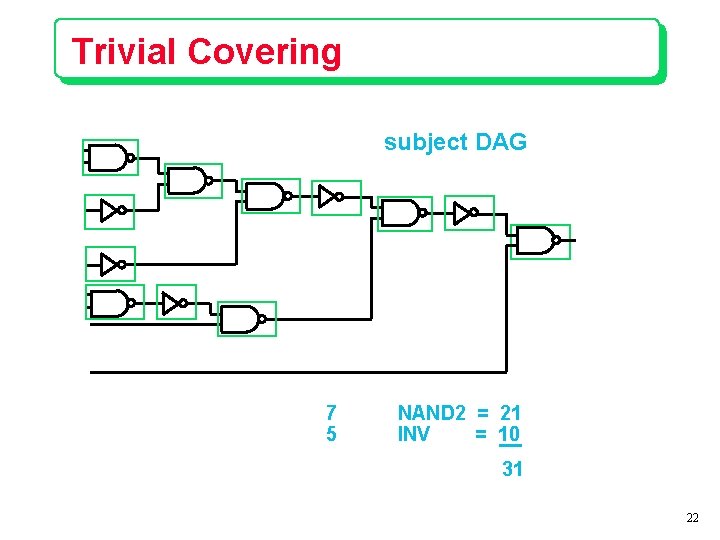
Mapping via DAG Covering Represent network in canonical form Þ subject DAG Represent each library gate with canonical forms for the logic function Þ primitive DAGs Each primitive DAG has a cost Goal: Find a minimum cost covering of the subject DAG by the primitive DAGs Canonical form: 2 -input NAND gates and inverters 19

Sample Library INVERTER 2 NAND 2 3 NAND 3 4 NAND 4 5 20

Sample Library - 2 AOI 21 4 AOI 22 5 21

Trivial Covering subject DAG 7 5 NAND 2 = 21 INV = 10 31 22

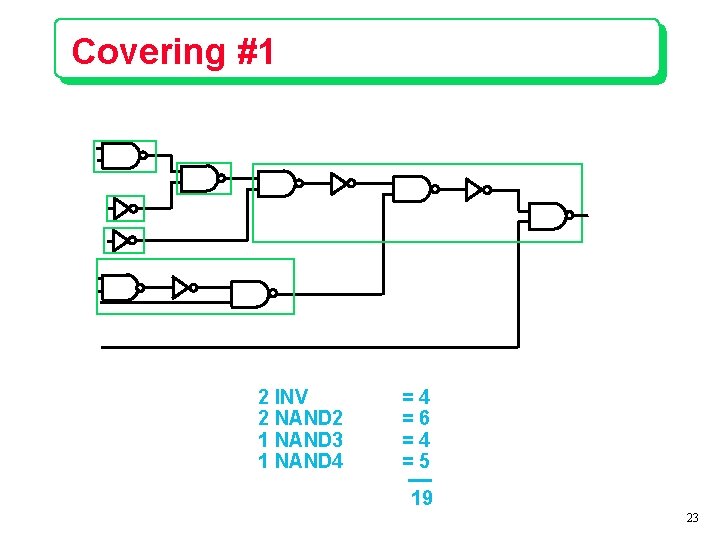
Covering #1 2 INV 2 NAND 2 1 NAND 3 1 NAND 4 =4 =6 =4 =5 19 23

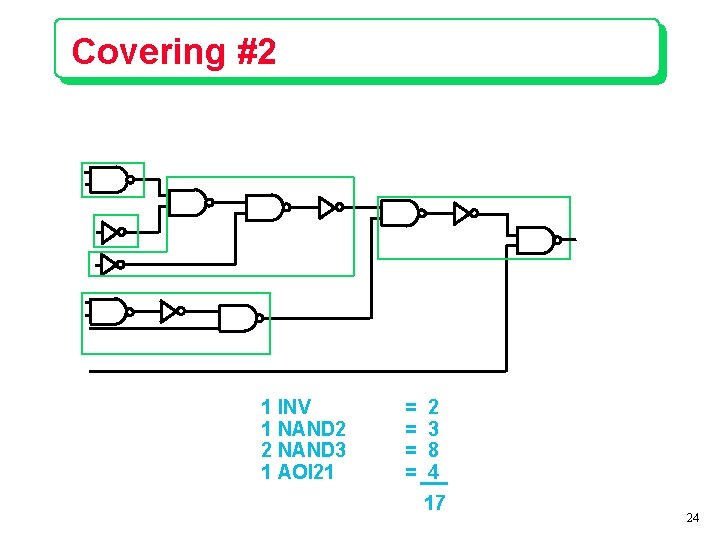
Covering #2 1 INV 1 NAND 2 2 NAND 3 1 AOI 21 = = 2 3 8 4 17 24

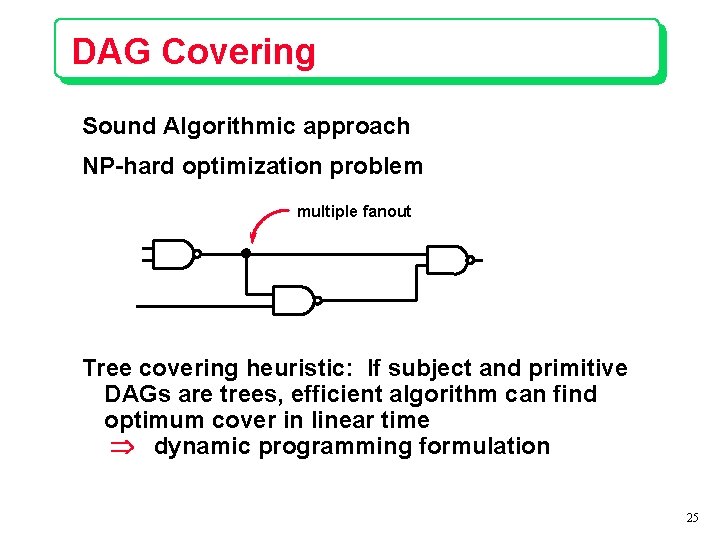
DAG Covering Sound Algorithmic approach NP-hard optimization problem multiple fanout Tree covering heuristic: If subject and primitive DAGs are trees, efficient algorithm can find optimum cover in linear time Þ dynamic programming formulation 25

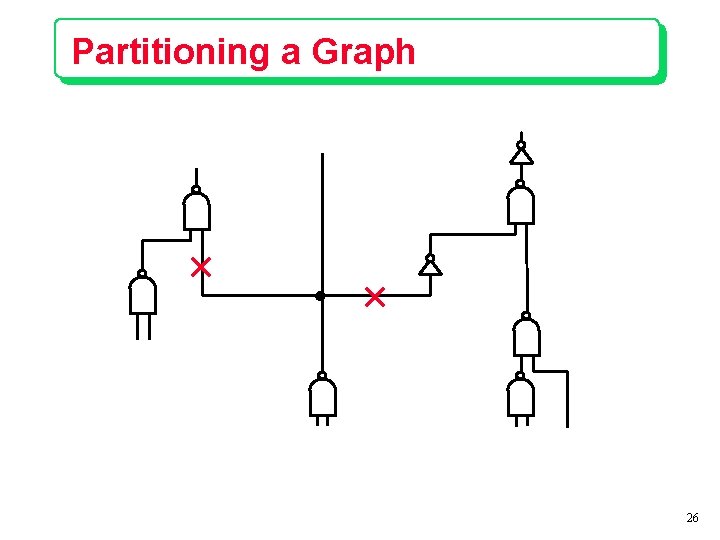
Partitioning a Graph 26

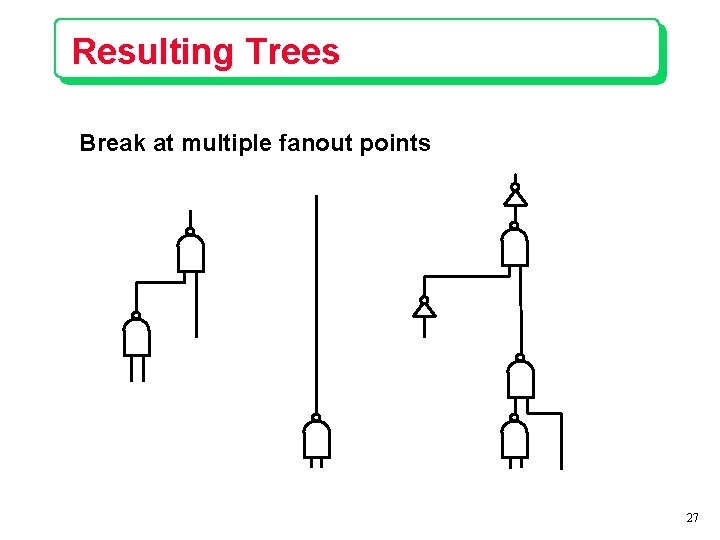
Resulting Trees Break at multiple fanout points 27

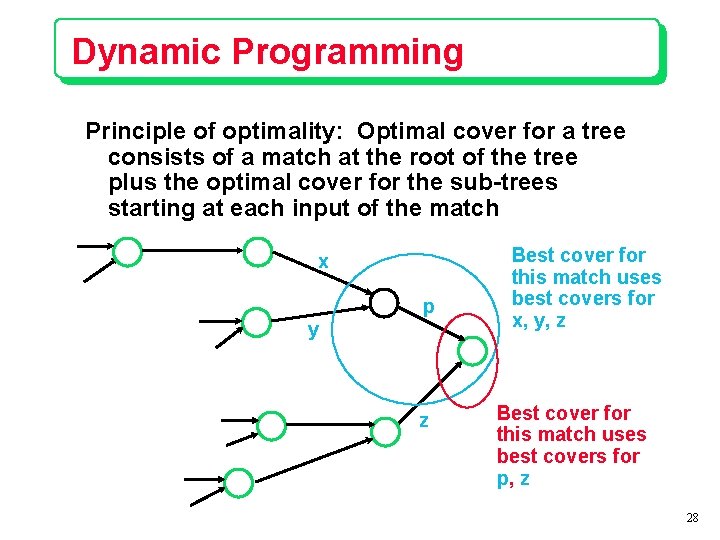
Dynamic Programming Principle of optimality: Optimal cover for a tree consists of a match at the root of the tree plus the optimal cover for the sub-trees starting at each input of the match x p y z Best cover for this match uses best covers for x, y, z Best cover for this match uses best covers for p, z 28

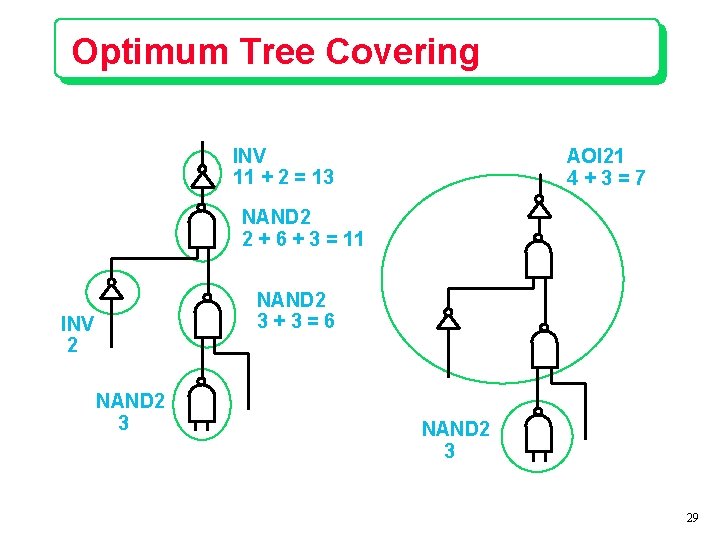
Optimum Tree Covering INV 11 + 2 = 13 AOI 21 4+3=7 NAND 2 2 + 6 + 3 = 11 NAND 2 3+3=6 INV 2 NAND 2 3 29