VLSI Arithmetic Multiplication A an1 an2 a 1

VLSI Arithmetic

Multiplication A = an-1 an-2 … a 1 a 0 B = bn-1 bn-2 … b 1 b 0 Shift and add Area O(N) Time O(Nlog. N) Too slow eg) 110011 101001 110011 000000 110011

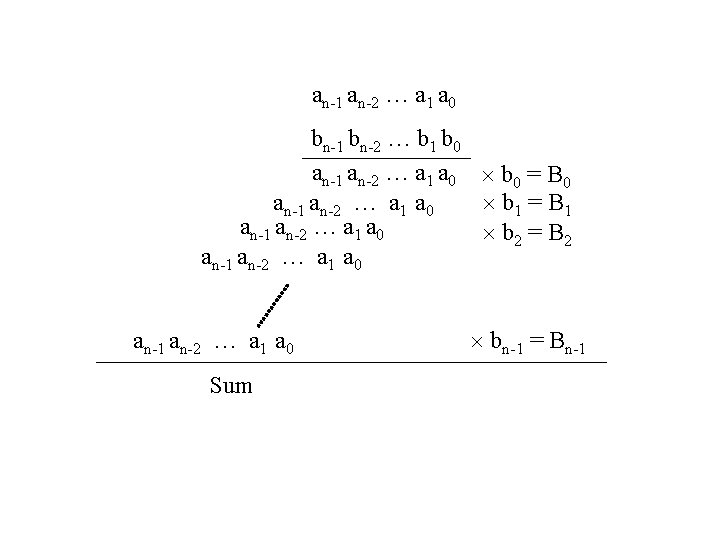
an-1 an-2 … a 1 a 0 bn-1 bn-2 … b 1 b 0 an-1 an-2 … a 1 a 0 b 0 = B 0 an-1 an-2 … a 1 a 0 b 1 = B 1 an-2 … a 1 a 0 b 2 = B 2 an-1 an-2 … a 1 a 0 Sum bn-1 = Bn-1

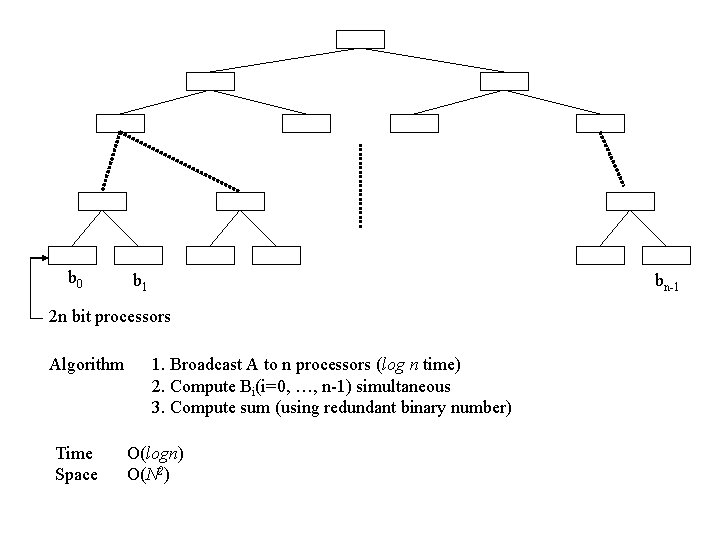
b 0 b 1 bn-1 2 n bit processors Algorithm Time Space 1. Broadcast A to n processors (log n time) 2. Compute Bi(i=0, …, n-1) simultaneous 3. Compute sum (using redundant binary number) O(logn) O(N 2)

3 M - multiplication (Why not 4 M - multiplication? ) P=X • Y U = (X 1+X 0) (Y 1+Y 0) V = (X 1 • Y 1) W = (X 0 • Y 0) P = (X • Y) = V • 2 N + (U-V-W) • 2 N/2 + W A = O(N 2) T = O(log N) X Y Input distribution (X 1+ X 0) (Y 1+ Y 0) Routing X 1 • Y 1 (X 1+ X 0) (Y 1+ Y 0) X 0 • Y 0 Routing Adder (n) Output network recursively

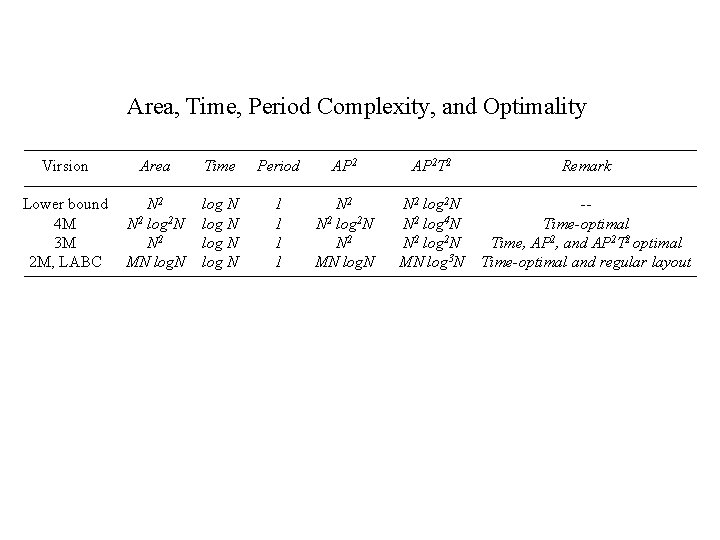
Area, Time, Period Complexity, and Optimality Virsion Area Time Period AP 2 T 2 Remark Lower bound 4 M 3 M 2 M, LABC N 2 log 2 N N 2 MN log N 1 1 N 2 log 2 N N 2 MN log. N N 2 log 2 N N 2 log 4 N N 2 log 2 N MN log 3 N -Time-optimal Time, AP 2, and AP 2 T 2 optimal Time-optimal and regular layout

Redundant Binary Number (Signed Digit) where ai {0, 1, 1} Example. 1 1 0 1 1 1 = 2 5 - 24 + 2 2 + 2 1 - 20 1. Binary number is a redundant binary number 2. Note that 1 = 1 1 3. Redundant binary number Binary Number by subtraction (in log n time)

Example 1 1 1 0 1 = 10100 - 1001 = 15 Example addition 111101 + 100110 S=011011 110010 1111111 (5)10 (38)10 (sum)

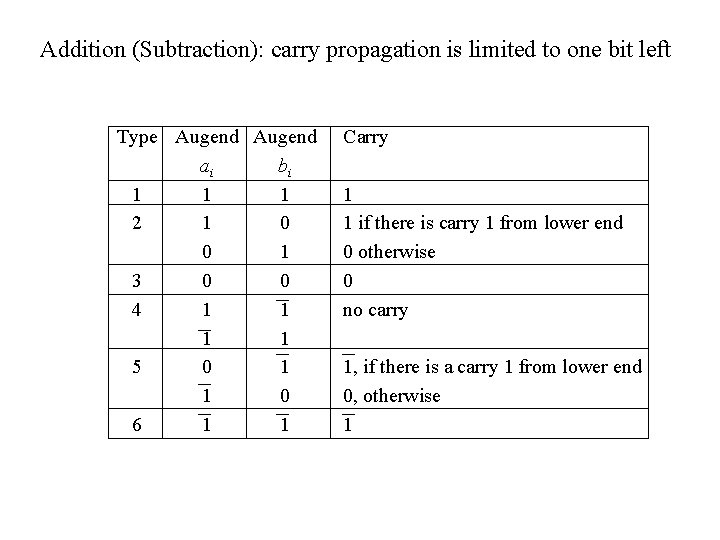
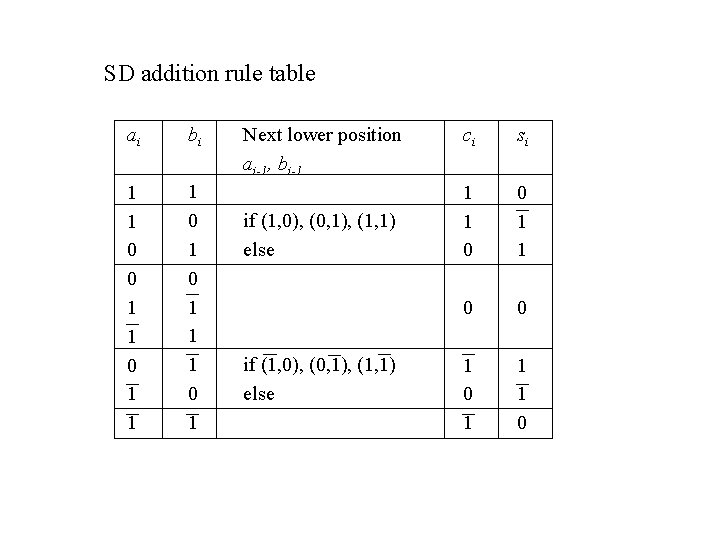
Addition (Subtraction): carry propagation is limited to one bit left Type Augend ai bi 1 1 1 2 1 0 0 1 3 0 0 4 1 1 5 0 1 1 0 6 1 1 Carry 1 1 if there is carry 1 from lower end 0 otherwise 0 no carry 1, if there is a carry 1 from lower end 0, otherwise 1

SD addition rule table ai bi 1 1 0 0 1 1 1 0 1 Next lower position ai-1, bi-1 if (1, 0), (0, 1), (1, 1) else ci si 1 1 0 0 1 0 1 1 1 0

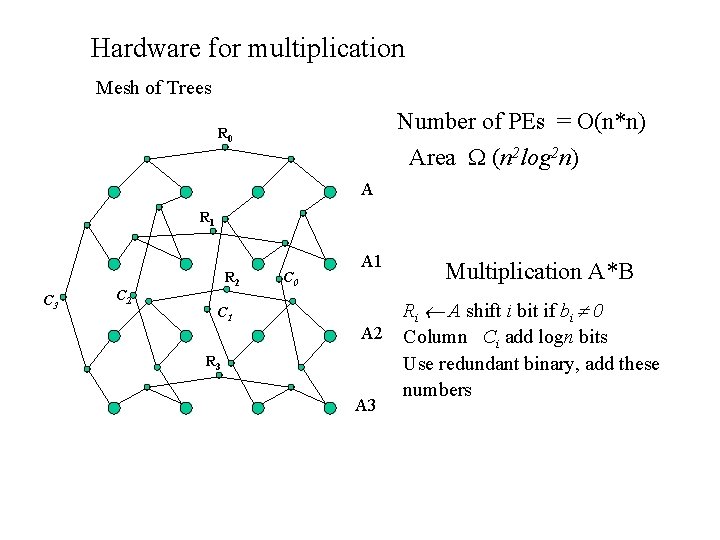
Hardware for multiplication Mesh of Trees Number of PEs = O(n*n) R 0 Area (n 2 log 2 n) A R 1 C 3 C 2 R 2 C 0 A 1 C 1 A 2 R 3 A 3 Multiplication A*B Ri A shift i bit if bi 0 Column Ci add logn bits Use redundant binary, add these numbers

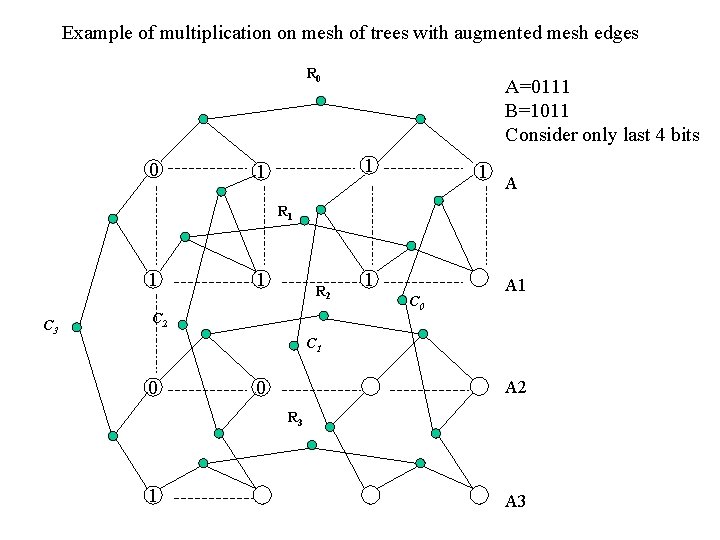
Example of multiplication on mesh of trees with augmented mesh edges R 0 0 A=0111 B=1011 Consider only last 4 bits 1 1 1 A R 1 1 C 3 1 R 2 C 2 1 C 0 A 1 C 1 0 0 A 2 R 3 1 A 3

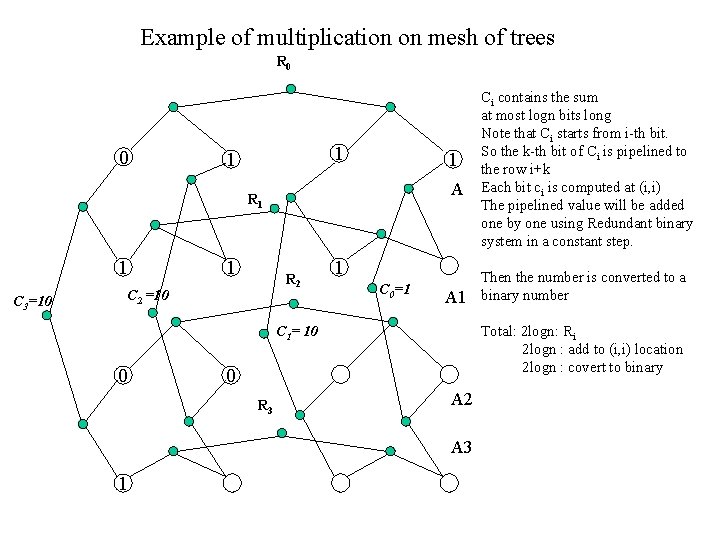
Example of multiplication on mesh of trees R 0 0 1 1 1 A R 1 1 C 3=10 1 R 2 C 2 =10 1 C 0=1 A 1 C 1= 10 0 A 2 A 3 1 Then the number is converted to a binary number Total: 2 logn: Ri 2 logn : add to (i, i) location 2 logn : covert to binary 0 R 3 Ci contains the sum at most logn bits long Note that Ci starts from i-th bit. So the k-th bit of Ci is pipelined to the row i+k Each bit ci is computed at (i, i) The pipelined value will be added one by one using Redundant binary system in a constant step.

Integer Division • Not as easy • O(logn) algorithm exist with table look up • Hardware circuit exist? => open question

Newton Rapson Method To solve f(x) = 0, To find , let Newton Rapson Method converges quadratically, That is, i+1 = i 2

Eg. When D = 4 set x 0 = 0. 4 x 1 = 0. 16 x 2 = 0. 2176 x 3 = 0. 245801 0 = 0. 15 1 = 0. 09 2 = 0. 0324 3 = 0. 004199 To get n precision reciprocal of D, we need logn iterations. 1 st iteration: 1 digit correct 2 nd iteration: 2 didit correct 3 rd iteration: 4 digit correct logn iterations: n digit correct

Proof that Newton Rapson Method converges quadratically. Let X be the solution of f(x) = 0. But where Since f(X) = 0, we have Thus, Since f”( ) is bounded and f’(xi) is bounded, | i+1 | = c | i |2, for some c For is bounded if D 0

Complexity • Each *: O(logn) time • to obtain n digit precision, O(logn) iteration • => O(log 2 n) complexity • A/D => A * (1/D) • Question: logn algorithm for division?