Viterbi Detector Review of Fast Algorithm and Implementation

Viterbi Detector: Review of Fast Algorithm and Implementation -Xiaohong Sheng ECE 734 Project

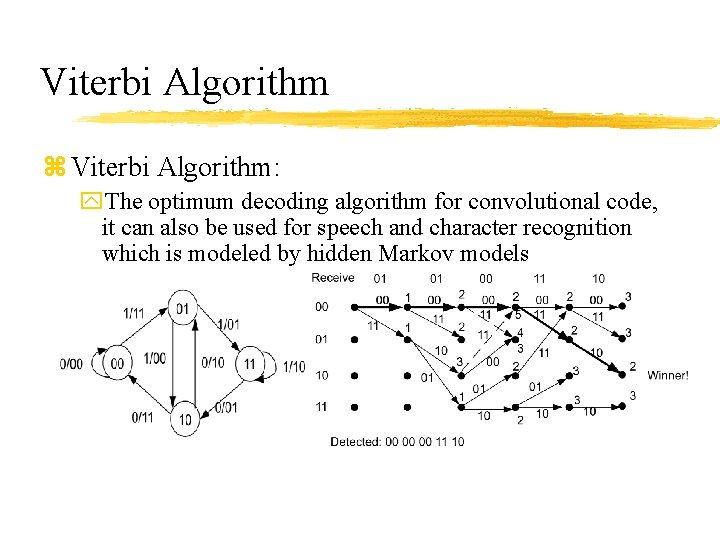
Viterbi Algorithm z Viterbi Algorithm: y. The optimum decoding algorithm for convolutional code, it can also be used for speech and character recognition which is modeled by hidden Markov models

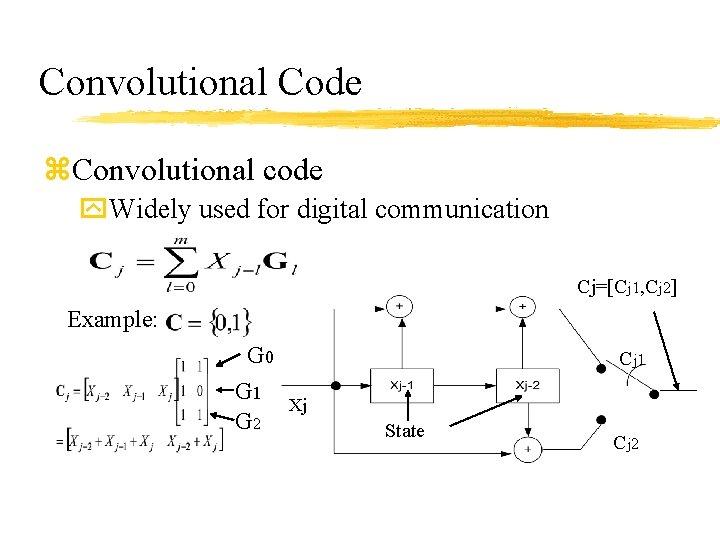
Convolutional Code z. Convolutional code y. Widely used for digital communication Cj=[Cj 1, Cj 2] Example: G 0 G 1 G 2 Cj 1 Xj State Cj 2

Problems on Viterbi Algorithm z Computational complexity increases exponentially with constraint length (state) of convolutional code z Nonlinear feedback loop in the VA presents a bottleneck for High speed implementations z Other issues such as: y. Viterbi algorithm is a ML (optimum) algorithm if Euclidean distance is used. The usually used Hamming distance in VA is sub-optimum and therefore lose some performance. y If Euclidean distance is used, The use of multiplier increases the decoder complexity significantly

Any Solution? z YES! z Two main solutions y. Reduce state • At least half of the states can be reduced for DPSK sources. – Exciting! -Yes, Believe? -? , How? And any other problem can be induced? y. Pipeline x. Solve the bottleneck of nonlinear feedback? z Others solutions like y. Linear distance metric can be used y. Select some special convolutional codes

Reduced state solution z. DPSK sources Received signal at the ith receiver for QAM data communication system can be described as When Xi(t) is oversampled by K, hi(t) lasts a maximum of d symbol intervals and put all data from N receivers in a vector, the signals can be modeled as: Under the assumptions on: a)Si are orthonormal, b) Noise is Gaussian Use SVD Use Mahalanobis orthogonalization transform

Reduced state solution (Cont. ) z It can be proven that So, Where: Is affected by input data symbols [St, St-1…St-k-d+1] So, the optimal detection can be defined by: It can be achieved by VA to a M^(d+k-1) states, the original Rx optimal detection achieved by VA has M^(d+k) states. Half of States is reduced

Pipeline Solution z Pipeline y M-Step Trellis (Look Ahead) or y M-Step Trellis+1 -Step Trellis y. Backward and forward Trellis

Other solutions z. Use Linear Distances (For QPSK 8 -PSK, 16 QAM) y. Avoid multiplication without losing the VA decoder performance z. Use doubly complementary convolutional codes y. Save 1/3 of real time operations over the VA with a state grouping and partitioning of the trellis

Other issues I’m thinking. . . z Can we increase the decoder speed infinitely if we have infinite hardware? If not, what’s maximum speed we can achieve? z Is there optimal partitions given the size of the source need to be decoded so that we can achieve maximum decoding speed and use minimum hardware z Woo…, Really hard mathematical problem. And Perhaps no solution z. Interested these problems also?

Reference(1) z [1]. Implementing the Viterbi algorithm, Lou, H. -L. IEEE Signal Processing Magazine , Volume: 12 Issue: 5 , Sept. 1995, Page(s): 42 -52 z [2]. A reduced-state Viterbi algorithm for blind sequence estimation of DPSK sources, Tongtong Li; Zhi Ding Global Telecommunications Conference, 1999. GLOBECOM '99 , Volume: 4 , 1999 , Page(s): 2167 -2171 vol. z [3]. A reduced state Viterbi algorithm for multiuser detection in DS/CDMA systems , Wang Zhaocheng; Ge Ning; Yao Yan; Qiang Wang Communication Technology Proceedings, 1996. ICCT'96. , 1996 International Conference on , Volume: 2 , 1996 Page(s): 1102 -1105 vol. 2 z [4]. Linear distances as branch metrics for viterbi decoding of trellis codes, Hut-Ling Lou Acoustics, Speech, and Signal Processing, 2000. ICASSP '00. Proceedings. 2000 IEEE International Conference on , Volume: 6 , Page(s): 3267 -3270 z [5]. A constraint-length based modified Viterbi algorithm with adaptive effort Feldmann, C. ; Harris, J. H. Communications, IEEE Transactions on, Volume: 47 Issue: 11 , Nov. 1999 Page(s): 1611 – 1614

Reference(2) z [6]. Complexity reduction of the Viterbi algorithm using doubly complementary convolutional codes, Haccoun, D. ; Caron, M. ; Nabli, M. Communications, Computers and Signal Processing, 1999 IEEE Pacific Rim Conference on , 1999 Page(s): 408 – 411 z [7]. High-performance VLSI architecture for the Viterbi algorithm, Boo, M. ; Arguello, F. ; Bruguera, J. D. ; Doallo, R. ; Zapata, E. L. Communications, IEEE Transactions on , Volume: 45 Issue: 2 , Feb. 1997 Page(s): 168 -176 z [8]. Pipelined architectures for the Viterbi algorithm, Boo, M. ; Brugera, J. D. TENCON '97. IEEE Region 10 Annual Conference. Speech and Image Technologies for Computing and Telecommunications. , Proceedings of IEEE , Volume: 1 , 1997 Page(s): 239 -242 vol. z [9]. A high speed Viterbi decoder using path limited PRML method and its application to 1/2 inch HD full bit rate digital VCR, Hara, M. ; Yoshinaka, T. ; Sugizaki, Y. ; Ohura, S. Consumer Electronics, 2000. ICCE. 2000 Digest of Technical Papers. Page(s): 96 -97 z [10]. Novel Viterbi decoder VLSI implementation and its performance, Kubota, S. ; Kato, S. ; Ishitani, T. Communications, IEEE Transactions on, Volume: 41 Issue: 8 , Aug. 1993 Page(s): 1170 – 1178 z [11], "A 1 -Gb/s, four-state, sliding block Viterbi decoder, " P. J. Black, T. H. -Y. Meng, IEEE J. Solid-State Circuits, vol. 32, no. 6, June 1997, pp. 797 -805