Viterbi algorithm finds most probable sequence of states

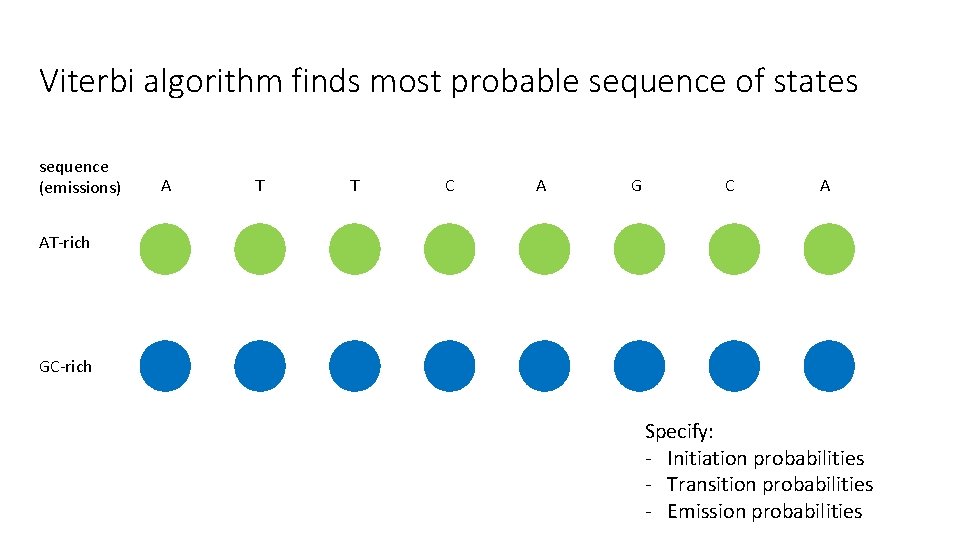
Viterbi algorithm finds most probable sequence of states sequence (emissions) A T T C A G C A AT-rich GC-rich Specify: - Initiation probabilities - Transition probabilities - Emission probabilities

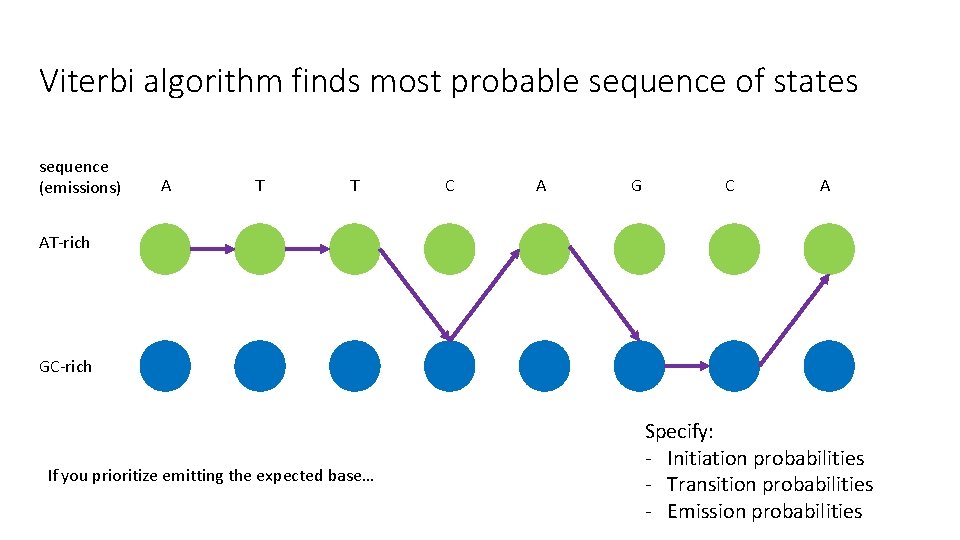
Viterbi algorithm finds most probable sequence of states sequence (emissions) A T T C A G C A AT-rich GC-rich If you prioritize emitting the expected base… Specify: - Initiation probabilities - Transition probabilities - Emission probabilities

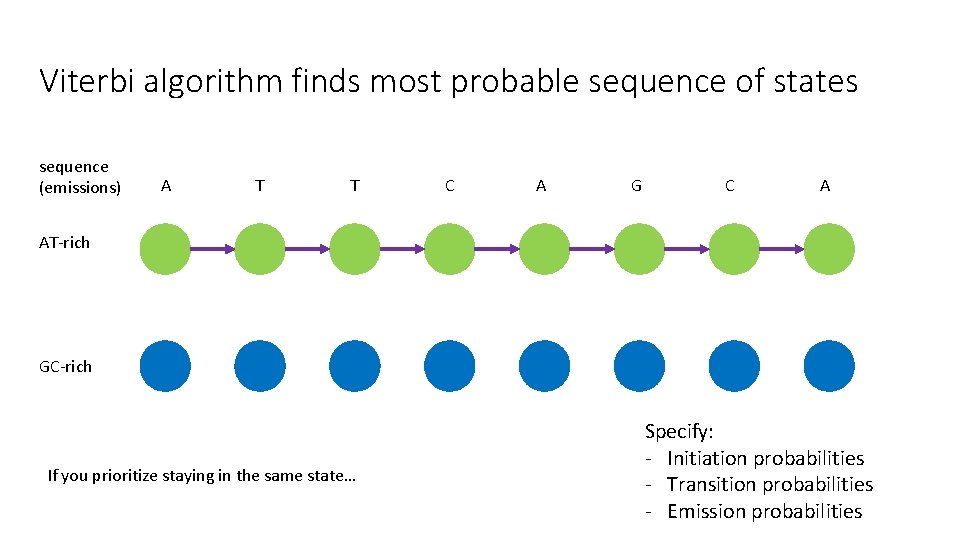
Viterbi algorithm finds most probable sequence of states sequence (emissions) A T T C A G C A AT-rich GC-rich If you prioritize staying in the same state… Specify: - Initiation probabilities - Transition probabilities - Emission probabilities

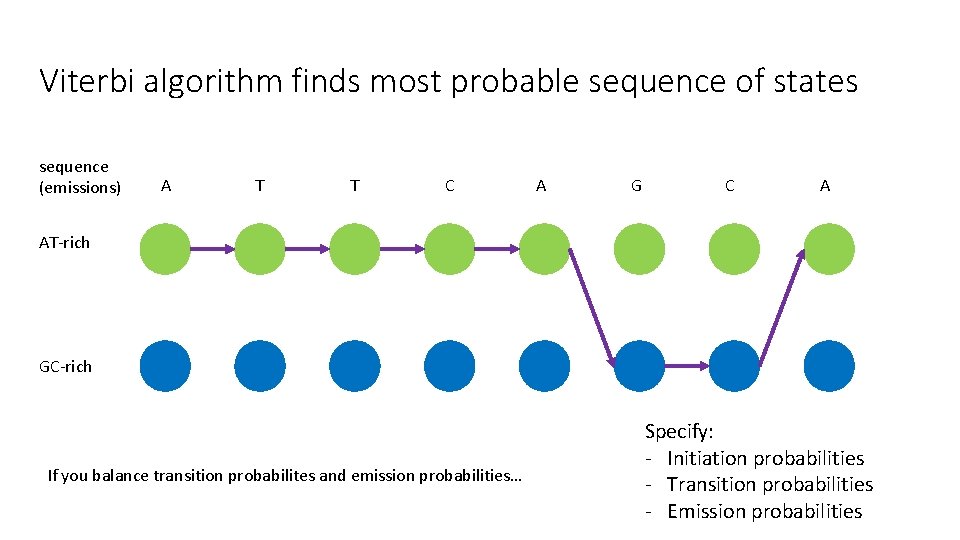
Viterbi algorithm finds most probable sequence of states sequence (emissions) A T T C A G C A AT-rich GC-rich If you balance transition probabilites and emission probabilities… Specify: - Initiation probabilities - Transition probabilities - Emission probabilities

Viterbi algorithm • Dynamic programming • At sequence position i, store the probability of the most probable sequence of states from 1 to i • Find sequence of states that result in highest probability of final state by following back pointers

Updating transition probabilites 10 times 1. Find most probable path with Viterbi algorithm 2. Calculate how often transitions happen between all pairs of states 3. Set the transition probabilities to those frequencies

HW 5 tips • Calculate first few steps by hand make sure your program matches (exactly!) • Create other small test cases • Avoid underflow • Take the logarithm • Then add instead of multiply • See Mann and Rabiner (pg 273) for more details [links on website] • Need to deal with log(0)

HW 4 analysis

HW 4 analysis • Plot • Frequency/weight matrices, sequence logo • Histograms of scores at CDS and non-CDS sites • Are the scores for CDS and non-CDS sites different?

Bootstrapping example: Does the probability of getting heads when flipping a coin exceed 0. 50? Flip a coin 10 times: 0123456789 HTHHTHHTTH Sample with replacement: 0625172330 HHHHTTHHHH Calculate probability of getting heads for the sample: P(H) = 0. 80

Bootstrapping example: Does the probability of getting heads when flipping a coin exceed 0. 50? Flip a coin 10 times: 0123456789 HTHHTHHTTH Sample with replacement: 0625172330 HHHHTTHHHH Calculate probability of getting heads for the sample: P(H) = 0. 80

Bootstrapping example: Does the probability of getting heads when flipping a coin exceed 0. 50? Flip a coin 10 times: 0123456789 HTHHTHHTTH Sample with replacement: 0625172330 HHHHTTHHHH Calculate probability of getting heads for the sample: P(H) = 0. 80 Resample a bunch of times and store number of heads for each. Probability of getting heads is greater than 0. 50 if the observed probability is greater than 0. 50 in at least 95% of bootstrap estimates.