Visualizing Prims MST Algorithm Used to Trace the

Visualizing Prim’s MST Algorithm Used to Trace the Algorithm in Class There are Slight Changes From the Code These Slides are not Complete

Example – MST (Prim’s Algorithm) • Assume a connected graph has nodes labeled by some identifying letter or number, arcs which are non-directional and have positive weights associated with them. • The MST problem is to find a minimum spanning tree. 2

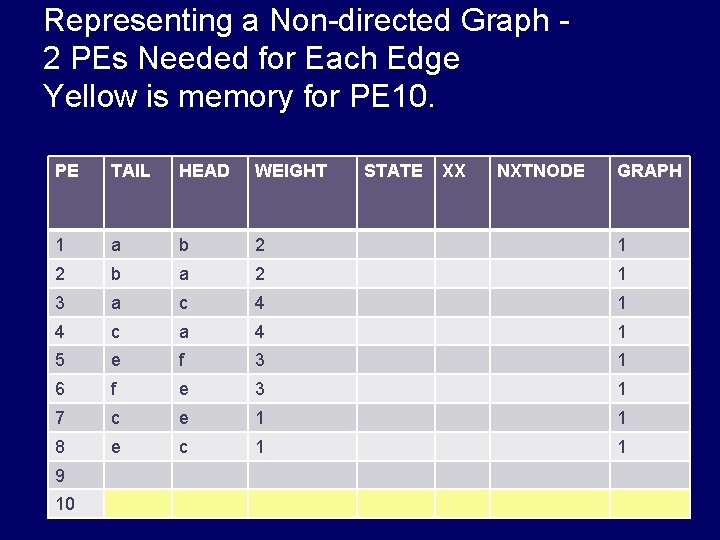
Representing a Non-directed Graph 2 PEs Needed for Each Edge Yellow is memory for PE 10. PE TAIL HEAD WEIGHT STATE XX NXTNODE GRAPH 1 a b 2 1 2 b a 2 1 3 a c 4 1 4 c a 4 1 5 e f 3 1 6 f e 3 1 7 c e 1 1 8 e c 1 1 9 10 3

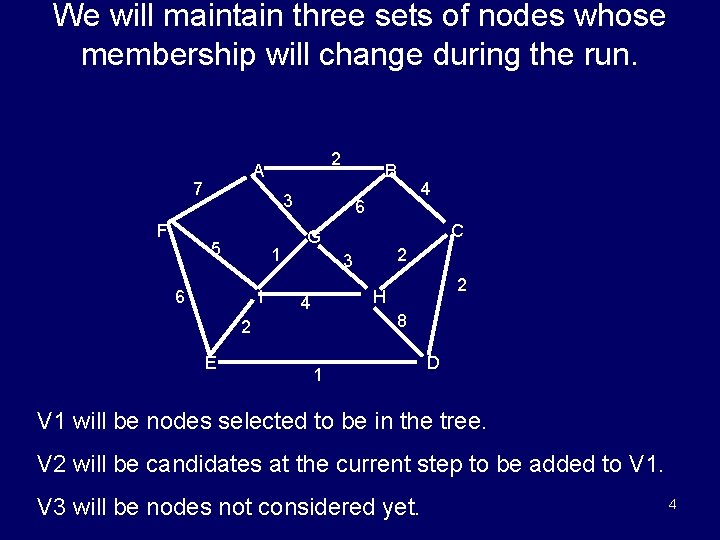
We will maintain three sets of nodes whose membership will change during the run. 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D V 1 will be nodes selected to be in the tree. V 2 will be candidates at the current step to be added to V 1. V 3 will be nodes not considered yet. 4

Colors Used in Graphic Visualization V 1 nodes and their selected edges will be in red. V 2 nodes with their candidate edges will be in blue. V 3 nodes and all other edges will remain white. 5

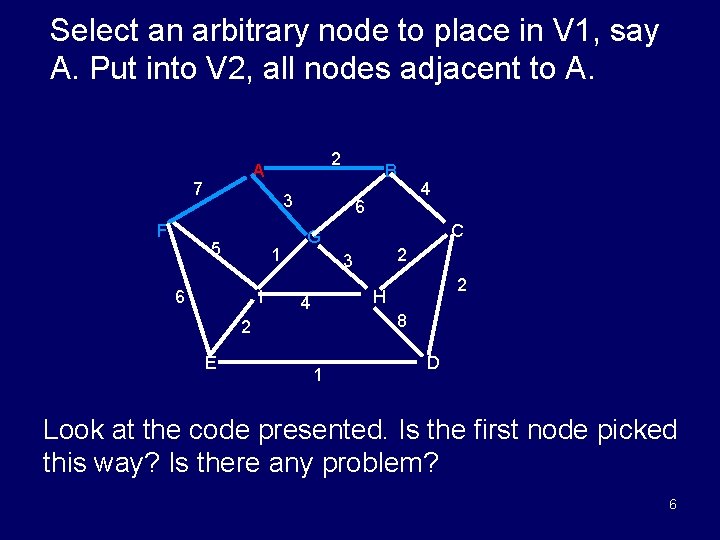
Select an arbitrary node to place in V 1, say A. Put into V 2, all nodes adjacent to A. 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Look at the code presented. Is the first node picked this way? Is there any problem? 6

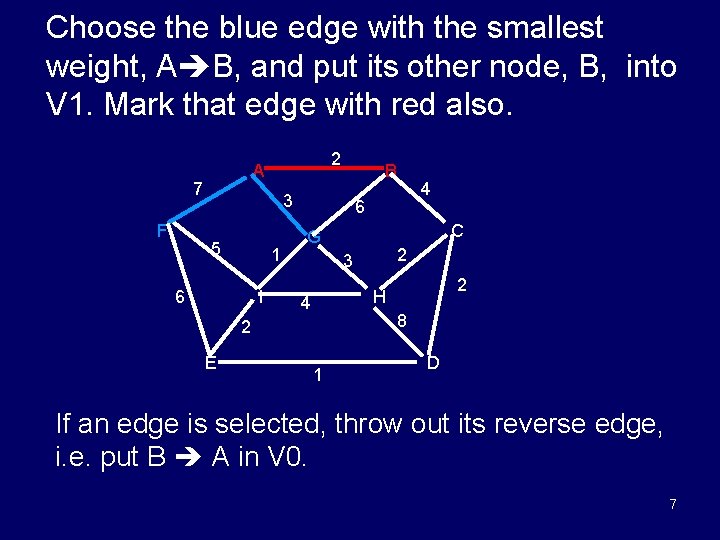
Choose the blue edge with the smallest weight, A B, and put its other node, B, into V 1. Mark that edge with red also. 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D If an edge is selected, throw out its reverse edge, i. e. put B A in V 0. 7

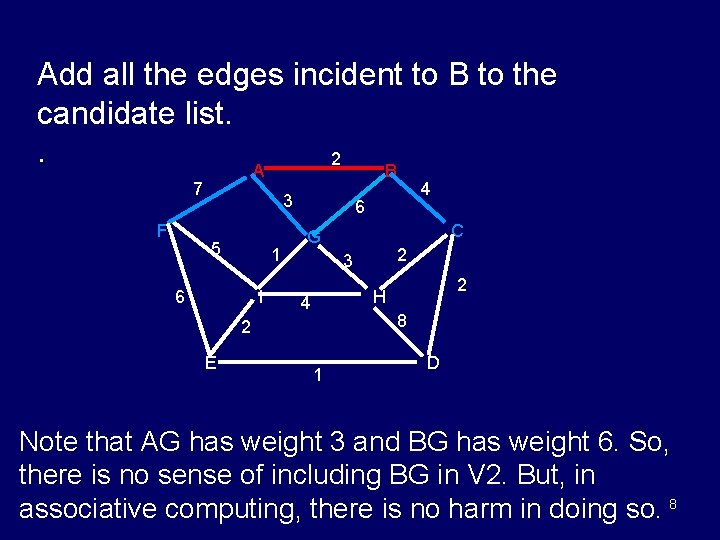
Add all the edges incident to B to the candidate list. . 2 A B 7 F 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Note that AG has weight 3 and BG has weight 6. So, there is no sense of including BG in V 2. But, in associative computing, there is no harm in doing so. 8

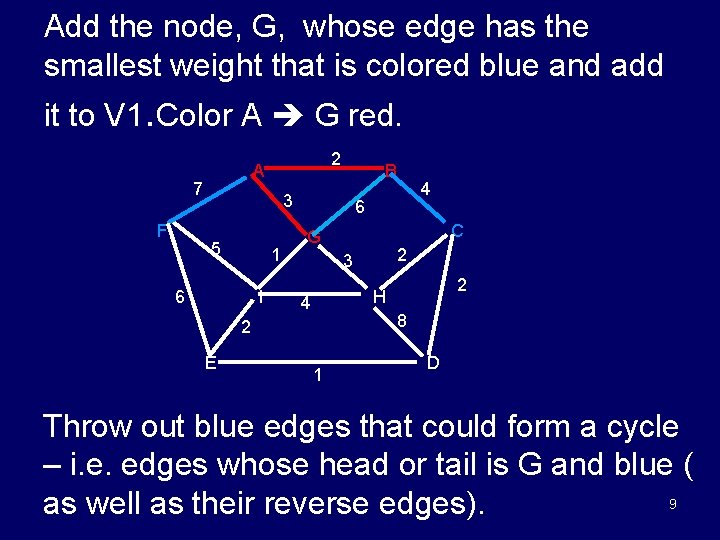
Add the node, G, whose edge has the smallest weight that is colored blue and add it to V 1. Color A G red. 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Throw out blue edges that could form a cycle – i. e. edges whose head or tail is G and blue ( 9 as well as their reverse edges).

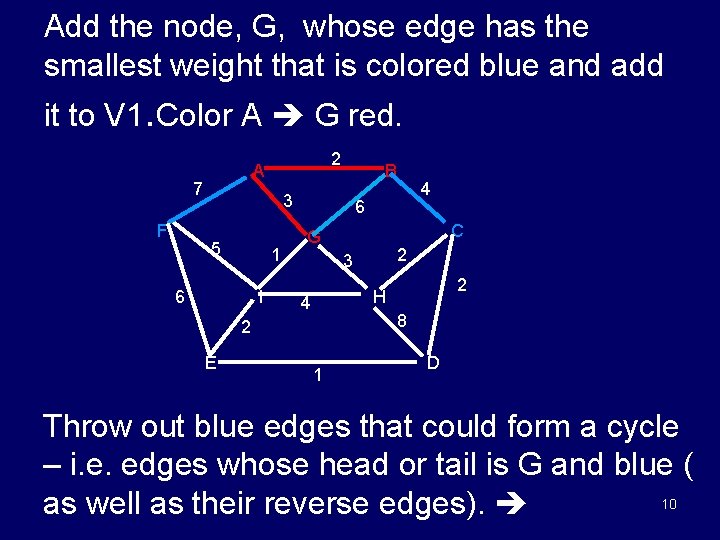
Add the node, G, whose edge has the smallest weight that is colored blue and add it to V 1. Color A G red. 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Throw out blue edges that could form a cycle – i. e. edges whose head or tail is G and blue ( 10 as well as their reverse edges).

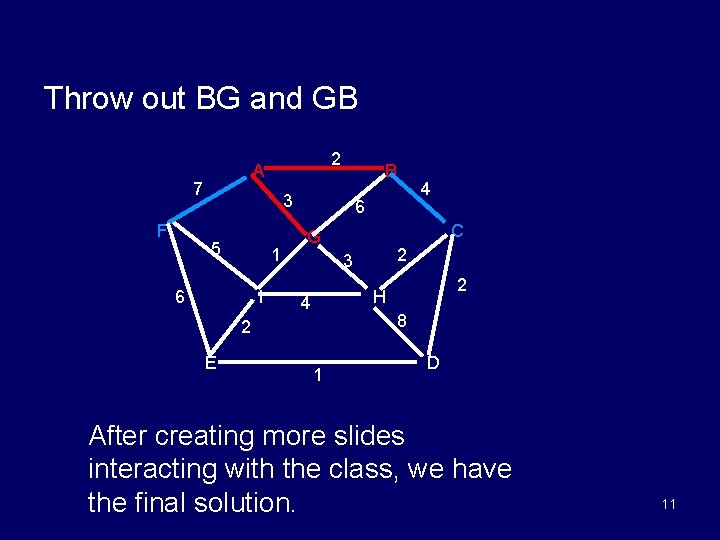
Throw out BG and GB 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D After creating more slides interacting with the class, we have the final solution. 11

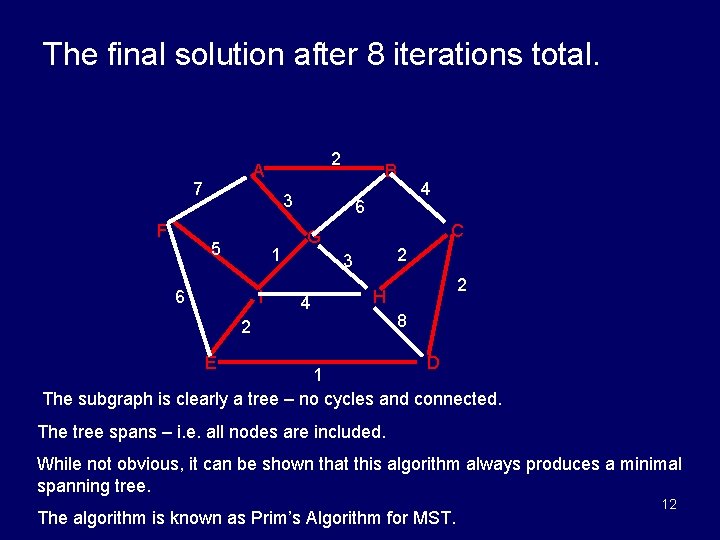
The final solution after 8 iterations total. 7 F 2 A B 3 5 1 6 I 4 6 C G 2 3 4 2 H 2 8 E D 1 The subgraph is clearly a tree – no cycles and connected. The tree spans – i. e. all nodes are included. While not obvious, it can be shown that this algorithm always produces a minimal spanning tree. The algorithm is known as Prim’s Algorithm for MST. 12