Visualizing Algebraic Relationships Solving Rate Problems with Pattern

Visualizing Algebraic Relationships: Solving Rate Problems with Pattern Blocks Dianna Spence Robb Sinn North Georgia College & State University Joint Mathematics Meetings 2010

Introduction Course: Modeling in Algebra l Students: K-8 pre-service teachers l Sample Problem: Combined work rate problem l Joe and Matt start a landscaping business together. Homes in their neighborhood have similarlysized lawns. Typically, Joe can mow a lawn and trim all the shrubs in 3 hours. Matt usually needs 2 hours to do the same job. They decide to work together on 5 lawns. How long should it take them to finish?

Instructional Strategy l Ensure students are familiar with pattern blocks l Pose a combined rate problem and suggest modeling the problem with pattern blocks l Guided discovery

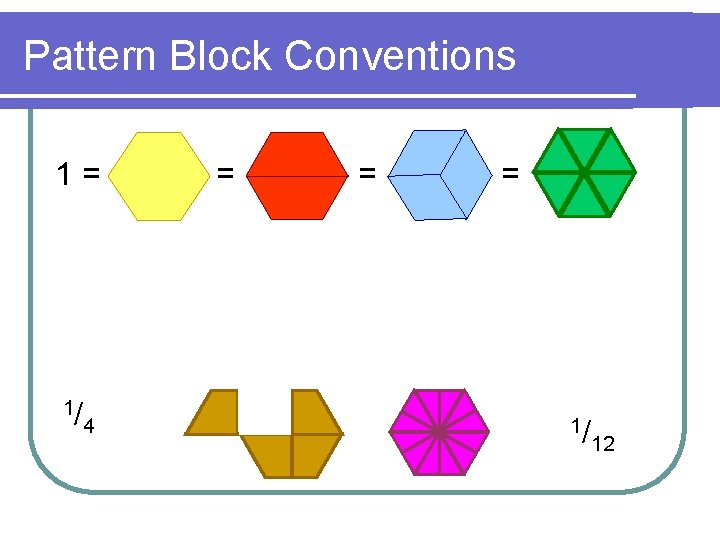
Pattern Block Conventions 1= = = 1/ 1/ 4 2 = 1/ 3 1/ 1/ 6 12

Recall Sample Problem Joe and Matt start a landscaping business together. Homes in their neighborhood have similarlysized lawns. Typically, Joe can mow a lawn and trim all the shrubs in 3 hours. Matt usually needs 2 hours to do the same job. They decide to work together on 5 lawns. How long should it take them to finish?

Rate Representation Joe: 3 hours for 1 lawn Matt: 2 hours for 1 lawn Joe Matt Hour: 1 2 3

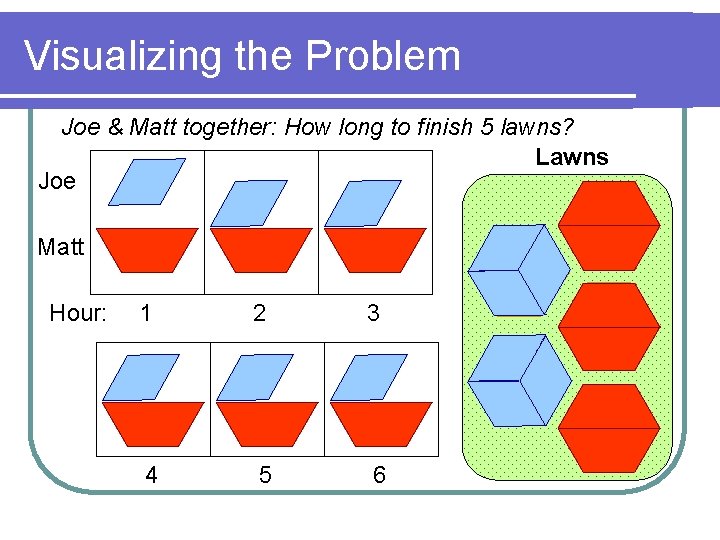
Visualizing the Problem Joe & Matt together: How long to finish 5 lawns? Lawns Joe Matt Hour: 1 2 3 4 5 6

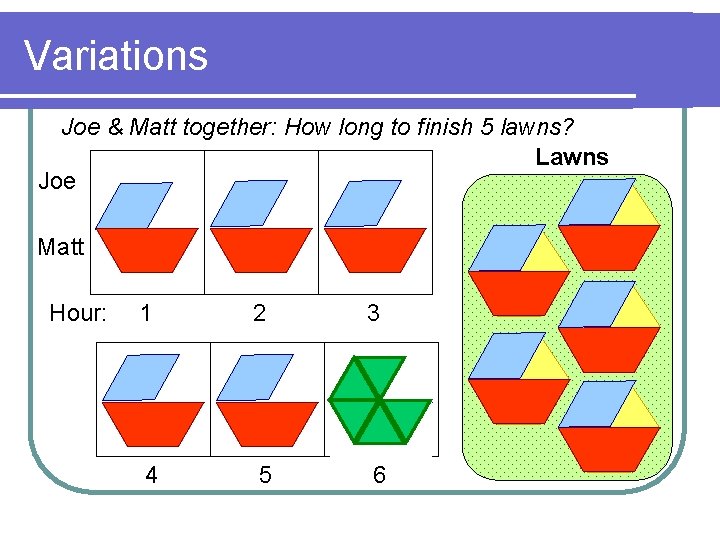
Variations Joe & Matt together: How long to finish 5 lawns? Lawns Joe Matt Hour: 1 2 3 4 5 6

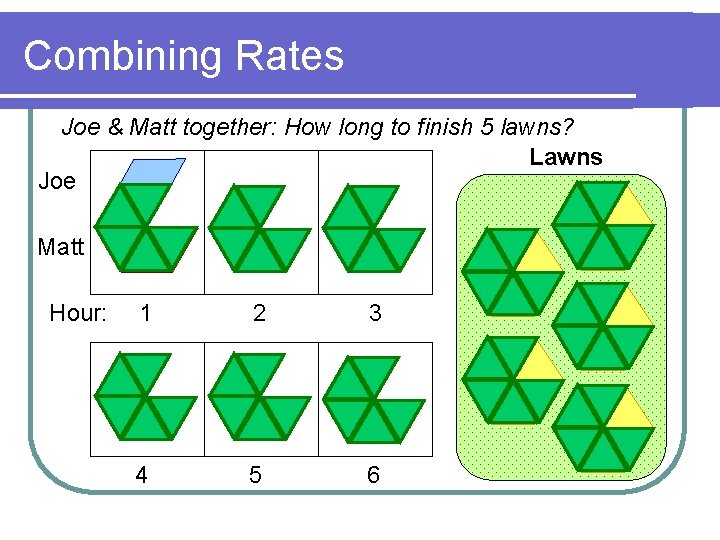
Combining Rates Joe & Matt together: How long to finish 5 lawns? Lawns Joe Matt Hour: 1 2 3 4 5 6

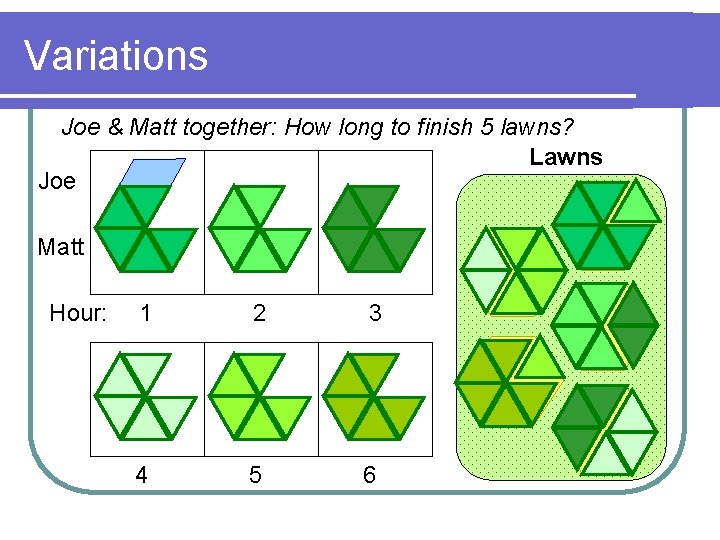
Variations Joe & Matt together: How long to finish 5 lawns? Lawns Joe Matt Hour: 1 2 3 4 5 6

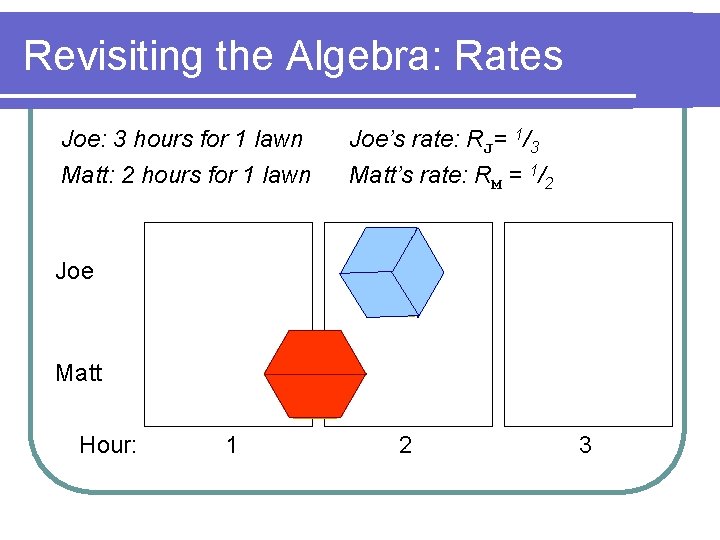
Revisiting the Algebra: Rates Joe: 3 hours for 1 lawn Matt: 2 hours for 1 lawn Joe’s rate: RJ= 1/3 Matt’s rate: RM = 1/2 Joe Matt Hour: 1 2 3

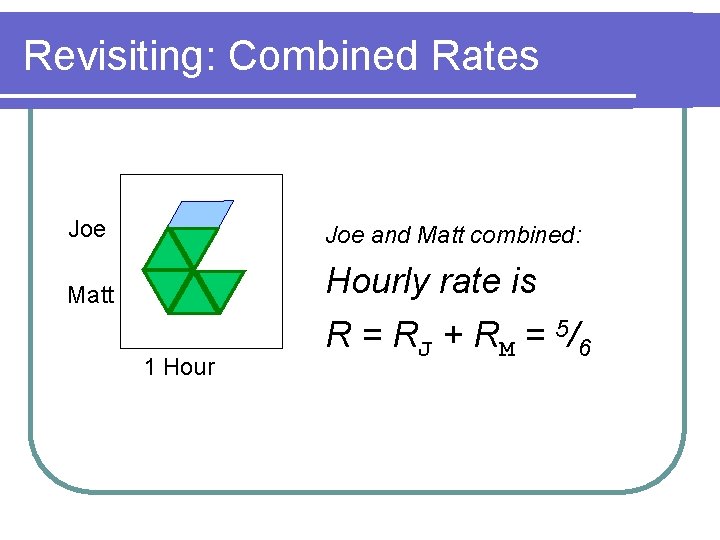
Revisiting: Combined Rates Joe and Matt combined: Matt 1 Hourly rate is R = R J + R M = 5/ 6

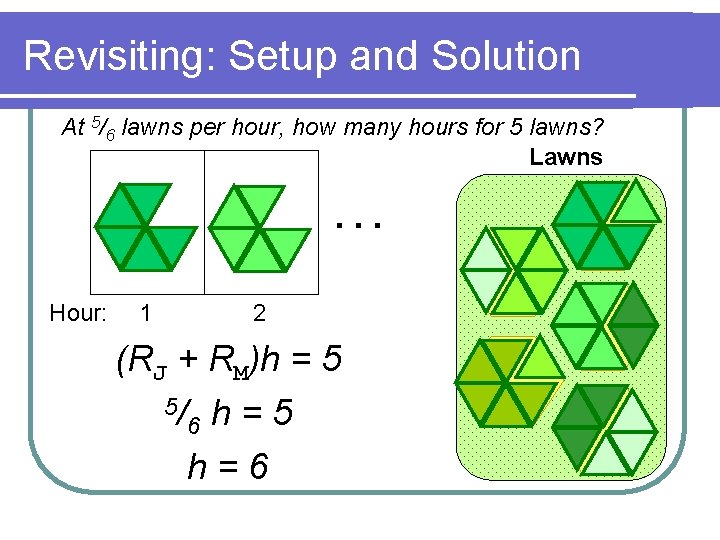
Revisiting: Setup and Solution At 5/6 lawns per hour, how many hours for 5 lawns? Lawns … Hour: 2 1 (RJ + RM)h = 5 5/ h=5 h=6 6

Extending the Reasoning Maria and Dusti are decorating the gym with helium balloons. Maria can inflate and tie off 2 balloons every 3 minutes. Dusti requires 2 minutes to finish 1 balloon. Working together, how long will it take them have a batch of 35 balloons ready?

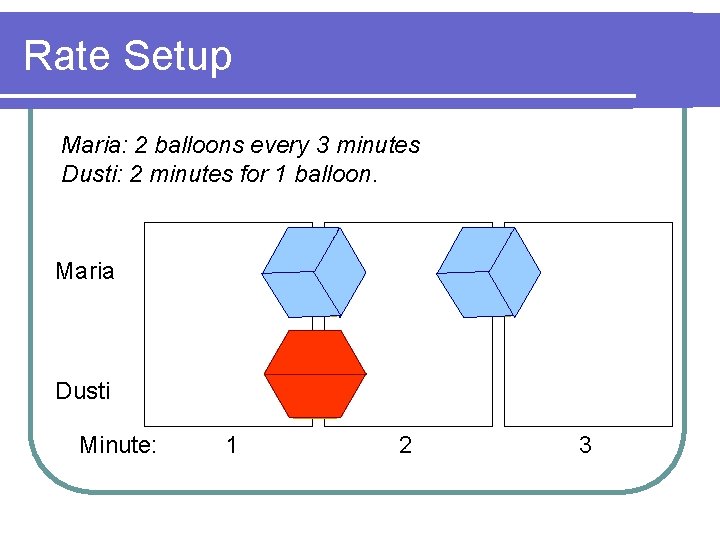
Rate Setup Maria: 2 balloons every 3 minutes Dusti: 2 minutes for 1 balloon. Maria Dusti Minute: 1 2 3

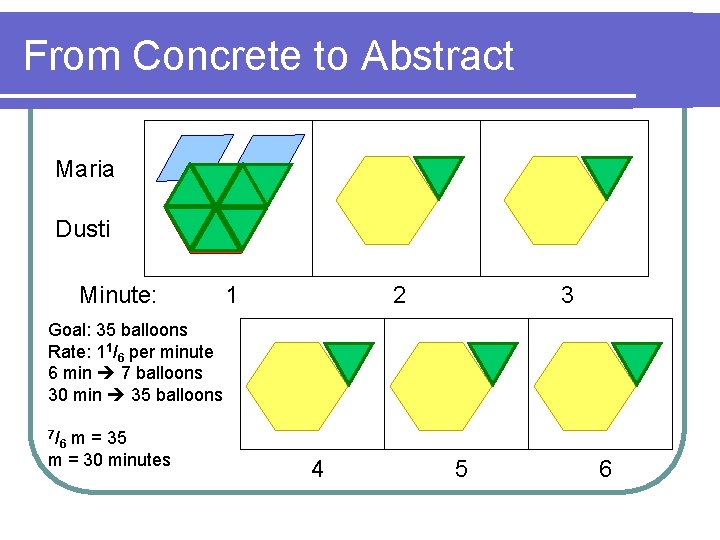
From Concrete to Abstract Maria Dusti Minute: 1 2 3 Goal: 35 balloons Rate: 11/6 per minute 6 min 7 balloons 30 min 35 balloons 7/ m = 35 m = 30 minutes 6 4 5 6

Extending & Generalizing Progression: l Situations with fractional answer (e. g. , 7½ minutes) l Change of question: “How many lawns could they mow in 9 hours? ” l Situations with fractions that don’t lend themselves to pattern blocks l Students draw their own pictures

Does This Technique “Work”? Research Design l Control: Classes received traditional procedural instruction only (n = 26) l Experimental: Classes used manipulative discovery technique (n = 49) Data Collection l Pre-test l Post-test (immediately after instruction) l Retest (6 weeks after instruction)

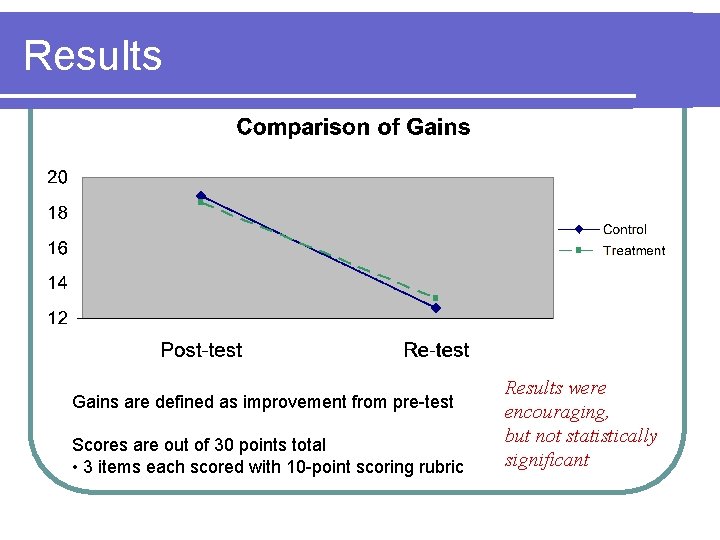
Results Gains are defined as improvement from pre-test Scores are out of 30 points total • 3 items each scored with 10 -point scoring rubric Results were encouraging, but not statistically significant

Final Notes Mitigating Factors l Relatively small samples l Very limited instruction time (1 class period) l l Not enough time for full discovery Insufficient followup: generalizing, formalizing Our Interpretation l Method shows potential, especially to improve long-term outcomes l A better trial is warranted

Questions