Visualization of graphs using their product structure Bla

Visualization of graphs using their product structure Blaž Zmazek and Janez Žerovnik FME University of Maribor and IMFM Koper, 18. nov. 2005 1

Introduction l Knowledge of the structure of a graph 1. Faster algorithms for solving problems (Examples: chromatic number, …) 2. Visualization of the graph l Graph drawing l … l CLAIM: if known, structural properties can help EXAMPLE: graph products and bundles l Koper, 18. nov. 2005 (conferences, competitions, …) 2

References l Graph drawing … vast literature, Batagelj and Mrvar won 2005 competition at Graph Drawing …. l Graph products Imrich, Klavžar: Product Graphs, structure and recognition, Wiley 2000. … l Graph bundles Pisanski, Shawe-Taylor, Vrabec : JCT (B) 1983 …. Less studied, some recent results by Pisanski, Imrich, Zmazek, Žerovnik, … … Koper, 18. nov. 2005 3

Definitions Graph l Graph products: l l Cartesian l Direct l Strong l Lexicographic Koper, 18. nov. 2005 4

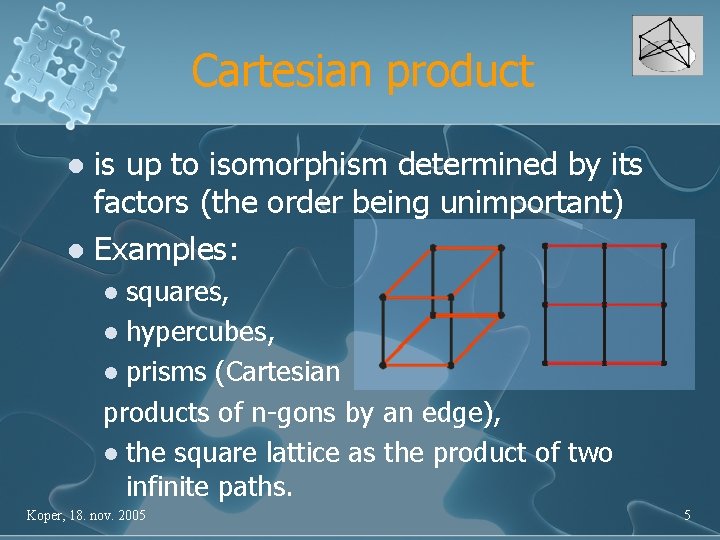
Cartesian product is up to isomorphism determined by its factors (the order being unimportant) l Examples: l squares, l hypercubes, l prisms (Cartesian products of n-gons by an edge), l the square lattice as the product of two infinite paths. l Koper, 18. nov. 2005 5

Cartesian product l All finite connected graphs have unique prime factorizations with respect to the Cartesian product l Product relation (Sabidussi) = l Djoković + local product relation (lpr) convex hull of the lpr … l recognition in polynomial time l l Koper, 18. nov. 2005 6

Applications of Cartesian product l Hamming graphs used in coding theory l and median graphs are isometric subgraphs of Cartesian products l l their l design of interconnection networks l l recognition is fast Hypercubes Reconstruction of a Cartesian product l the problem is polynomial Koper, 18. nov. 2005 7

Other products l Direct product : l The set of edges of the strong product is the union of edges of Cartesian product and edges of direct product. polynomial algorithm for recognition (Imrich) algorithm for recognition (Feigenbaum at al. ) l Feigenbaum and Schaffer: the problem of recognizing composite graphs with respect to the lexicographic product is equivalent to testing graph isomorphism Koper, 18. nov. 2005 8

(Cartesian) graph bundle Koper, 18. nov. 2005 9

Graph bundles l generalize the notion of covering graphs (NP-hard recognition) l graph products l more than one presentation of graph as a graph bundle may exist l Cartesian and strong bundles with totally disconnected fibre l covering graphs Koper, 18. nov. 2005 10

Cartesian graph bundle l All presentations can be found in polynomial time for a Cartesian graph bundle over base graph with at least one minimal presentation with fibre different from K 2 [Zmazek, Žerovnik] l There is a polynomial algorithm for recognizing Cartesian graph bundles over l l l triangle-free base, triangles disjoint in base and K 4 e-free base Koper, 18. nov. 2005 11

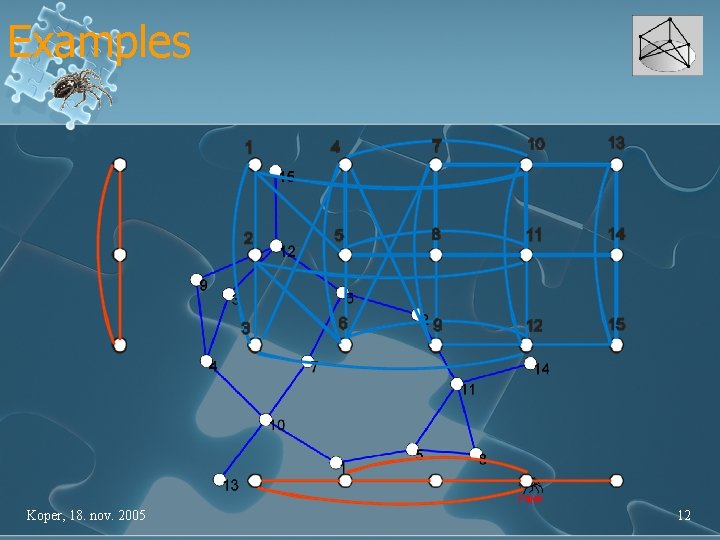
Examples Koper, 18. nov. 2005 12

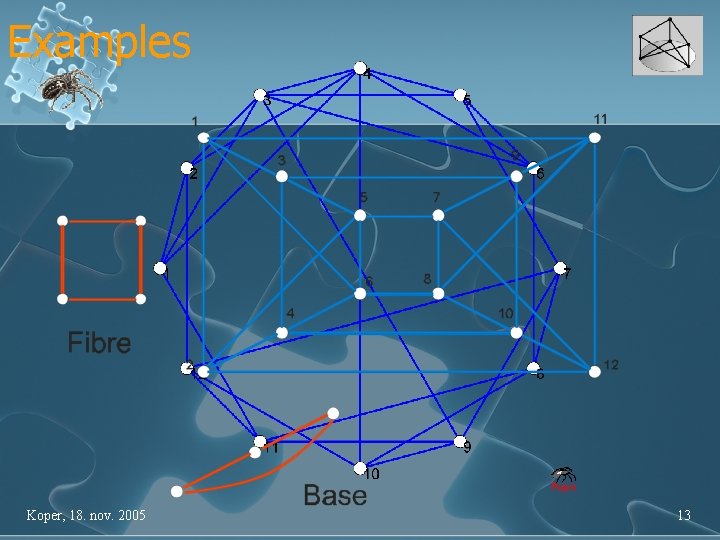
Examples Koper, 18. nov. 2005 13

Koper, 18. nov. 2005 14