Visualization Fundamentals Interpolation Functions Basic 2 D Scalar

Visualization Fundamentals • Interpolation Functions • Basic 2 D Scalar Data Visualization Techniques – Color Maps – High Fields – Contours

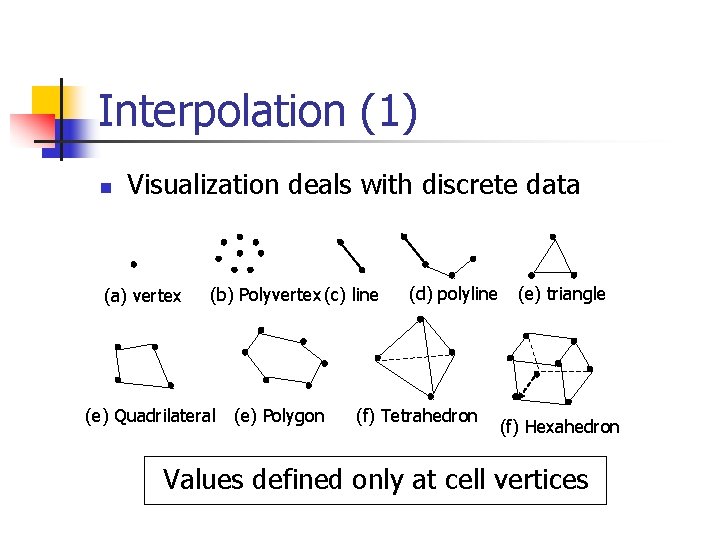
Interpolation (1) n Visualization deals with discrete data (a) vertex (b) Polyvertex (c) line (e) Quadrilateral (e) Polygon (d) polyline (f) Tetrahedron (e) triangle (f) Hexahedron Values defined only at cell vertices

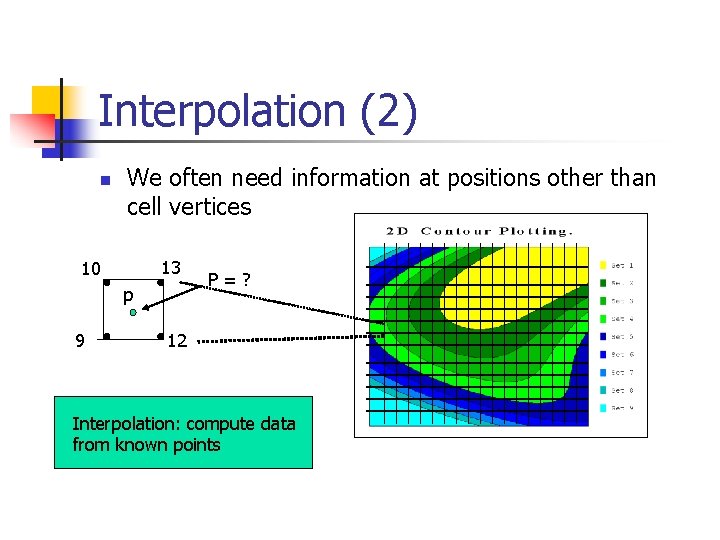
Interpolation (2) n We often need information at positions other than cell vertices 13 10 p 9 P=? 12 Interpolation: compute data from known points

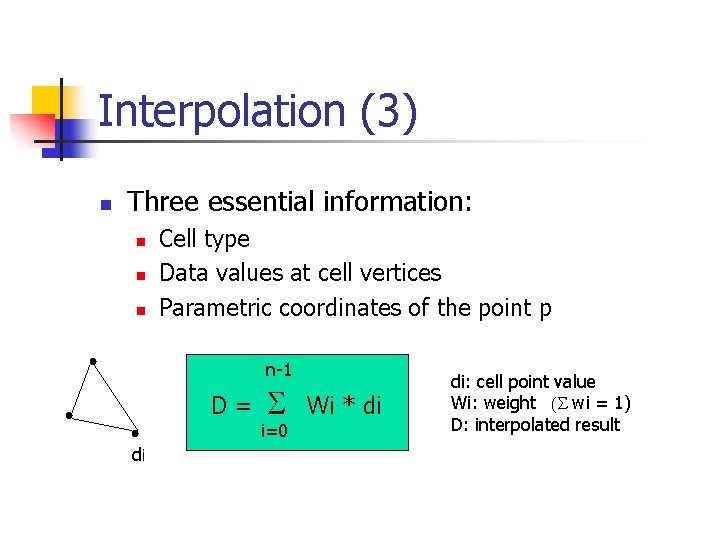
Interpolation (3) n Three essential information: n n n Cell type Data values at cell vertices Parametric coordinates of the point p n-1 D= di S i=0 Wi * di di: cell point value Wi: weight (S wi = 1) D: interpolated result

Interpolation (4) Parametric Coordinates: Used to specify the location of a point within a cell r=1 r=0 d 1 r 0 <= r <=1 (a) line W 0 = (1 -r) W 1 = r n-1 D= S i=0 Wi * di

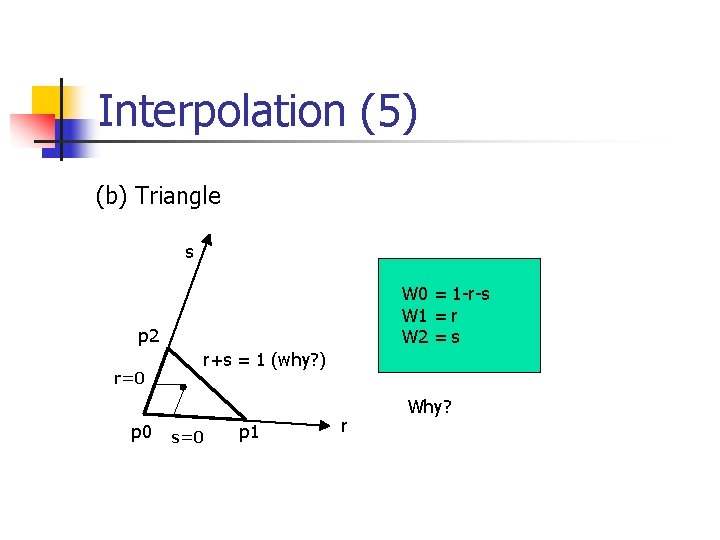
Interpolation (5) (b) Triangle s W 0 = 1 -r-s W 1 = r W 2 = s p 2 r+s = 1 (why? ) r=0 p 0 s=0 p 1 r Why?

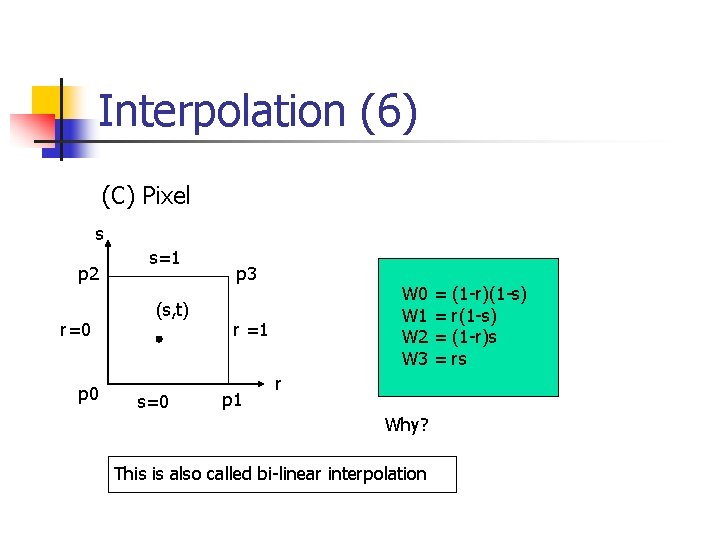
Interpolation (6) (C) Pixel s p 2 r=0 p 0 s=1 (s, t) s=0 p 3 W 0 W 1 W 2 W 3 r =1 p 1 r Why? This is also called bi-linear interpolation = = (1 -r)(1 -s) r(1 -s) (1 -r)s rs

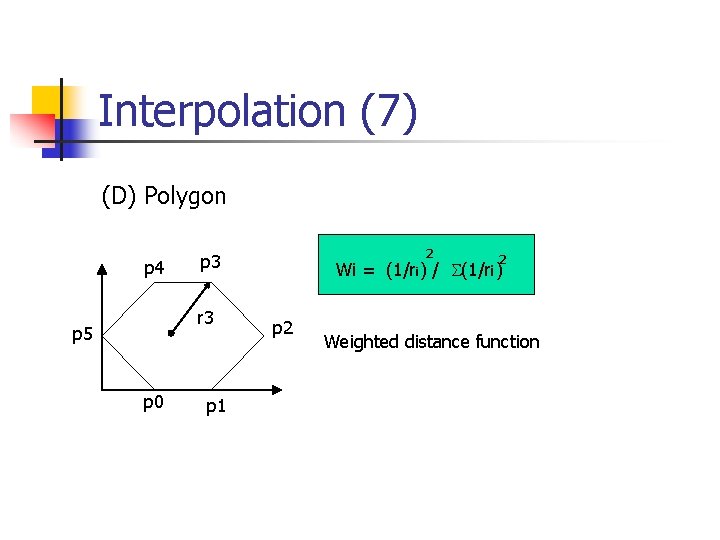
Interpolation (7) (D) Polygon p 4 r 3 p 5 p 0 2 p 3 p 1 2 Wi = (1/ri) / S(1/ri) p 2 Weighted distance function

Interpolation (8) (D) Tetrahedron t s p 3 W 0 W 1 W 2 W 3 p 2 p 0 p 1 r = = 1 -r-s-t r s t

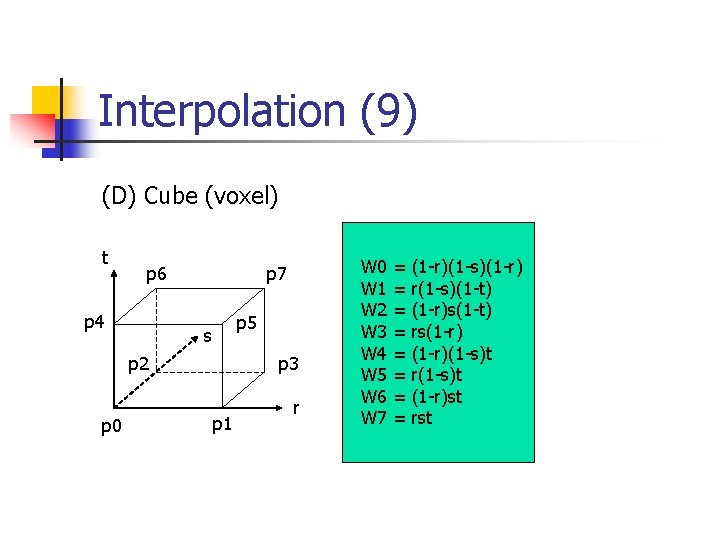
Interpolation (9) (D) Cube (voxel) t p 6 p 4 p 7 p 5 s p 2 p 0 p 3 p 1 r W 0 W 1 W 2 W 3 W 4 W 5 W 6 W 7 = = = = (1 -r)(1 -s)(1 -r) r(1 -s)(1 -t) (1 -r)s(1 -t) rs(1 -r)(1 -s)t r(1 -s)t (1 -r)st rst

Interpolation (10) The interpolation function can be used to calculate the geometric position as well. That is, given (r, s, t), calculate the global coordinates Local to global coordinate transformation: n-1 P= S Wi * i=0 Pi

Interpolation (11) How to get (r, s, t) ? • Line, Pixel, Cube are all trivial • Triangle, Tetrahedron can be solved analytically • Qudrilateral or Hexahedra need numerical method n-1 P= S i=0 Wi * Pi Known: P, Pi Unkown: Wi (i. e. r, s, t)

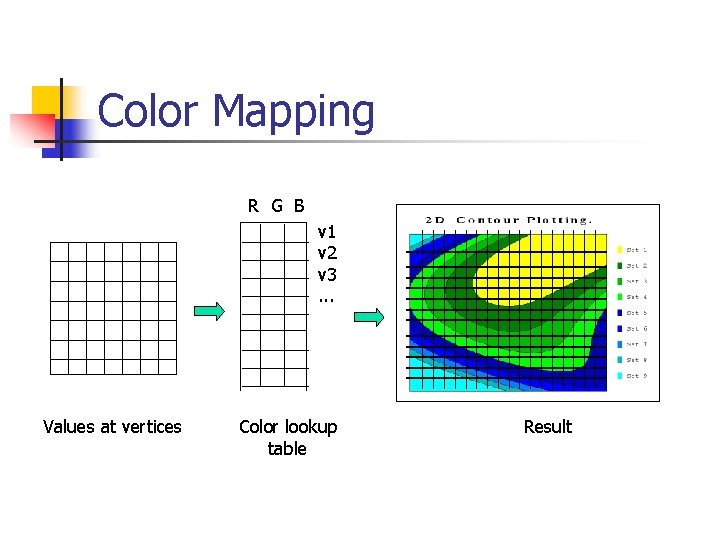
Color Mapping R G B v 1 v 2 v 3. . . Values at vertices Color lookup table Result

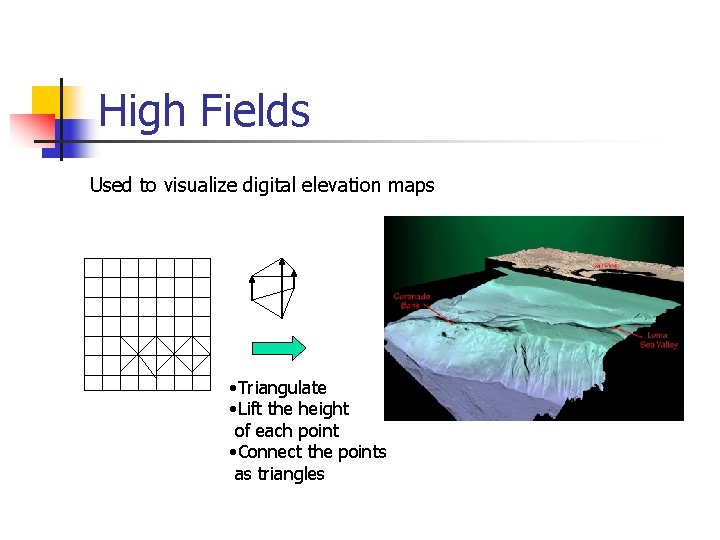
High Fields Used to visualize digital elevation maps • Triangulate • Lift the height of each point • Connect the points as triangles

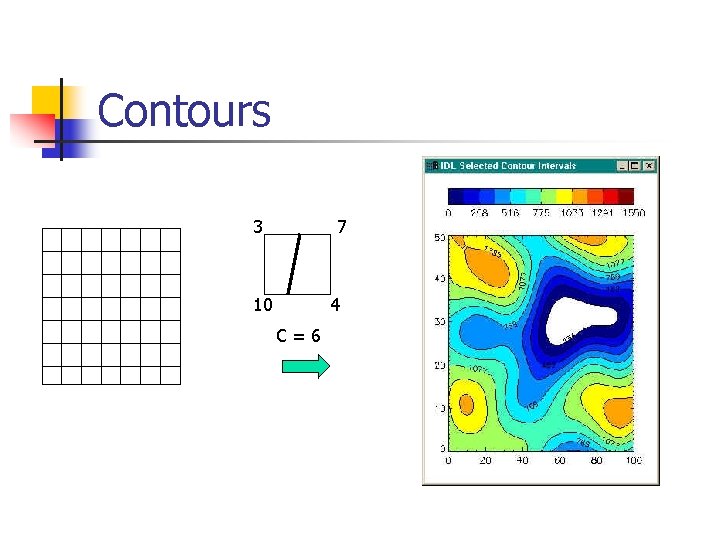
Contours 3 7 10 4 C=6