Visual Computing Lab Product Quantization 2015312521 Noh Haechan

Visual Computing Lab Quantization example (Rule) (0. 0, 1. 0] -> 1 (1. 0, 2. 0] -> 2 (2. 0, 3. 0] -> 3 Then… 2. 437 -> 3

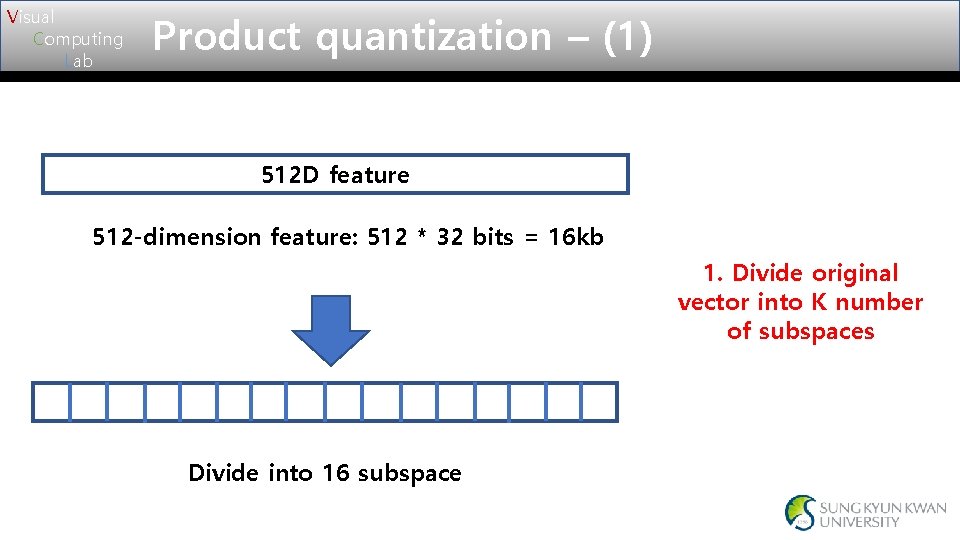
Visual Computing Lab Product quantization – (1) 512 D feature 512 -dimension feature: 512 * 32 bits = 16 kb 1. Divide original vector into K number of subspaces Divide into 16 subspace

Visual Computing Lab Product quantization – (2) Original dimension / number of subspaces = 512 / 16 = 32 dimension per subspace 16 subspace (each 32 dimension)

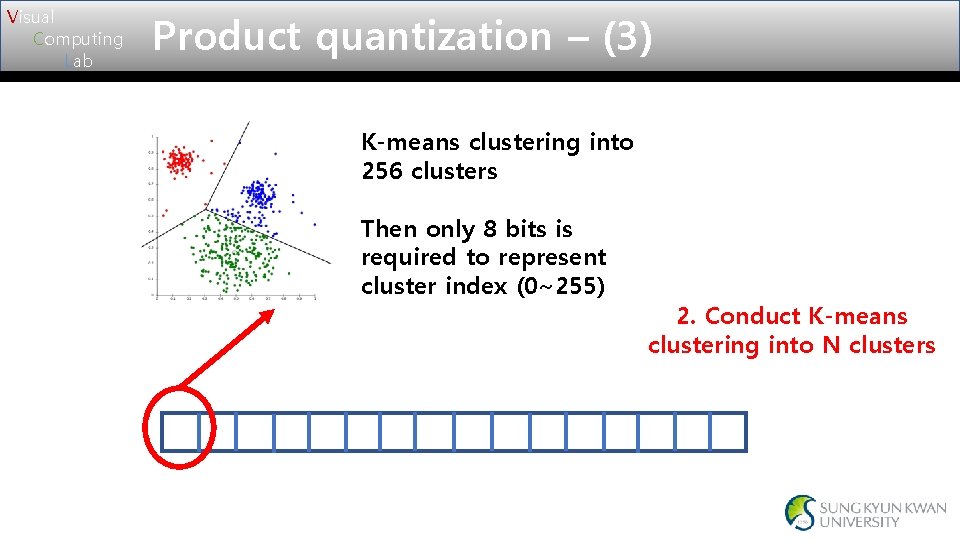
Visual Computing Lab Product quantization – (3) K-means clustering into 256 clusters Then only 8 bits is required to represent cluster index (0~255) 2. Conduct K-means clustering into N clusters

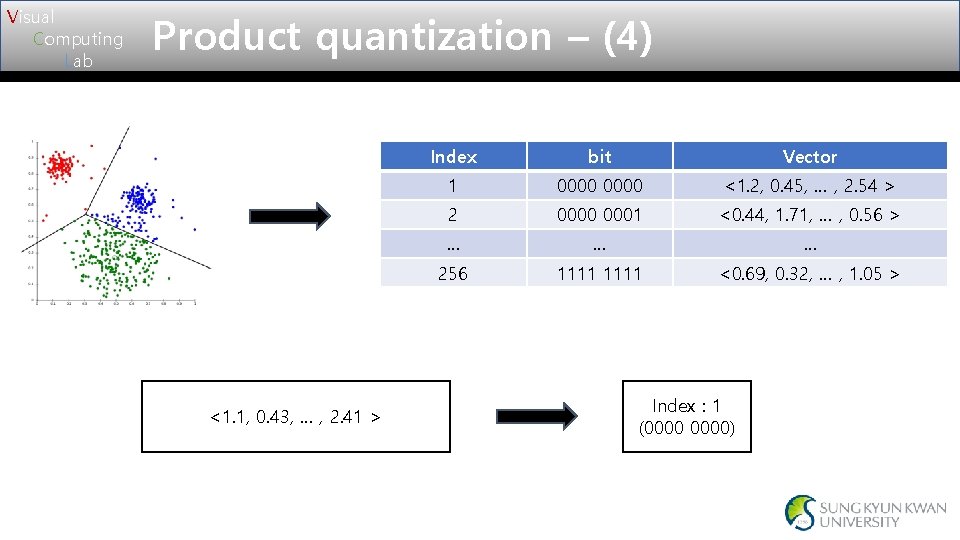
Visual Computing Lab Product quantization – (4) <1. 1, 0. 43, … , 2. 41 > Index bit Vector 1 0000 <1. 2, 0. 45, … , 2. 54 > 2 0000 0001 <0. 44, 1. 71, … , 0. 56 > … … … 256 1111 <0. 69, 0. 32, … , 1. 05 > Index : 1 (0000)

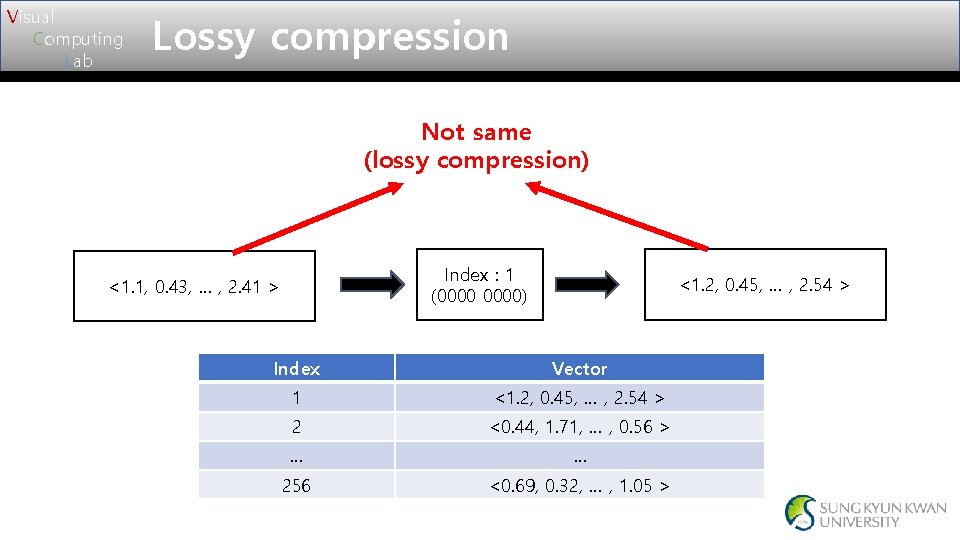
Visual Computing Lab Lossy compression Not same (lossy compression) Index : 1 (0000) <1. 1, 0. 43, … , 2. 41 > <1. 2, 0. 45, … , 2. 54 > Index Vector 1 <1. 2, 0. 45, … , 2. 54 > 2 <0. 44, 1. 71, … , 0. 56 > … … 256 <0. 69, 0. 32, … , 1. 05 >

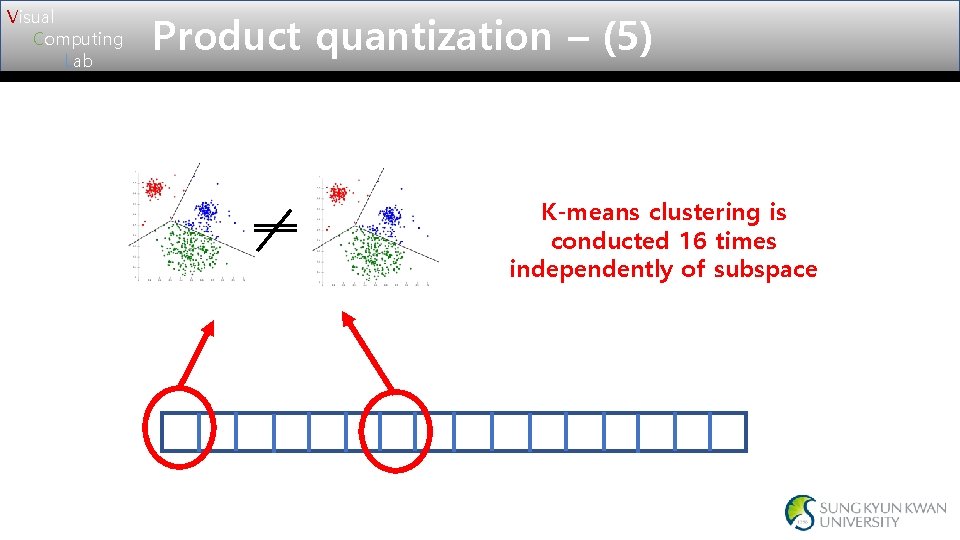
Visual Computing Lab Product quantization – (5) K-means clustering is conducted 16 times independently of subspace

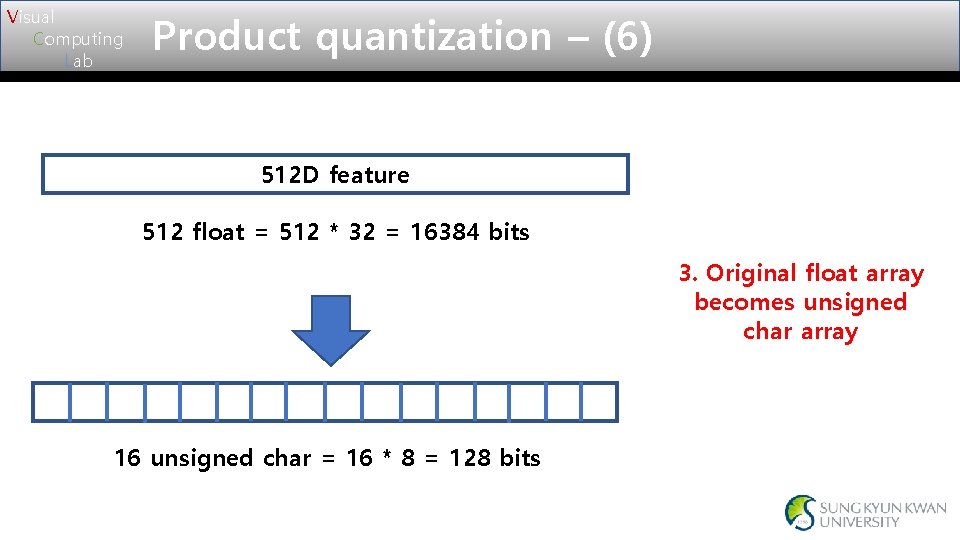
Visual Computing Lab Product quantization – (6) 512 D feature 512 float = 512 * 32 = 16384 bits 3. Original float array becomes unsigned char array 16 unsigned char = 16 * 8 = 128 bits

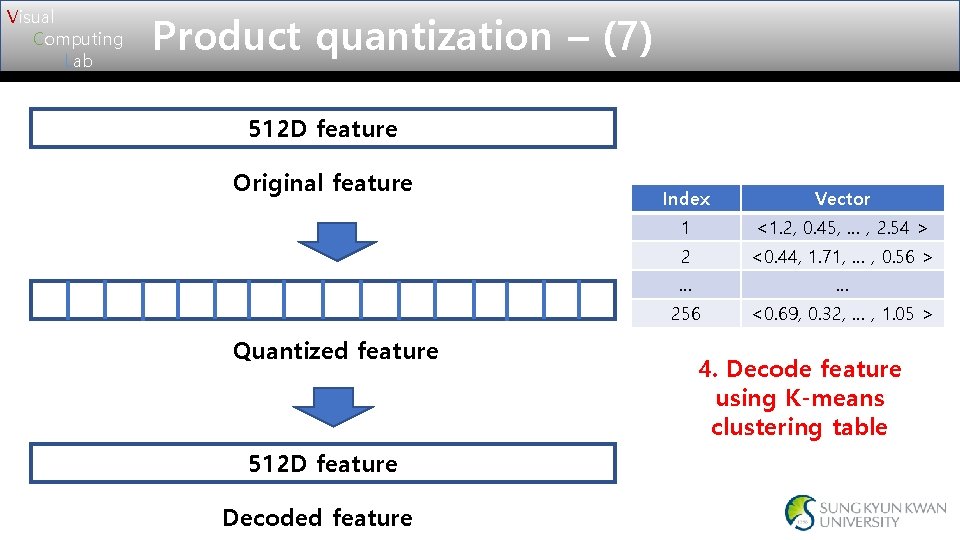
Visual Computing Lab Product quantization – (7) 512 D feature Original feature Quantized feature 512 D feature Decoded feature Index Vector 1 <1. 2, 0. 45, … , 2. 54 > 2 <0. 44, 1. 71, … , 0. 56 > … … 256 <0. 69, 0. 32, … , 1. 05 > 4. Decode feature using K-means clustering table

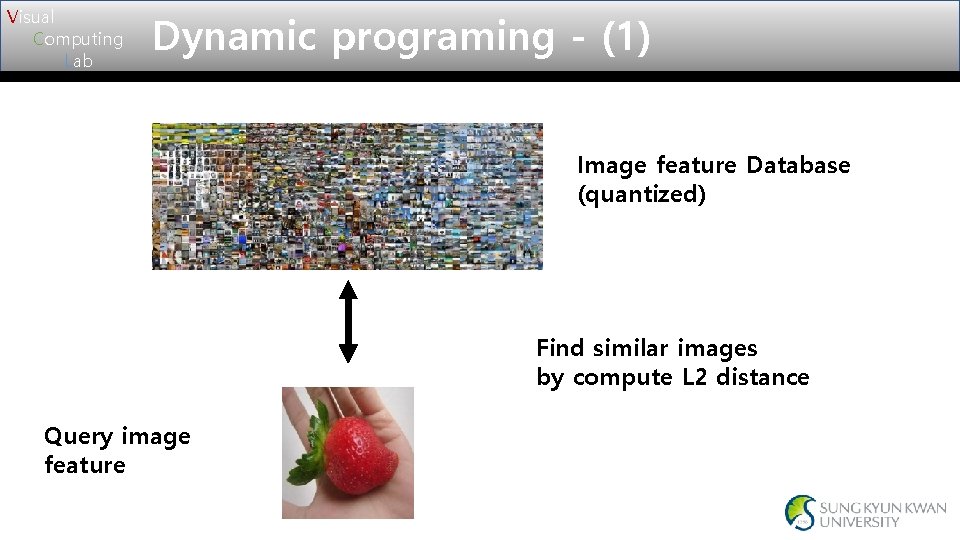
Visual Computing Lab Dynamic programing - (1) Image feature Database (quantized) Find similar images by compute L 2 distance Query image feature

Visual Computing Lab Dynamic programing - (2) Method 1 Compute L 2 distance for all DB Method 2 Compute L 2 distance for all K-means centers once, and reuse it Very slow Fast !!

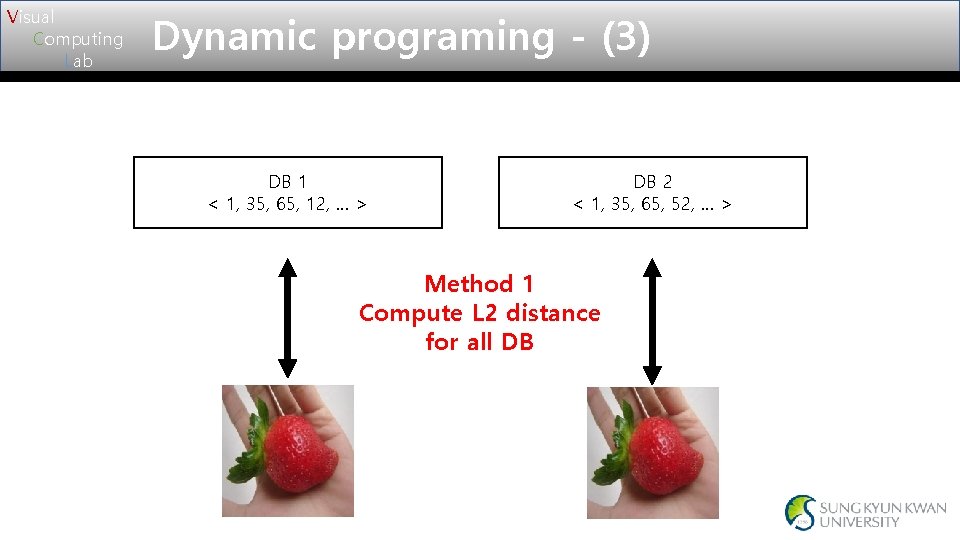
Visual Computing Lab Dynamic programing - (3) DB 1 < 1, 35, 65, 12, … > DB 2 < 1, 35, 65, 52, … > Method 1 Compute L 2 distance for all DB

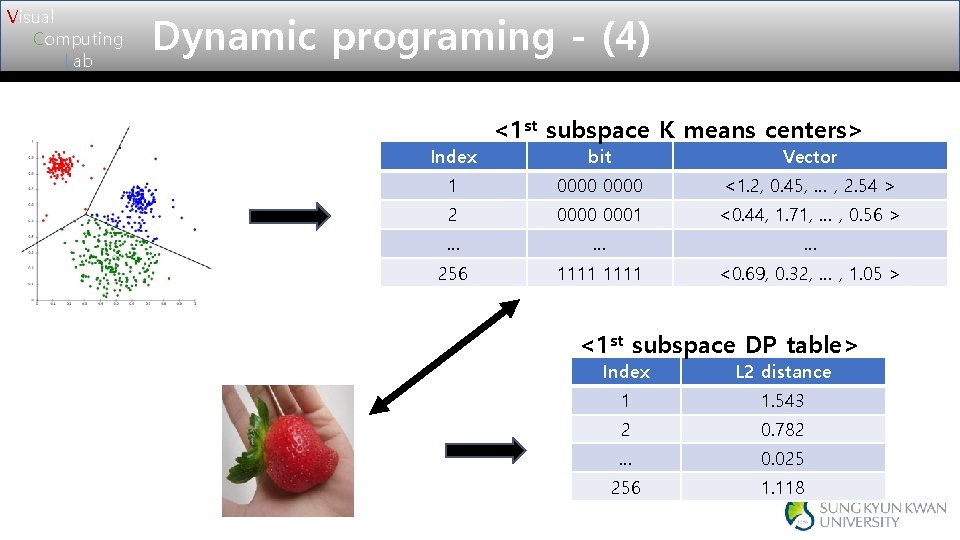
Visual Computing Lab Dynamic programing - (4) Index <1 st subspace K means centers> bit Vector 1 0000 <1. 2, 0. 45, … , 2. 54 > 2 0000 0001 <0. 44, 1. 71, … , 0. 56 > … … … 256 1111 <0. 69, 0. 32, … , 1. 05 > <1 st subspace DP table> Index L 2 distance 1 1. 543 2 0. 782 … 0. 025 256 1. 118

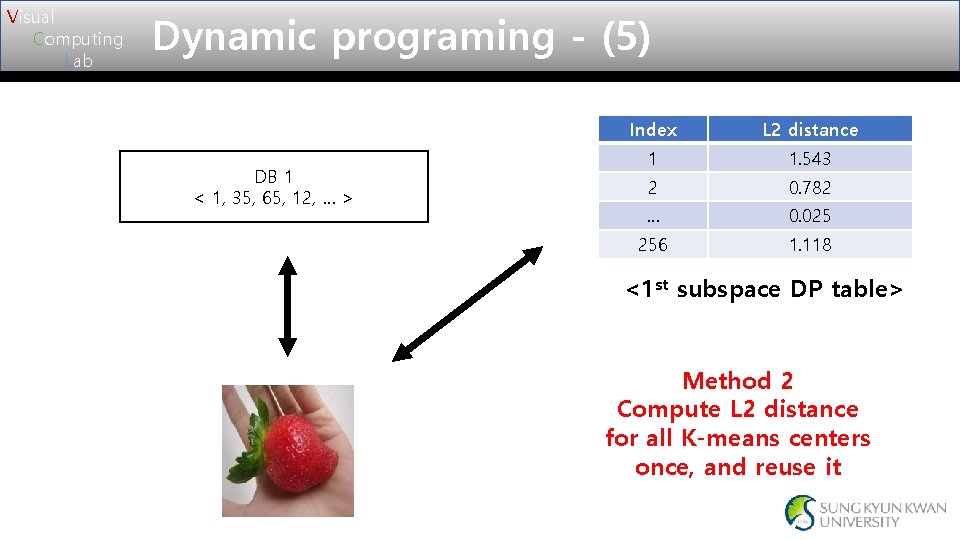
Visual Computing Lab Dynamic programing - (5) DB 1 < 1, 35, 65, 12, … > Index L 2 distance 1 1. 543 2 0. 782 … 0. 025 256 1. 118 <1 st subspace DP table> Method 2 Compute L 2 distance for all K-means centers once, and reuse it

Visual Computing Lab Qn. A