Viso Computacional Geometria de Transformaes F Luiz M

Visão Computacional Geometria de Transformações F Luiz M. G. Gonçalves www. dca. ufrn. br/~lmarcos/courses/visao

Transformações FVetores, bases e matrizes FTranslação, rotação e escala FCoordenadas homogêneas FRotações e translações 3 D

Vetor FEntidade Física w Exemplos: FEntidade Geométrica w Exemplos:

Vetores FNoção da Física: w comprimento, direção, sentido FExemplos: w velocidade, força, deslocamento FRepresentação matemática: w Enuplas ordenadas v = (v 1, v 2, …, vn) u v

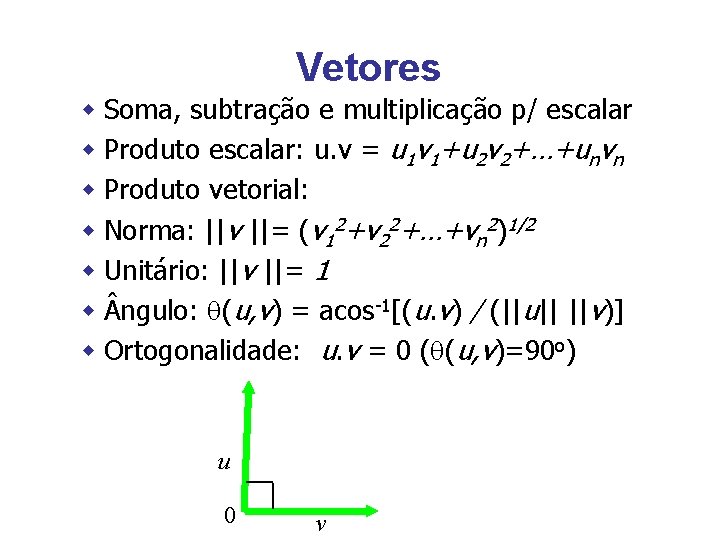
Vetores w Soma, subtração e multiplicação p/ escalar w Produto escalar: u. v = u 1 v 1+u 2 v 2+…+unvn w Produto vetorial: w Norma: ||v ||= (v 12+v 22+…+vn 2)1/2 w Unitário: ||v ||= 1 w ngulo: (u, v) = acos-1[(u. v) / (||u|| ||v)] w Ortogonalidade: u. v = 0 ( (u, v)=90 o) u 0 v

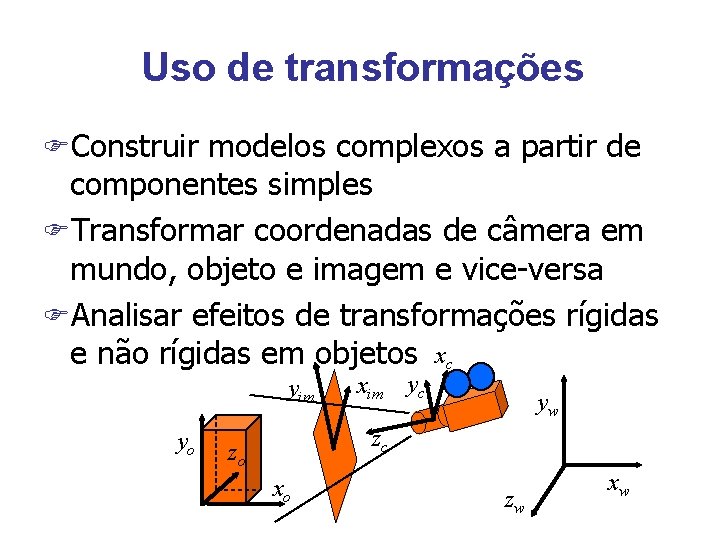
Uso de transformações FConstruir modelos complexos a partir de componentes simples FTransformar coordenadas de câmera em mundo, objeto e imagem e vice-versa FAnalisar efeitos de transformações rígidas e não rígidas em objetos xc yim yo xim yc yw zc zo xo zw xw

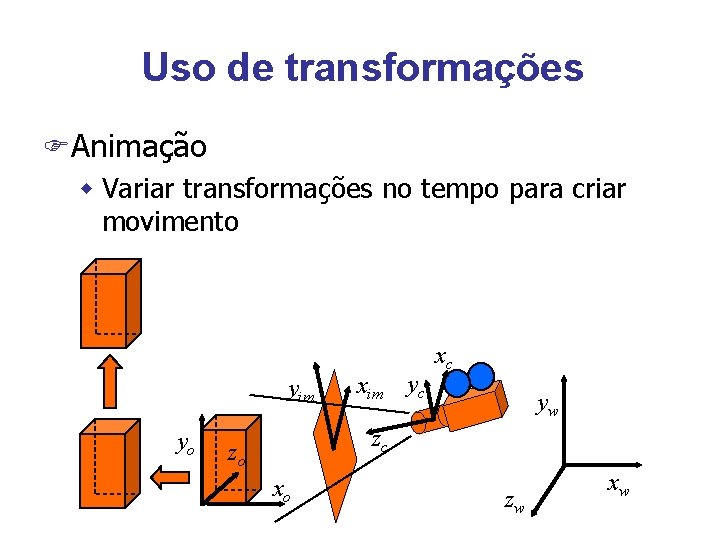
Uso de transformações FAnimação w Variar transformações no tempo para criar movimento yim yo xim yc xc yw zc zo xo zw xw

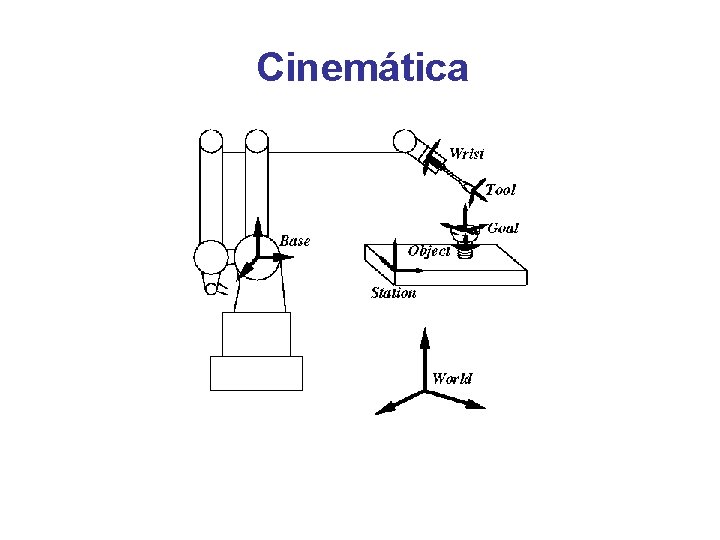
Cinemática

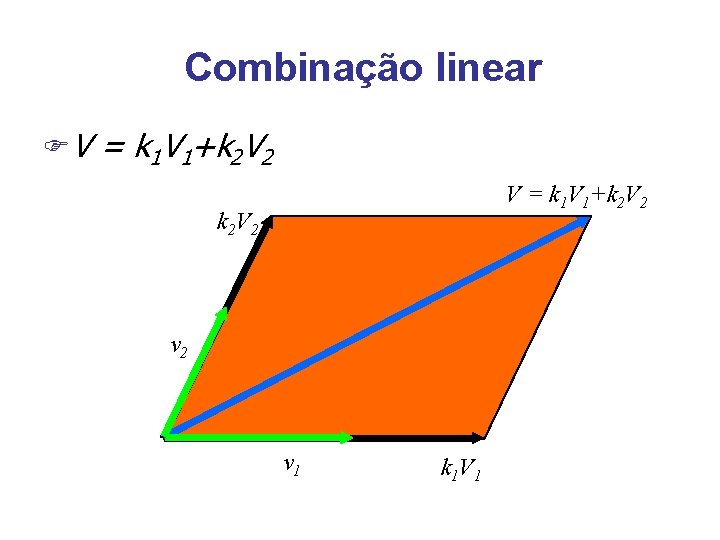
Combinação linear F Dados dois vetores v 1 e v 2, ande uma distância qualquer na direção de v 1 e então ande outra distância na direção de v 2 F O conjunto de todos os lugares (vetores, pontos) que podem ser atingidos é dado pelas combinações lineares possíveis entre v 1 e v 2 F Um conjunto de vetores é dito linearmente independentes se nenhum deles pode ser escrito como uma combinação linear dos outros

Combinação linear FV = k 1 V 1+k 2 V 2 v 1 k 1 V 1

Independência Linear FUm conjunto de vetores é dito linearmente independente se nenhum dos vetores pode ser escrito como uma combinação linear dos outros FExemplo de 3 vetores LI: w e 1 = (1, 0, 0) w e 2 = (0, 1, 0) w e 3 = (0, 0, 1)

Bases vetoriais F Uma base vetorial é um conjunto de vetores linearmente independentes entre si, cuja combinação linear leva a qualquer lugar dentro do espaço, isto é, varre o espaço. F Para varrer um espaço n-dimensional, são necessários n vetores F Se a base é normalizada e os vetores mutuamente ortogonais, ela é dita ser ortonormal F Obviamente, há muito mais que uma base possível para um dado espaço vetorial.

Representação de vetores F Todo vetor tem uma representação única numa dada base w Os multiplicadores pelos vetores da base são chamados de componentes ou coordenadas w Mudando a base, muda os componentes, mas não o vetor V= v 1 E 1+v 2 E 2+. . . +vn. En F Os vetores E 1, E 2, . . . , En são a base F Os escalares v 1, v 2 , . . . , vn são os componentes de v com respeito à base.

Transformação Linear e Afim FUma função (ou mapeamento ou ainda transformação) F é linear se, para todos os vetores v 1 e v 2 e todos escalares k: F(V 1+V 2) = F(V 1) + F(V 2) F(k. V 1) = k. F(V 1) FQualquer mapeamento linear é completamente especificado pelo seu efeito numa base vetorial

Efeito na base v = v 1 E 1+ v 2 E 2+ v 3 E 3 F(v) = F(v 1 E 1+v 2 E 2+v 3 E 3)= = F(v 1 E 1)+F(v 2 E 2)+F(v 3 E 3)= = v 1 F(E 1) + v 2 F(E 2)+v 3 F(E 3) FUma função F é afim se ela é linear mais uma translação w Então a função y = m. X+b não é linear, mas é afim

Transformando um vetor (f 11 v 1+f 12 v 2 +f 13 v 3)E 1+(f 21 v 1+f 22 v 2+f 23 v 3)E 2+(f 31 v 1+f 32 v 2+f 33 v 3)E 3 FAs coordenadas do vetor da base transformado (em termos dos vetores da base original): F(E 1) = f 11 E 1 +f 21 E 2+f 31 E 3 F(E 2) = f 12 E 1 +f 22 E 2+f 32 E 3 F(E 3) = f 13 E 1 +f 23 E 2+f 33 E 3 FO vetor geral V transformado torna-se: F(V) = v 1 F(E 1) + v 2 F(E 2)+v 3 F(E 3) = v 1(f 11 E 1+f 21 E 2+f 31 E 3)+v 2(f 12 E 1+f 22 E 2+f 32 E 3)+v 3(f 13 E 1+f 23 E 2+f 33 E 3)= (f 11 v 1+f 12 v 2 +f 13 v 3)E 1+(f 21 v 1+f 22 v 2+f 23 v 3)E 2+(f 31 v 1+f 32 v 2+f 33 v 3)E 3

Transformando um vetor FSuas coordenadas ainda em referência a E tornam-se: v 1´= f 11 v 1 +f 12 v 2+f 13 v 3 v 2´= f 21 v 1+f 22 v 2+f 23 v 3 v 3´= f 31 v 1+f 32 v 2+f 33 v 3 FOu simplesmente vi = fijvj que é a fórmula de multiplicação matricial

Multiplicação de matrizes! FUma matriz F de dimensões nxn representa uma função linear em n dimensões w A i-ésima coluna mostra o que a função faz ao vetor de base correspondente FTransformação é uma combinação linear das colunas de F w Primeiro componente do vetor de entrada escala a primeira coluna da matriz w acumula no vetor de saída w repete para cada coluna e componente

Exemplo: ACHANDO A MATRIZ FF: R 2 ->R 2: (x, y) -> (2 x, 3 y) FE 1 = (1, 0), E 2 = (0, 1) FF(E 1) = (2, 0) FF(E 2) =(0, 3) FEm forma matricial: 2 0 X F 03 Y FF: R 2 ->R 2: (x, y) -> (2 x+y, 3 y+x)

Multiplicação matricial FUsualmente calcula-se de modo diferente w faça o produto interno da coluna i da matriz com o vetor de entrada para conseguir componente i do vetor de saída: v 1 ´ f 11 f 12 f 13 v 2´ = f 21 f 22 f 23 v 3 ´ f 31 f 32 f 33 v 1 v 2 v 3

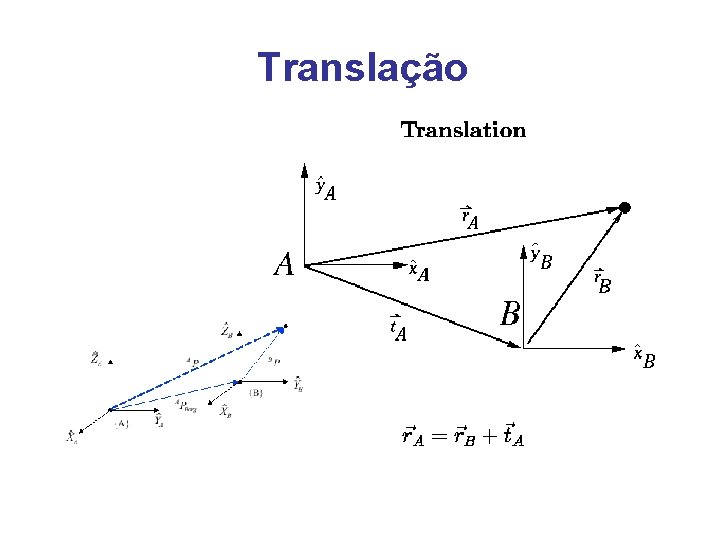
Translação

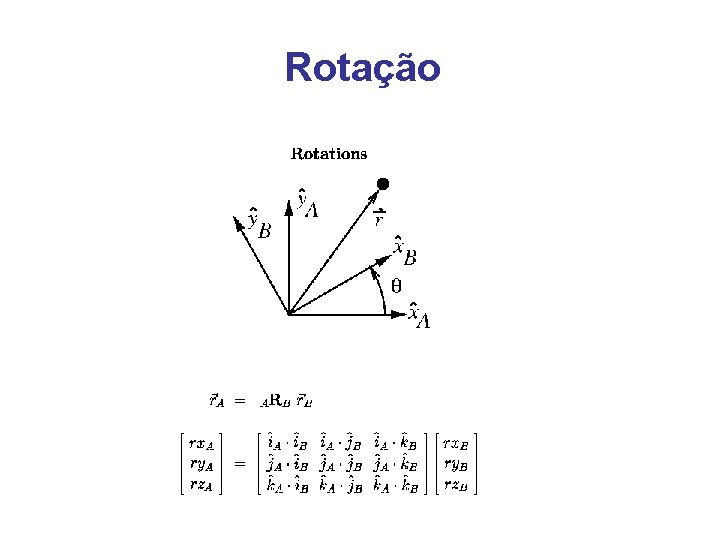
Rotação

Matriz de rotação possui vetores unitários

Representação da rotação

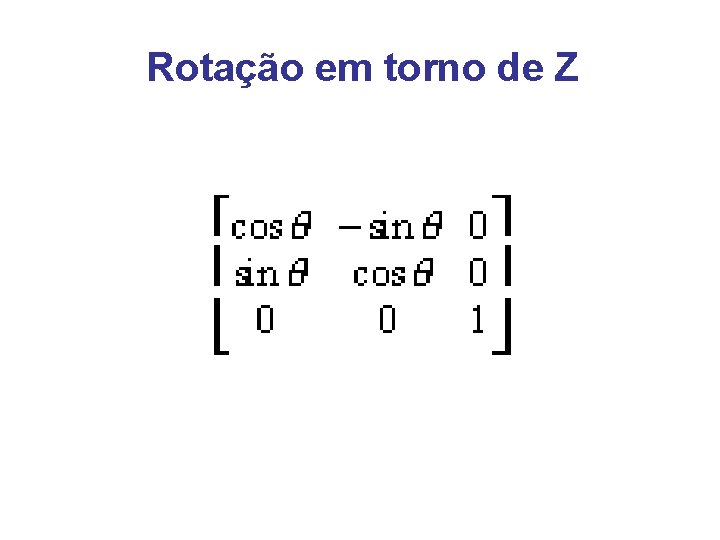
Rotação em torno de Z

Exemplo de rotação

Relações espaciais F Representação em relação a um frame (sistema de coordenadas) F P (X, Y, Z)

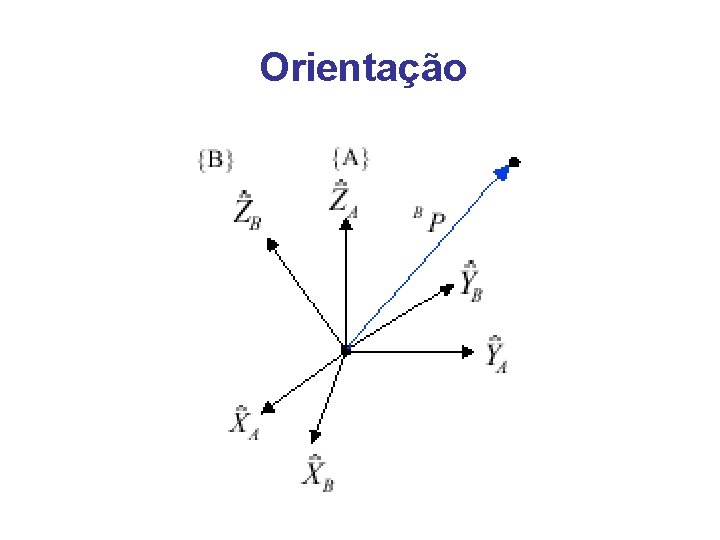
Orientação

Orientação

Matriz de orientação

Propriedade elementar (unitária)

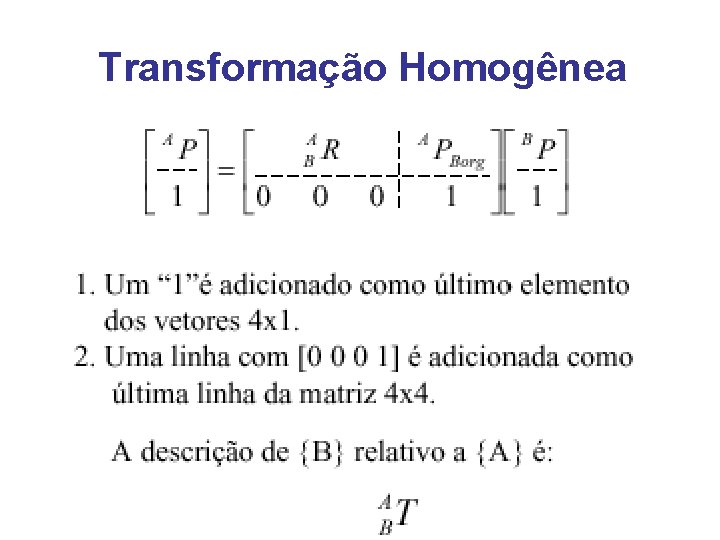
Transformações Homogêneas FJuntando posição e orientação

Juntando orientação e posição

Coordenadas Homogêneas

Juntar rotação e translação

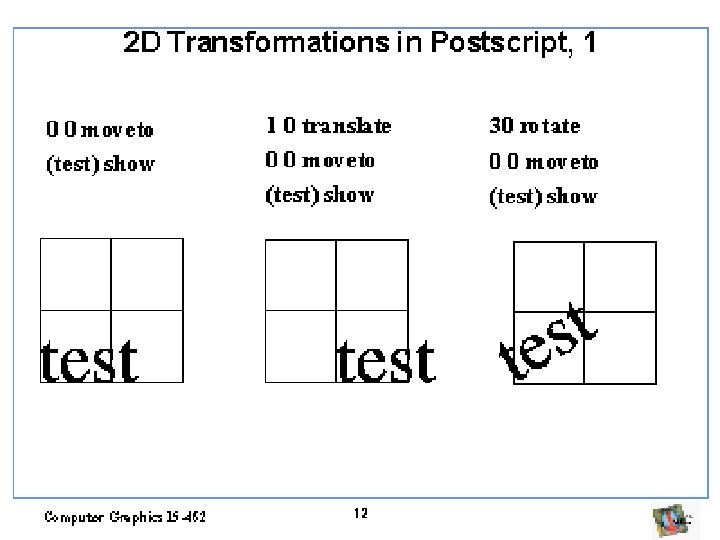
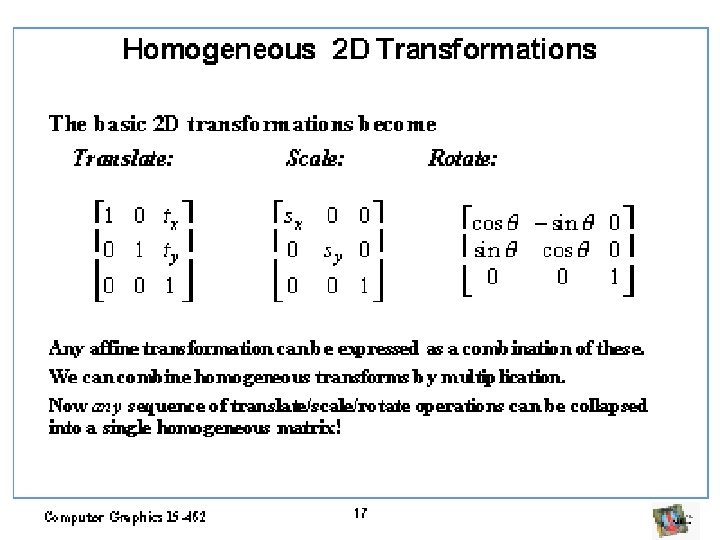
Coordenadas homogêneas FTranslação não é linear. Como representar em forma de matriz? w Adiciona uma coordenada extra a cada vetor x´ y´ z´ 1 = 1 0 0 0 0 1 0 FCoordenada extra é chamada de tx ty tz 1 x y z 1 homogênea (ou w) FTransformação denominada homogênea

Transformação Homogênea

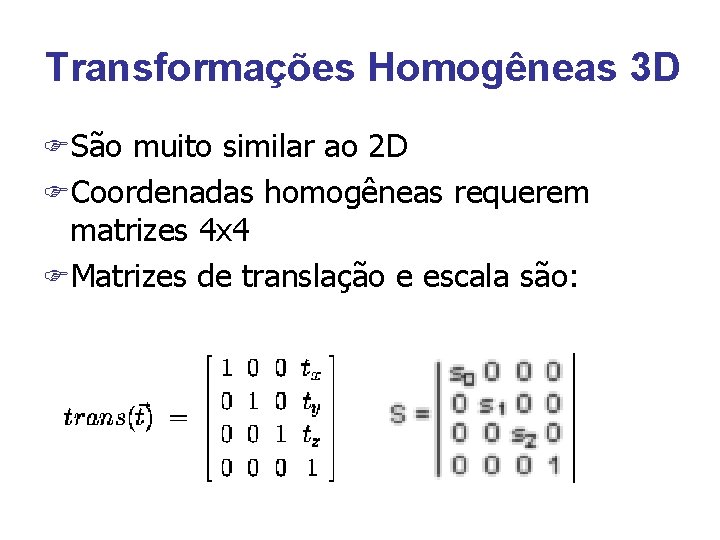
Transformações Homogêneas 3 D FSão muito similar ao 2 D FCoordenadas homogêneas requerem matrizes 4 x 4 FMatrizes de translação e escala são:

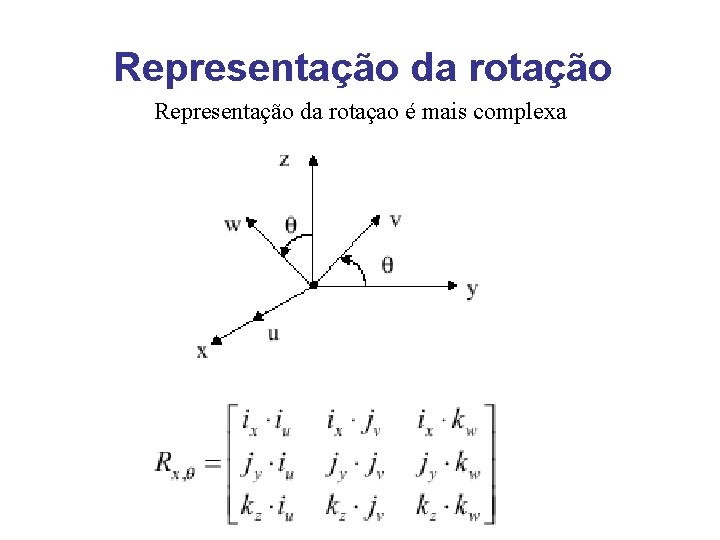
Representação da rotação Representação da rotaçao é mais complexa

Rotação 3 D FRotação é um pouco mais complicado FSistema de coordenadas de mão direita ou esquerda afeta direção de rotação FSistema de mão direita y x z FSistema de mão esquerda y z x

Produto Cruzado (Vetorial) F Eixo Z é determinado a partir dos eixos X e Y pelo produto vetorial F Produto vetorial segue regra da mão direita em um sistema de mão direita e regra da mão esquerda em um sistema de mão esquerda F Estaremos trabalhando quase sempre com sistema de mão direita

Matriz dual F Se v = (x, y, z) é um vetor, a matriz v*= é denominada matriz dual de v F Produto vetorial: v x a = v* a w Ajuda a definir rotações em torno de eixo arbitrário w Velociade angular e matriz dual vezes derivadas F Interpretação geométrica de v* a: w Projeta a num plano normal a v w Rotaciona de 90º em torno de v w Vetor resultante é perpendicular a v e a a

ngulos de Euler para rotações 3 D F ngulos de Euler: 3 rotações em torno de cada eixo, porém: w Interpolação de ângulos para animação produz movimentos bizarros w Rotações dependem da ordem, e não existem convenções para que ordem usar FUsado amplamente, devido à simplicidade FConhecidos como row, pitch, yaw

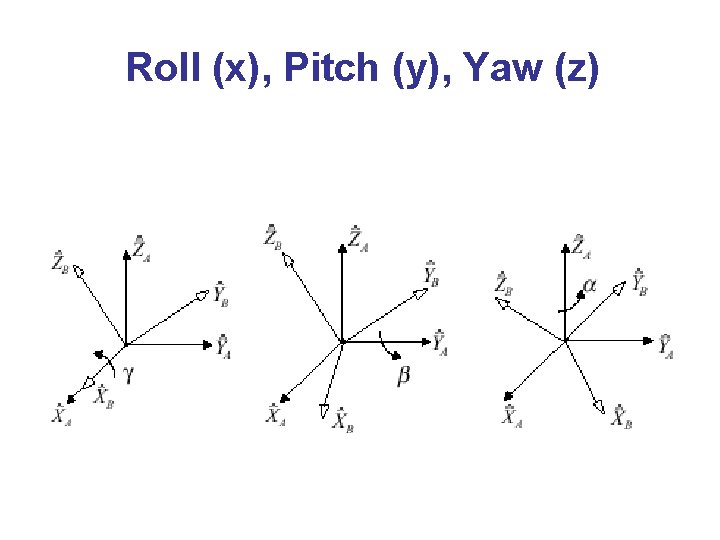
Roll (x), Pitch (y), Yaw (z)

Rotação em torno de cada eixo

Generalização da Rotação

Rotação arbitrária F Dado um eixo ou direção (x, y, z) e um ângulo , a matriz de rotação fica: - (Px, Py, Pz) Y (Px’, Py’, Pz’) (x, y, z) X Z

Exemplo de rotação + translação

Exemplo: continuação

Problema da comutatividade F Translação seguida de rotação é diferente de rotação seguida de translação

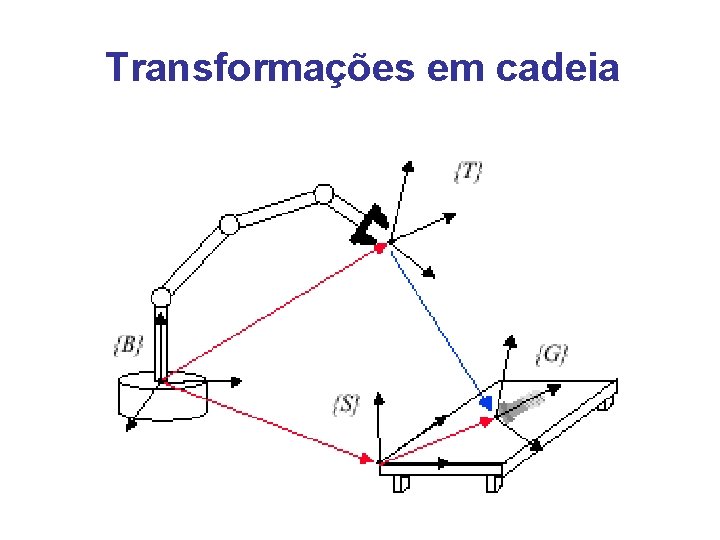
Transformações em cadeia

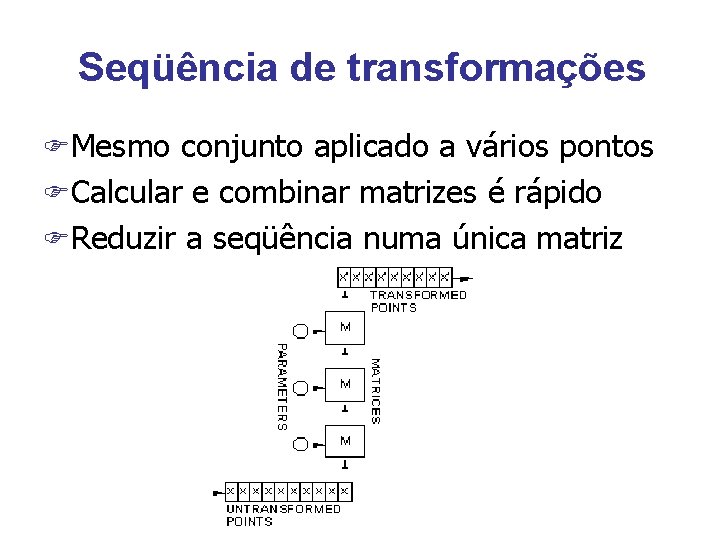
Seqüência de transformações FMesmo conjunto aplicado a vários pontos FCalcular e combinar matrizes é rápido FReduzir a seqüência numa única matriz

Colapsando transformações FConsidere a seqüência p’=ABCDp FMultiplicação não é comutativa (ordem) FMultiplicação é associativa w Da esquerda para a direita (pré-multiplicação) w Direita para a esquerda (pós-multiplicação) FABCD = (((AB)C)D) = (A(B(CD))) FTroque cada matriz pelo produto do par

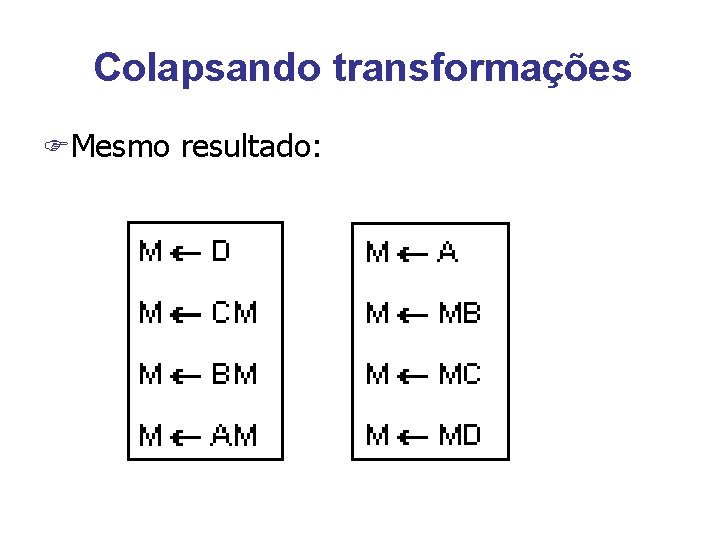
Colapsando transformações FMesmo resultado:

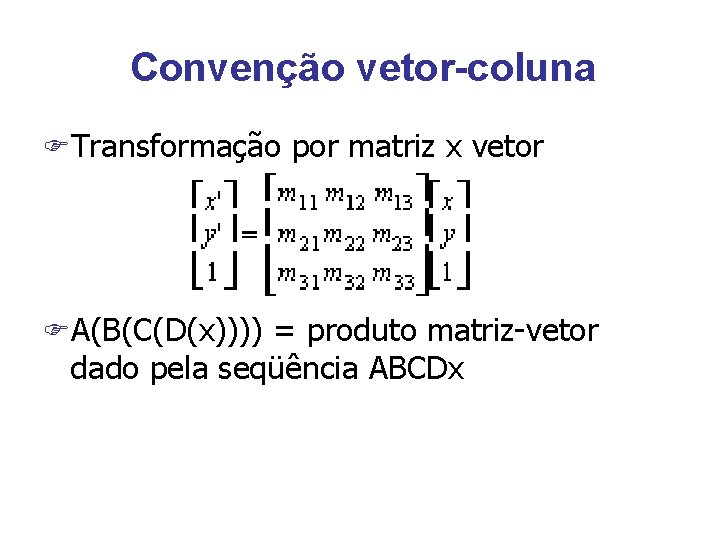
Convenção vetor-coluna FTransformação por matriz x vetor FA(B(C(D(x)))) = produto matriz-vetor dado pela seqüência ABCDx

Convenção vetor-linha FTransformação por vetor x matriz FTodas as matrizes devem ser transpostas FSeqüência ABCDx transposta é xt. Dt. Ct. Bt. At FOpen. GL usa esta regra

Invertendo a transf. homogênea