Visiblity Culling and Clipping Computer Graphics COMP 770

Visiblity: Culling and Clipping Computer Graphics COMP 770 (236) Spring 2009 January 21 & 26: 2009 1

Today’s topics ■ Lines and planes ■ Culling ° ° View frustum culling Back-face culling Occlusion culling Hierarchical culling ■ Clipping 2

What are culling and clipping? ■ Culling ° Throws away entire objects and primitives that cannot possibly be visible ° An important rendering optimization (esp. for large models) ■ Clipping ° “Clips off” the visible portion of a primitive ° Simplifies rasterization ° Used to create “cut-away” views of a model 3

Culling example ■ Power plant model ° 13 M triangles ° 1. 7 M triangles - gutted version show here with no internal pipes 4

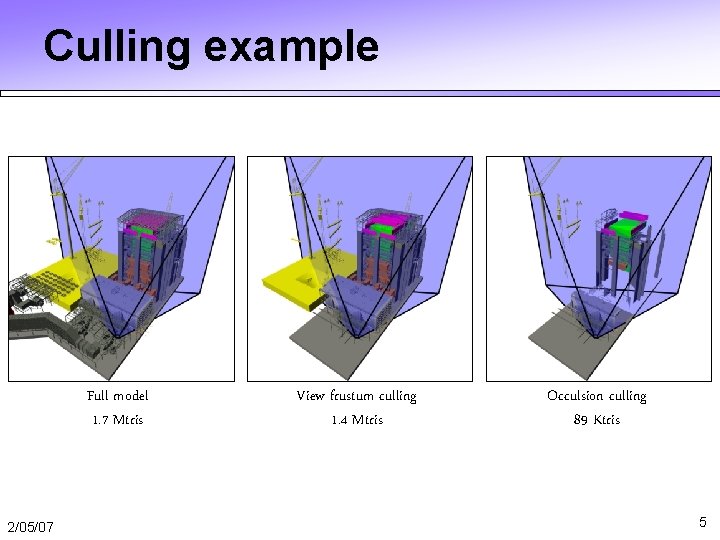
Culling example Full model 1. 7 Mtris 2/05/07 View frustum culling 1. 4 Mtris Occulsion culling 89 Ktris 5

Lines and planes ■ Implicit equation for line (plane): l 0 = p d (0, 0) ■ If is normalized then d gives the distance of the line (plane) from the origin along ■ Transforming points and lines with transformation M: points: lines: 6

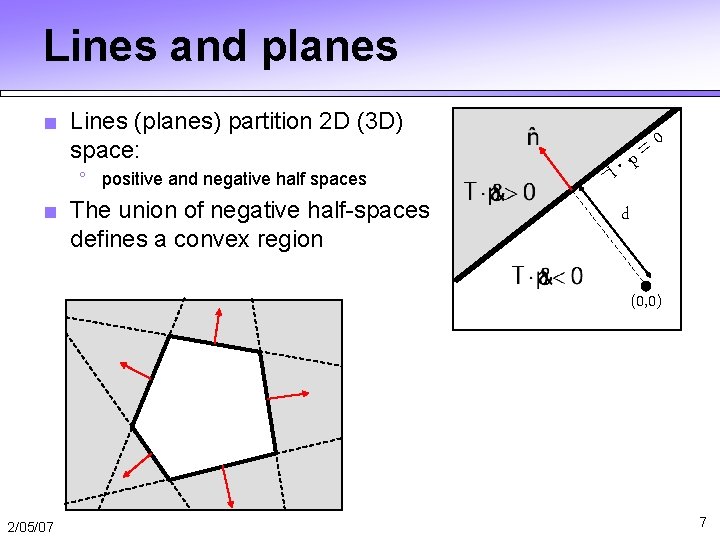
Lines and planes ■ Lines (planes) partition 2 D (3 D) space: ° positive and negative half spaces ■ The union of negative half-spaces defines a convex region l 0 = p d (0, 0) 2/05/07 7

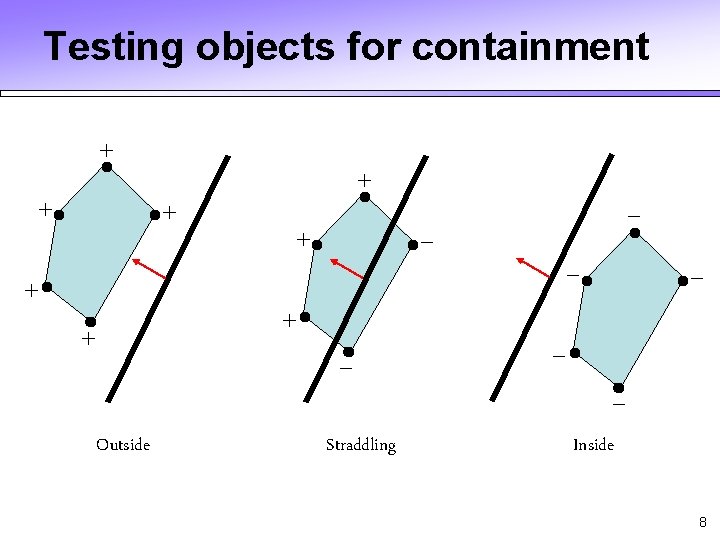
Testing objects for containment + + + - - Outside Straddling Inside 8

Conservative testing r r r Outside Indeterminate Inside ■ Use cheap, conservative bounds for trivial cases ■ Can use more accurate, more expensive tests for ambiguous cases if needed 2/05/07 9

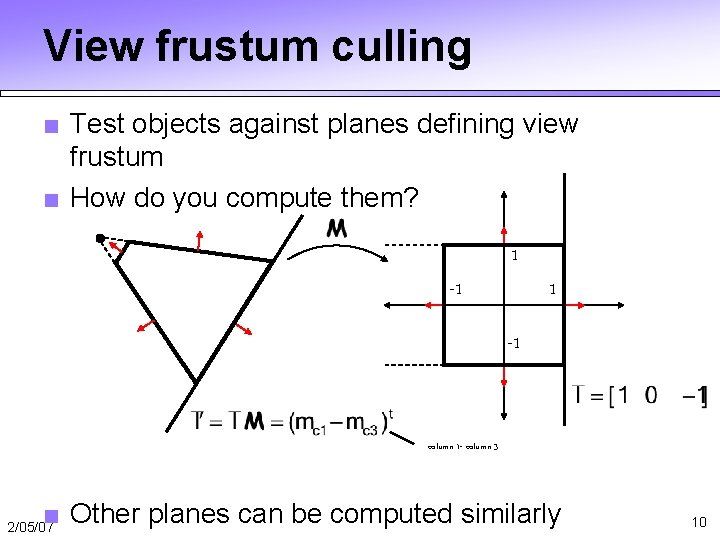
View frustum culling ■ Test objects against planes defining view frustum ■ How do you compute them? 1 -1 column 1 - column 3 ■ Other planes can be computed similarly 2/05/07 10

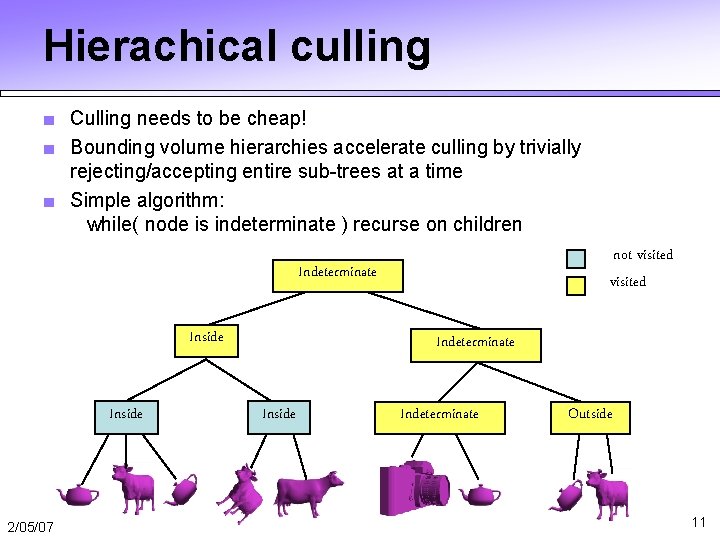
Hierachical culling ■ Culling needs to be cheap! ■ Bounding volume hierarchies accelerate culling by trivially rejecting/accepting entire sub-trees at a time ■ Simple algorithm: while( node is indeterminate ) recurse on children not visited Indeterminate Inside 2/05/07 Indeterminate Inside Indeterminate Outside 11

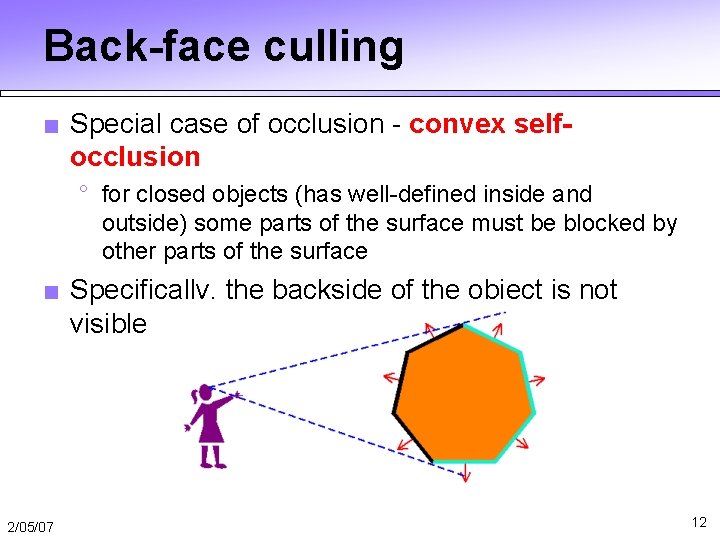
Back-face culling ■ Special case of occlusion - convex selfocclusion ° for closed objects (has well-defined inside and outside) some parts of the surface must be blocked by other parts of the surface ■ Specifically, the backside of the object is not visible 2/05/07 12

Manifold ■ Back-face culling can be applied to any orientable twomanifold. ■ Orientable two-manifolds have the following properties. 1. All points on the surface are locally like a plane. No holes, cracks, or self -intersections. 2. Boundary partitions 3 D space into interior and exterior regions ■ In our case, manifolds will be composite objects made of many primitives, generally triangles. ■ Back-face culling eliminates a subset of these primitives. ° Assumes that you are outside of all objects. 13

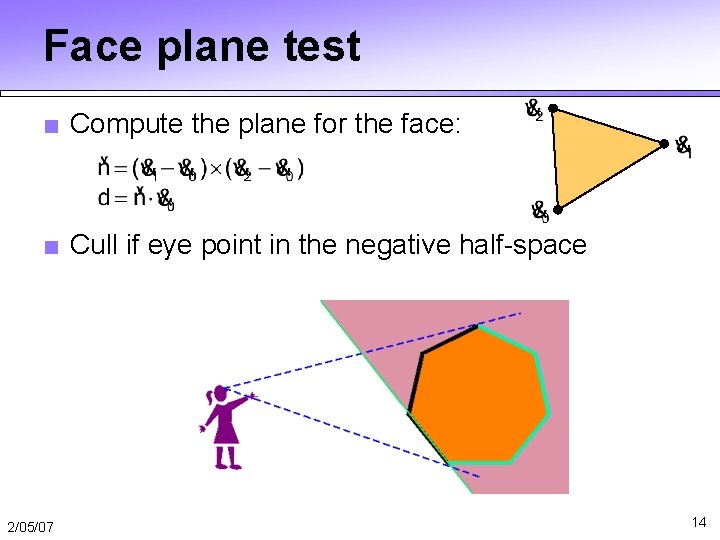
Face plane test ■ Compute the plane for the face: ■ Cull if eye point in the negative half-space 2/05/07 14

Winding order test ■ Back-faces have a clockwise vertex ordering when viewed from outside. ■ Typically used by graphics hardware during triangle setup 15

Back-face culling in Open. GL ■ Can cull front faces or back faces ■ Back-face can sometimes double performance if (cull): gl. Front. Face(GL_CCW) gl. Enable(GL_CULL_FACE) gl. Cull. Face(GL_BACK) else: gl. Disable(GL_CULL_FACE) # define winding order # enable Culling # which faces to cull front-face culling 2/05/07 16

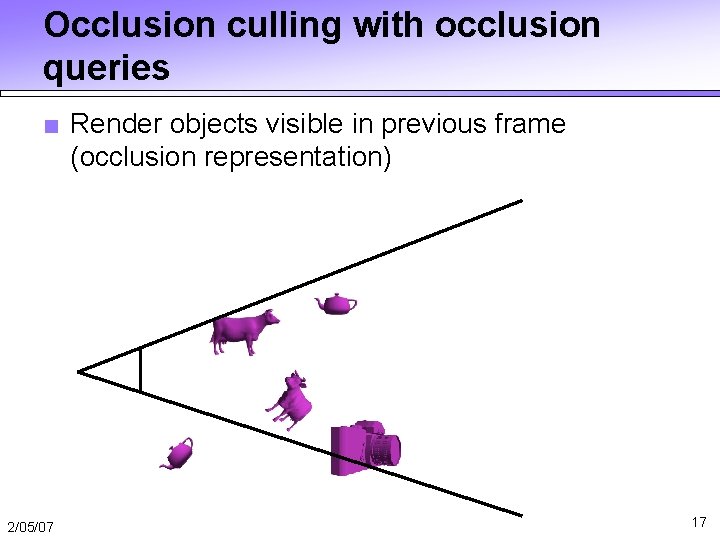
Occlusion culling with occlusion queries ■ Render objects visible in previous frame (occlusion representation) 2/05/07 17

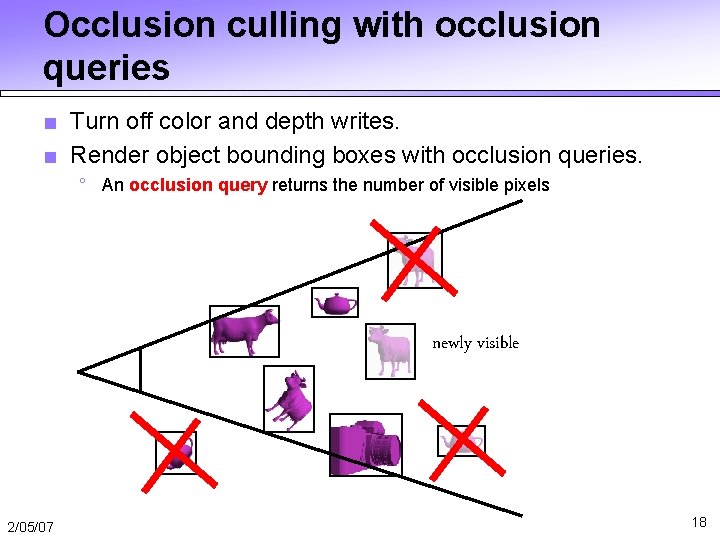
Occlusion culling with occlusion queries ■ Turn off color and depth writes. ■ Render object bounding boxes with occlusion queries. ° An occlusion query returns the number of visible pixels newly visible 2/05/07 18

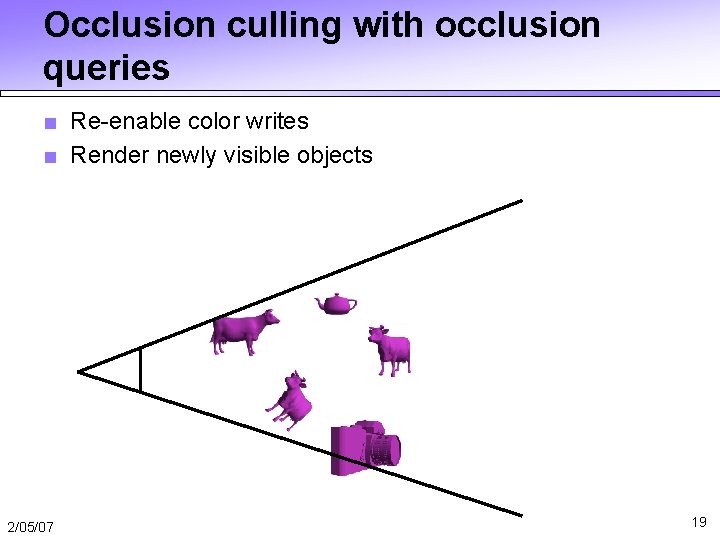
Occlusion culling with occlusion queries ■ Re-enable color writes ■ Render newly visible objects 2/05/07 19

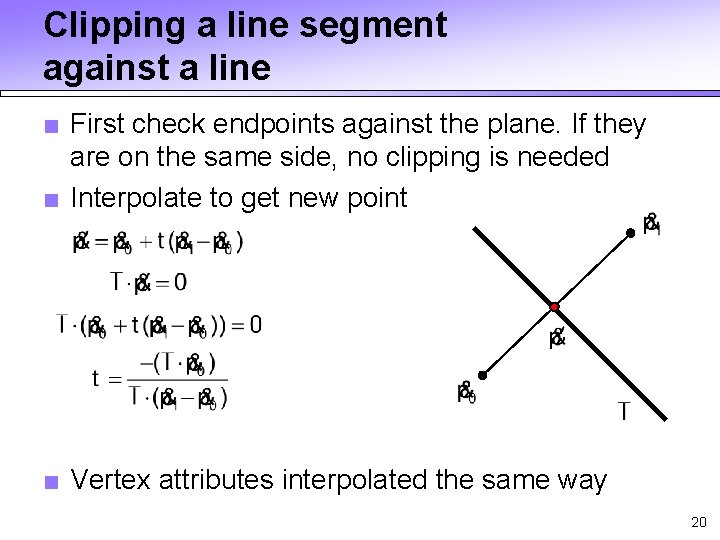
Clipping a line segment against a line ■ First check endpoints against the plane. If they are on the same side, no clipping is needed ■ Interpolate to get new point ■ Vertex attributes interpolated the same way 20

Clipping a polygon against a line ■ ■ ■ Traverse edges Keep edges that are entirely inside Create new point when we exit Throw away edges entirely outside Create new point and new edge when we enter 21

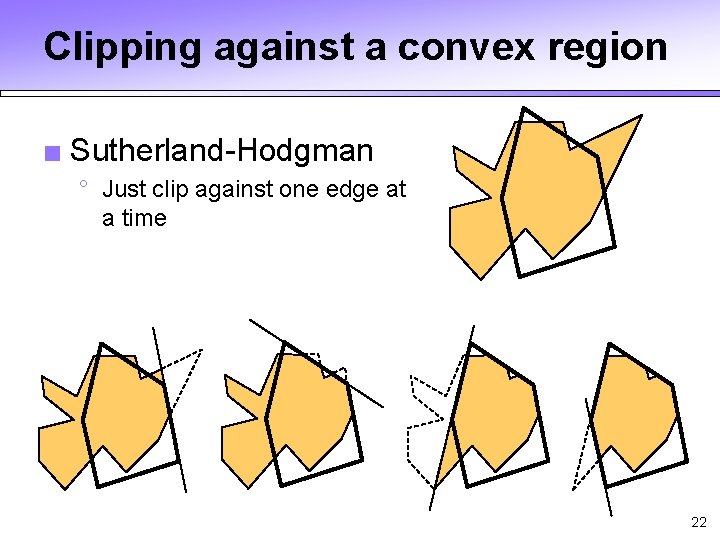
Clipping against a convex region ■ Sutherland-Hodgman ° Just clip against one edge at a time 22

Homogeneous clipping ■ NDC simplify view frustum clipping ■ Clip after applying projection matrix, but before the divide by w Add extra coordinate so we can use our line equation ° clip coordinates w -1 1 x ■ Easy in/out test and interpolation. Other coordinates treated exactly the same way 2/05/07 23

Culling and clipping in the rendering pipeline Culling done by application Eye coordinates. View frustum clipping and back-face culling can be done here View frustum clipping on clip coordinates. Back-face culling done in setup phase of rasterization. 2/05/07 24