Visibility Graphs and Cell Decomposition By David Johnson

Visibility Graphs and Cell Decomposition By David Johnson

Shakey the Robot • Built at SRI • Late 1960’s • For robotics, the equivalent of Xerox PARC’s Alto computer – Alto – mouse, GUI, network, laser printer, WYSIWYG, multiplayer computer game – Shakey – mobile, wireless, path -planning, Hough transform, camera vision, English commands, logical reasoning

Shakey video

Shakey path planning • Represent the world as a hierarchical grid – – Full Partially-full Empty Unknown • Compute nodes at corners of objects • Find shortest path through nodes – A*

Shakey used two good ideas • A* • Putting sub-goals on corners of vertices – This has been generalized into the idea of visibility graphs.

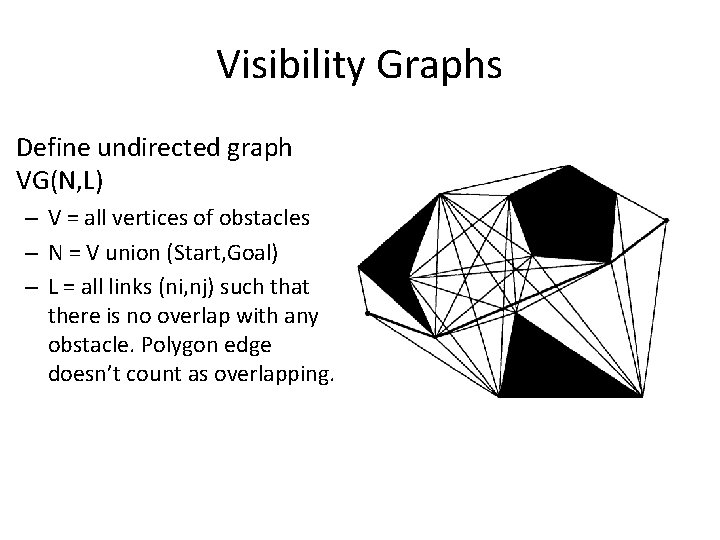
Visibility Graphs Define undirected graph VG(N, L) – V = all vertices of obstacles – N = V union (Start, Goal) – L = all links (ni, nj) such that there is no overlap with any obstacle. Polygon edge doesn’t count as overlapping.

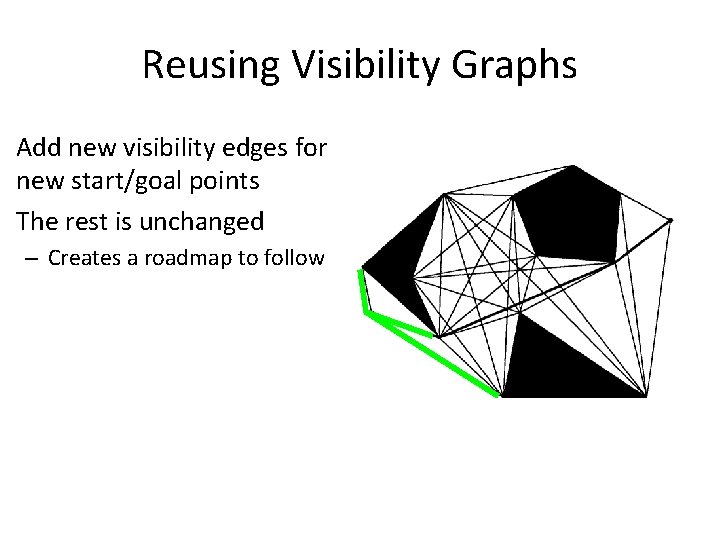
Reusing Visibility Graphs Add new visibility edges for new start/goal points The rest is unchanged – Creates a roadmap to follow

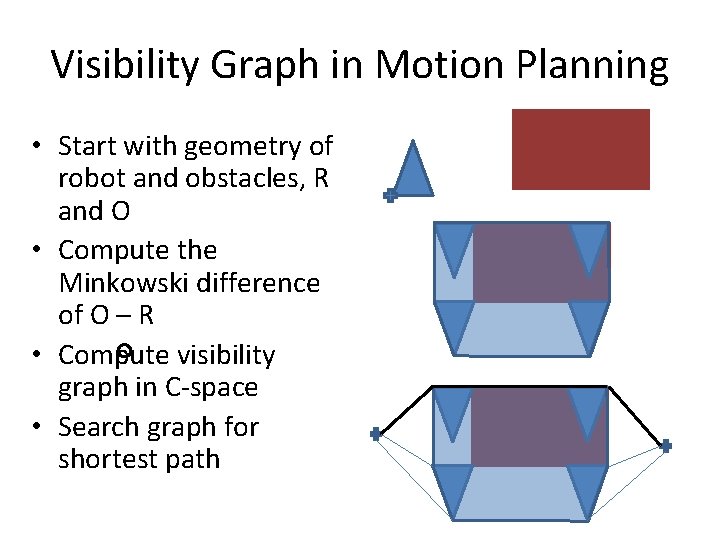
Visibility Graph in Motion Planning • Start with geometry of robot and obstacles, R and O • Compute the Minkowski difference of O – R • Compute visibility graph in C-space • Search graph for shortest path

Computing the Visibility Graph • Brute force • Check every possible edge against all polygon edges

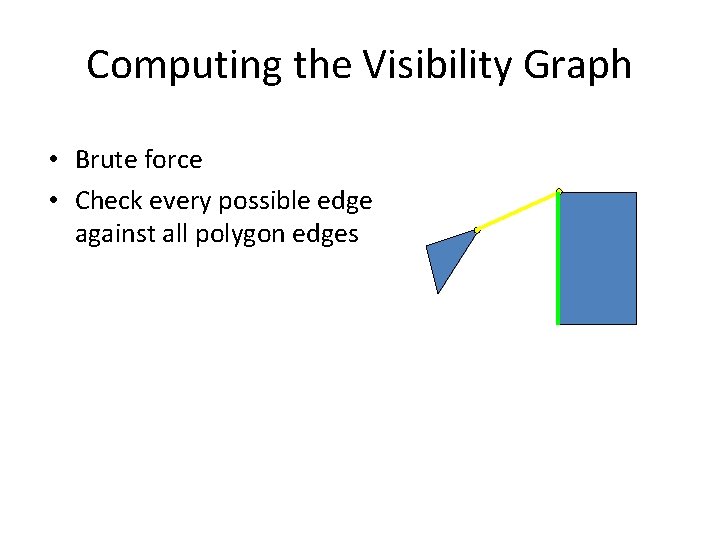
Computing the Visibility Graph • Brute force • Check every possible edge against all polygon edges

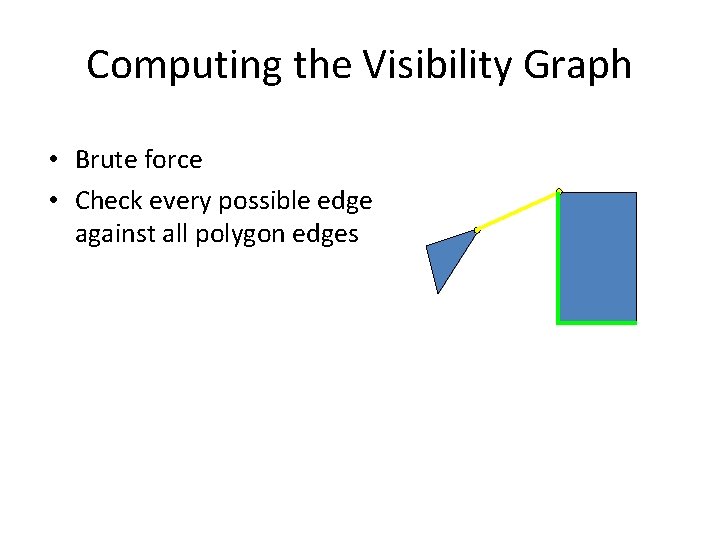
Computing the Visibility Graph • Brute force • Check every possible edge against all polygon edges

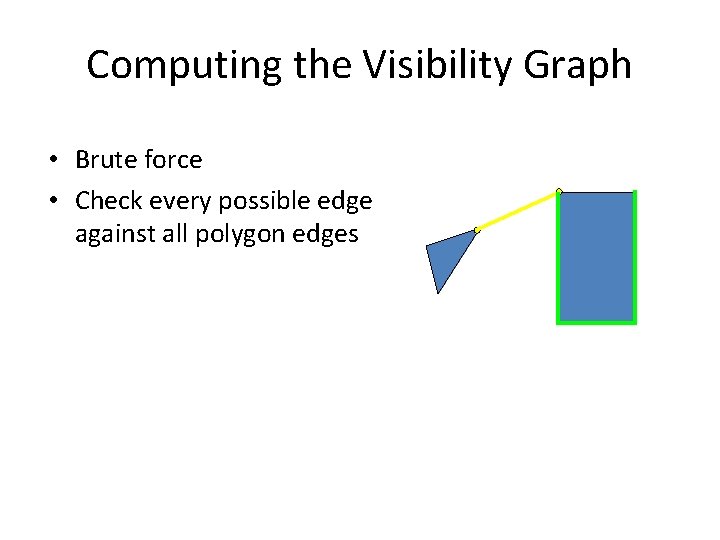
Computing the Visibility Graph • Brute force • Check every possible edge against all polygon edges

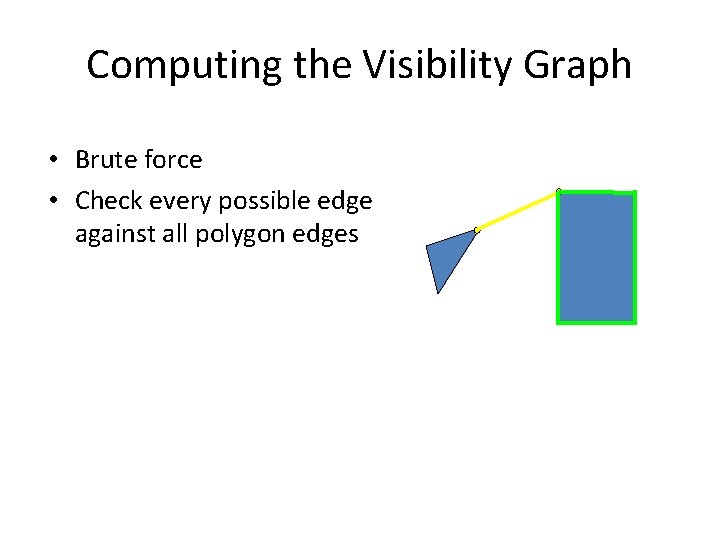
Computing the Visibility Graph • Brute force • Check every possible edge against all polygon edges

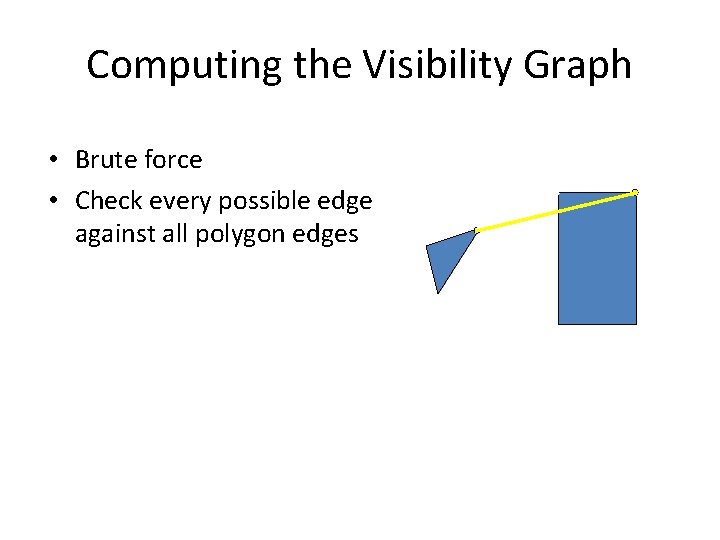
Computing the Visibility Graph • Brute force • Check every possible edge against all polygon edges

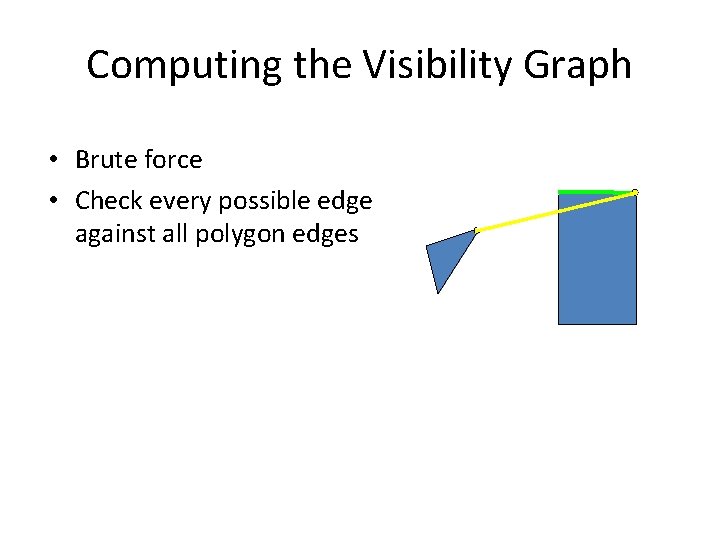
Computing the Visibility Graph • Brute force • Check every possible edge against all polygon edges

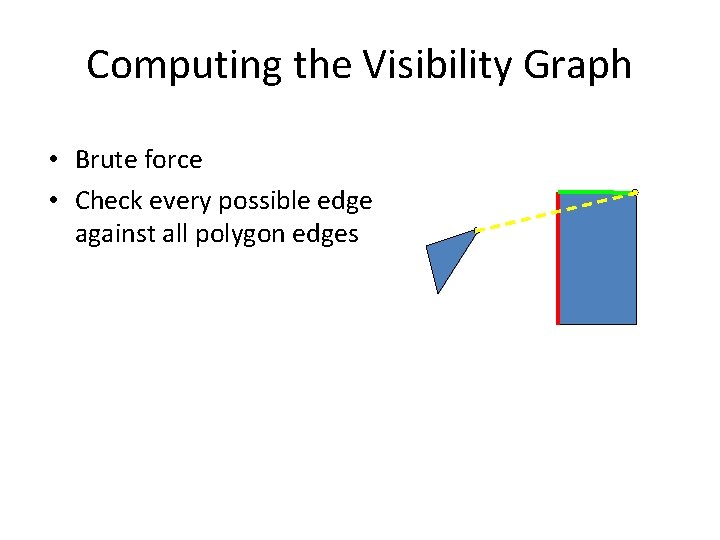
Computing the Visibility Graph • Brute force • Check every possible edge against all polygon edges

Computing the Visibility Graph • Brute force • Check every possible edge against all polygon edges

Special Cases • Do include polygon edges that don’t intersect other polygons • Don’t include edges that cross the interior of any polygon • Minkowski difference of original obstacles may overlap

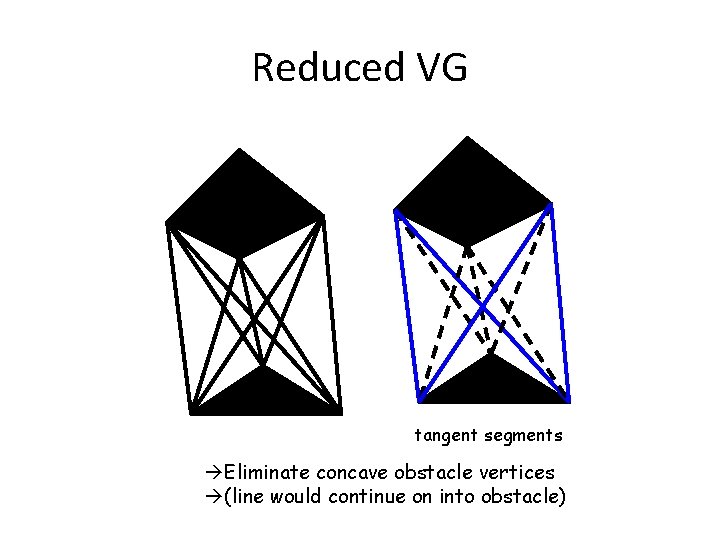
Reduced VG tangent segments àEliminate concave obstacle vertices à(line would continue on into obstacle)

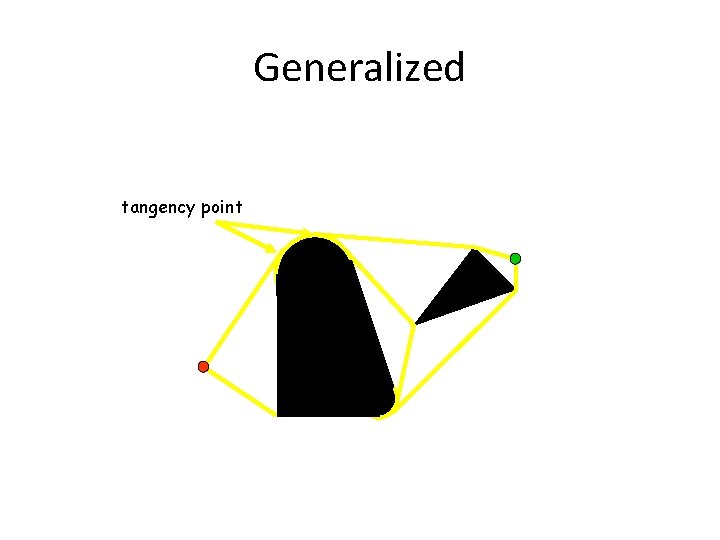
Generalized tangency point

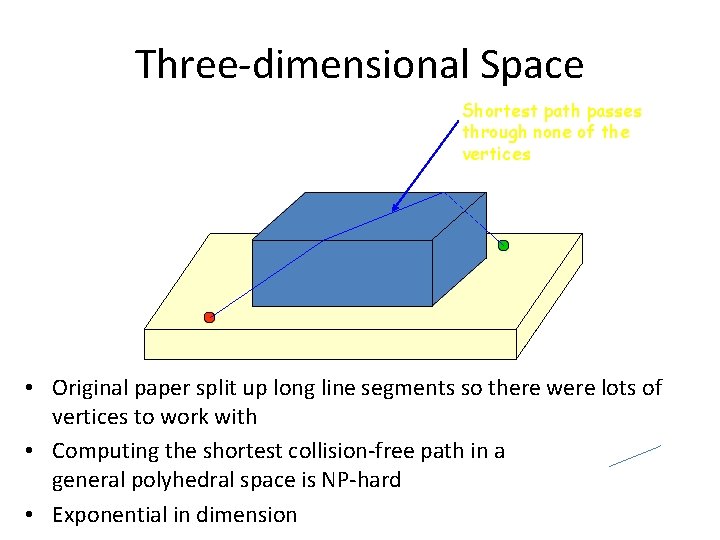
Three-dimensional Space Shortest path passes through none of the vertices • Original paper split up long line segments so there were lots of vertices to work with • Computing the shortest collision-free path in a general polyhedral space is NP-hard • Exponential in dimension

Roadmaps and Coverage • Visibility Graphs make a roadmap through space • Roadmaps not so good for coverage of free space – What kind of robot needs to cover C-free?

Roadmaps and Coverage • Roadmaps not so good for coverage of free space – Vacuum robots – Minesweeper robots – Farming robots • Try to characterize the free space

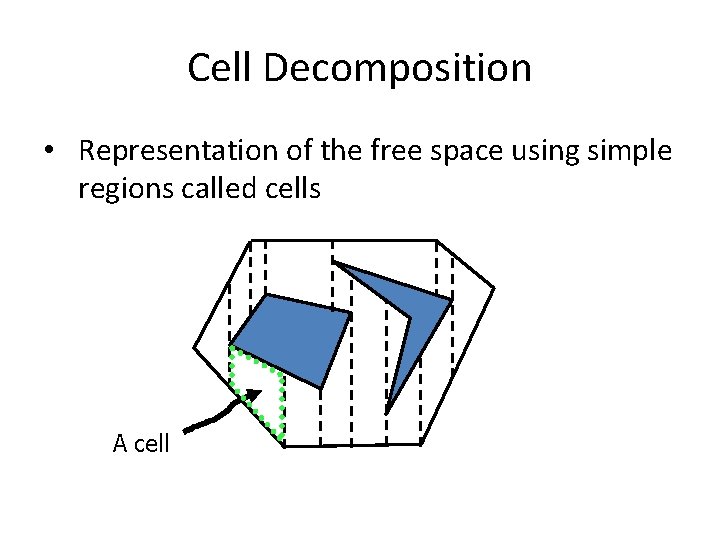
Cell Decomposition • Representation of the free space using simple regions called cells A cell

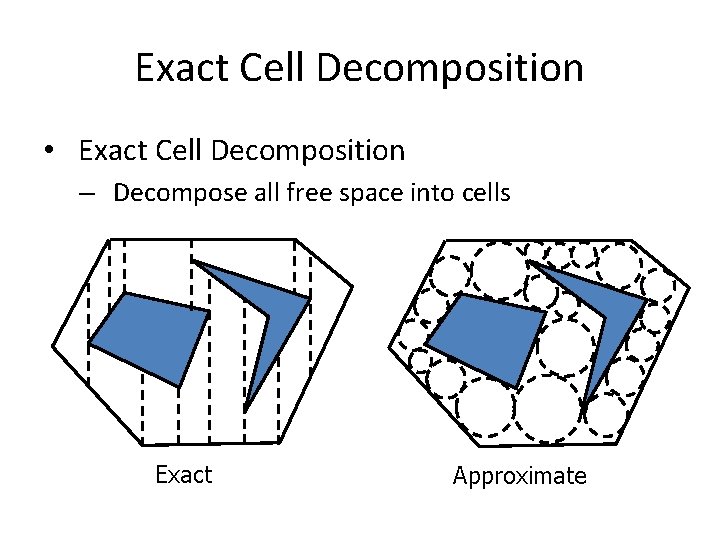
Exact Cell Decomposition • Exact Cell Decomposition – Decompose all free space into cells Exact Approximate

Coverage • Cell decomposition can be used to achieve coverage – Path that passes an end effector over all points in a free space • Cell has simple structure • Cell can be covered with simple motions • Coverage is achieved by walking through the cells

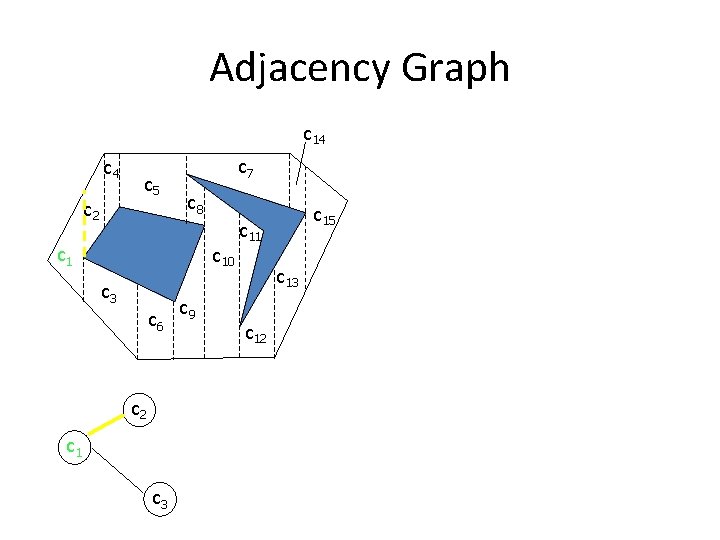
Cell Decomposition • Two cells are adjacent if they share a common boundary • Adjacency graph: – Node correspond to a cell – Edge connects nodes of adjacent cells

Path Planning • Path Planning in two steps: – Planner determines cells that contain the start and goal – Planner searches for a path within adjacency graph

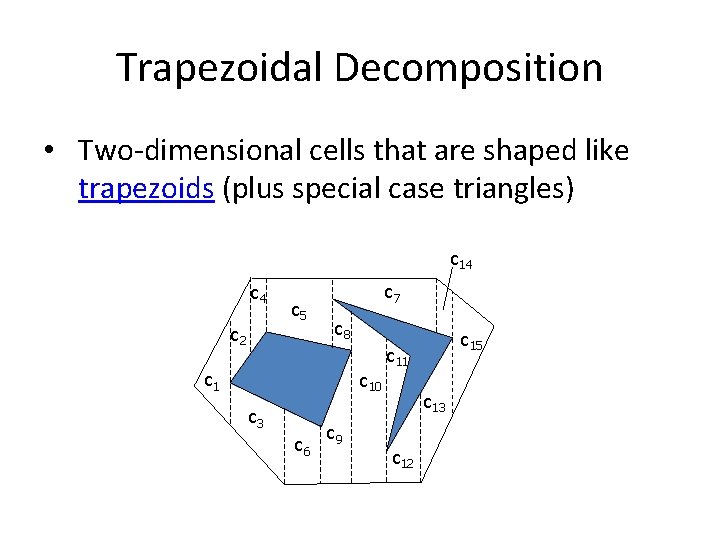
Trapezoidal Decomposition • Two-dimensional cells that are shaped like trapezoids (plus special case triangles) c 14 c 5 c 2 c 7 c 8 c 10 c 3 c 6 c 9 c 15 c 11 c 13 c 12

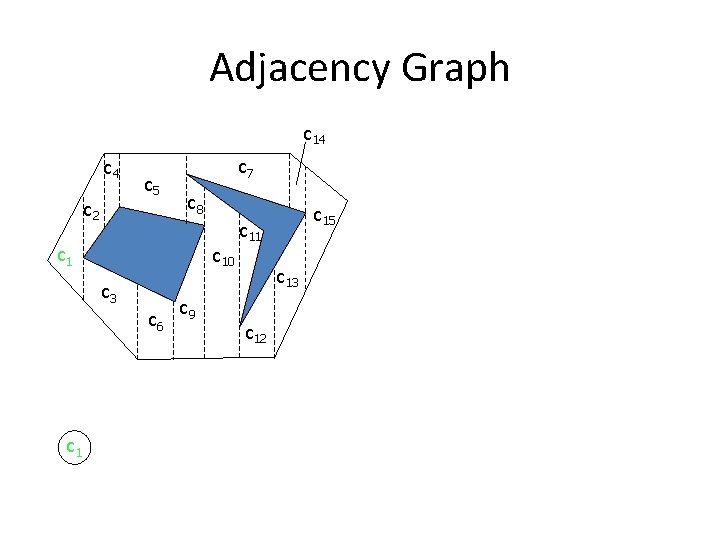
Adjacency Graph c 14 c 5 c 2 c 7 c 8 c 10 c 3 c 6 c 1 c 9 c 15 c 11 c 13 c 12

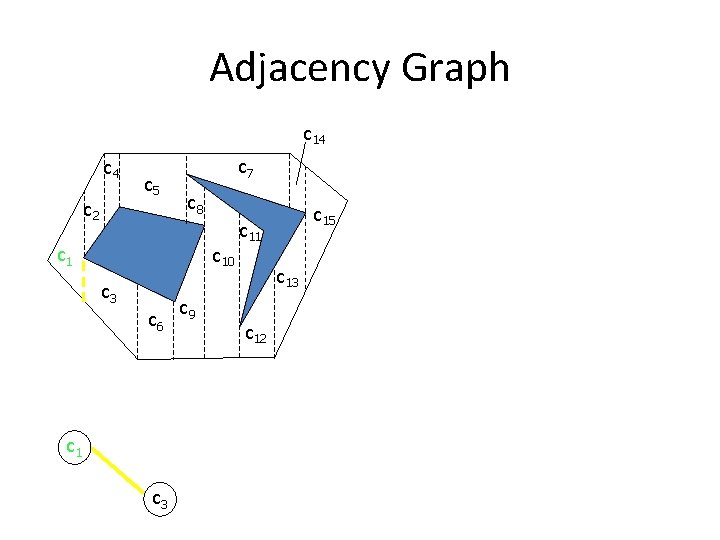
Adjacency Graph c 14 c 5 c 2 c 7 c 8 c 10 c 3 c 6 c 1 c 3 c 9 c 15 c 11 c 13 c 12

Adjacency Graph c 14 c 5 c 2 c 7 c 8 c 10 c 3 c 6 c 2 c 1 c 3 c 9 c 15 c 11 c 13 c 12

Adjacency Graph c 14 c 5 c 2 c 7 c 8 c 10 c 3 c 6 c 9 c 11 c 13 c 12 c 4 c 2 c 15 c 14 c 7 c 15 c 8 c 11 c 10 c 3 c 6 c 9 c 13 c 12

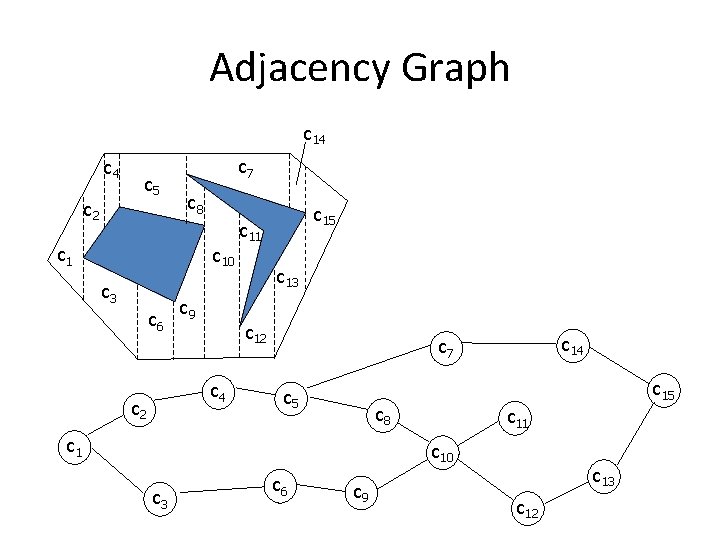
Path Planner • Search in adjacency graph for path from start cell to goal cell • First, find nodes in path

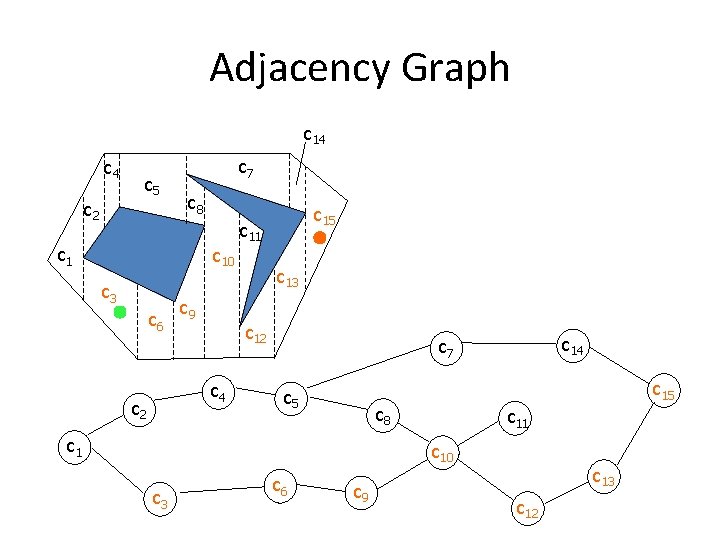
Adjacency Graph c 14 c 5 c 2 c 7 c 8 c 10 c 3 c 6 c 9 c 11 c 13 c 12 c 4 c 2 c 15 c 14 c 7 c 15 c 8 c 11 c 10 c 3 c 6 c 9 c 13 c 12

Creating a Path • Trapezoid is a convex set – Any two points on the boundary of a trapezoidal cell can be connected by a straight line segment that does not intersect any obstacle • Path is constructed by connecting midpoint of adjacency edges

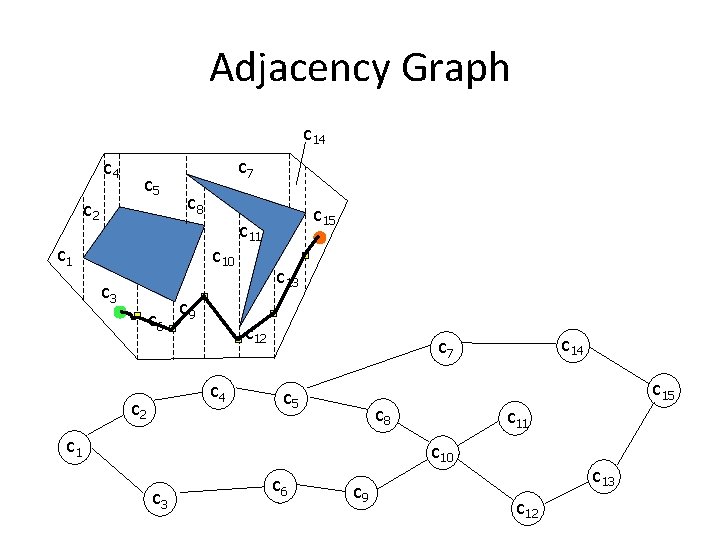
Adjacency Graph c 14 c 5 c 2 c 7 c 8 c 10 c 3 c 6 c 9 c 11 c 13 c 12 c 4 c 2 c 15 c 14 c 7 c 15 c 8 c 11 c 10 c 3 c 6 c 9 c 13 c 12

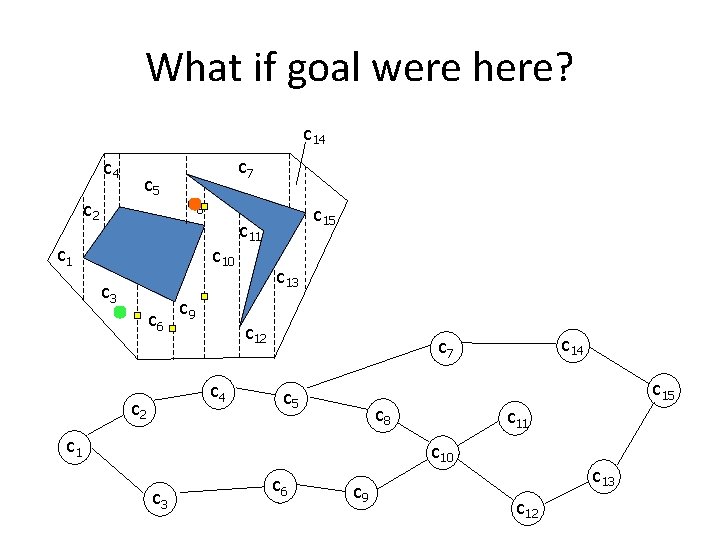
What if goal were here? c 14 c 5 c 2 c 7 c 8 c 10 c 3 c 6 c 9 c 11 c 13 c 12 c 4 c 2 c 15 c 14 c 7 c 15 c 8 c 11 c 10 c 3 c 6 c 9 c 13 c 12

Trapezoidal Decomposition • Shoot rays up and down from each vertex until they enter a polygon – Naïve approach O(n 2) (n vertices times n edges) c 14 c 5 c 2 c 7 c 8 c 10 c 3 c 6 c 9 c 15 c 11 c 13 c 12

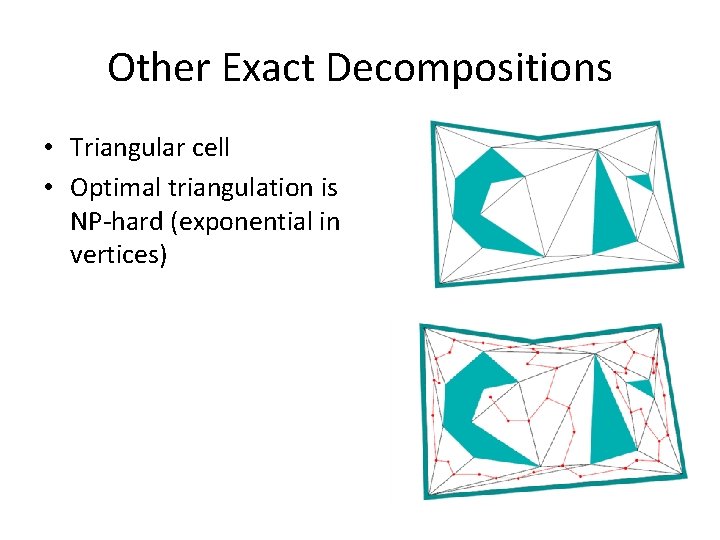
Other Exact Decompositions • Triangular cell • Optimal triangulation is NP-hard (exponential in vertices)