Viscous Flow in Ducts Computation of Discharge Coefficient

Problem Given: l The butterfly-valve losses may be viewed as a type of Bernoulli

Problem Asked: l Fit the average loss Kmean versus the opening angle to an

Assumptions l l l Incompressible flow Liquid Laminar flow

Opening Area l The opening area of the butterfly valve was found to be

Loss Coefficient Equation l A curve fit was used to find an equation for

Discharge Coefficient l The formula for discharge coefficient was derived from equation 6. 104

Discharge Coefficient l To reduce the discharge coefficient equation to an equation involving K

Discharge Coefficient l The discharge coefficient equation becomes: where β is the ratio of

Discharge Coefficient l After substituting the found values, the final discharge coefficient equation, as

Biomedical Application l The process used in determining the discharge coefficient of the valve

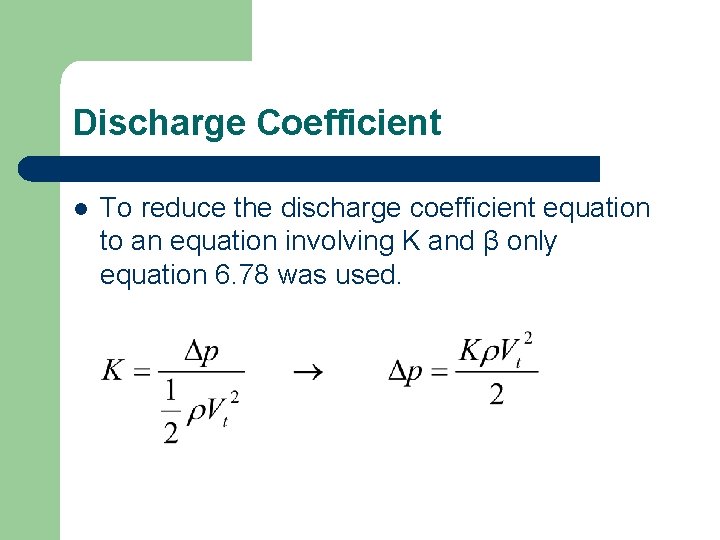
Slides: 13

Download presentation

Viscous Flow in Ducts Computation of Discharge Coefficient in Butterfly Valve John Grady David Ramezani Austin Thompson Problem *6. 160 BIEN 301 February 14, 2007

Problem Given: l The butterfly-valve losses may be viewed as a type of Bernoulli obstruction device. The "throat area" can be interpreted as the two slivers of opening around the butterfly disk when viewed from upstream.

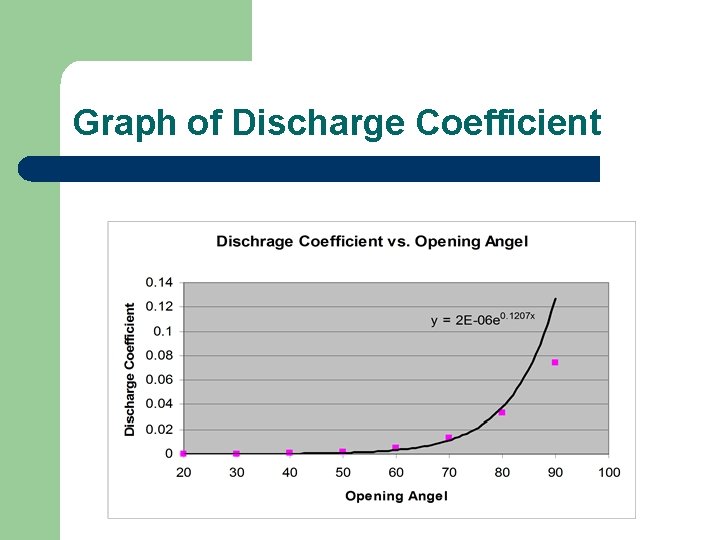
Problem Asked: l Fit the average loss Kmean versus the opening angle to an exponential curve. l Use your curve fit to compute the "discharge coefficient" of a butterfly valve as a function of the opening angle. l Plot the results and compare them to those for a typical flowmeter.

Assumptions l l l Incompressible flow Liquid Laminar flow

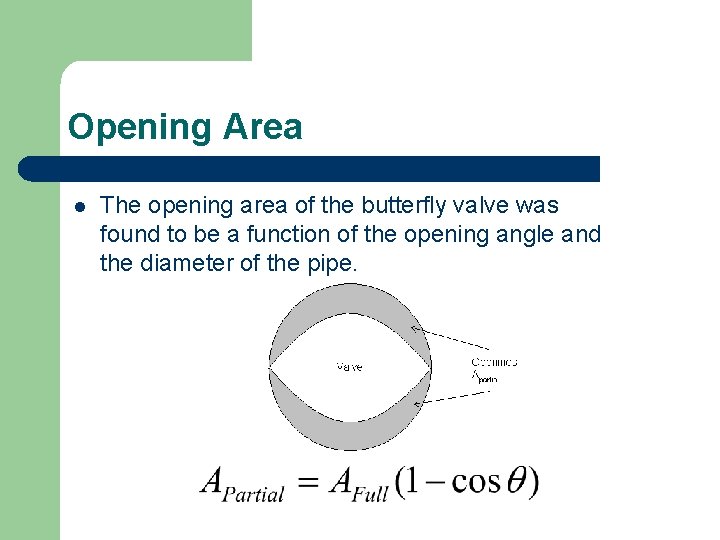
Opening Area l The opening area of the butterfly valve was found to be a function of the opening angle and the diameter of the pipe.

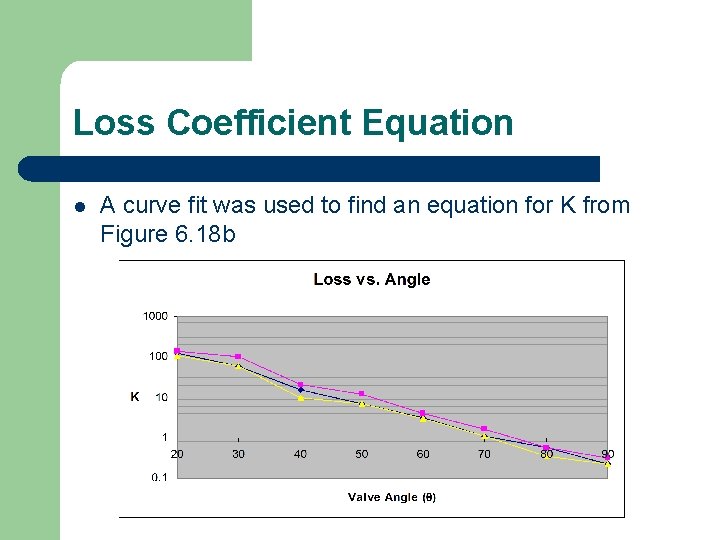
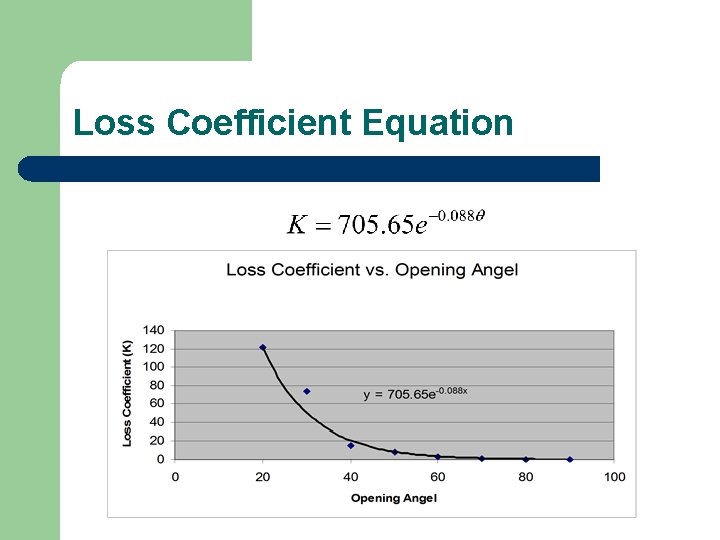
Loss Coefficient Equation l A curve fit was used to find an equation for K from Figure 6. 18 b

Loss Coefficient Equation

Discharge Coefficient l The formula for discharge coefficient was derived from equation 6. 104

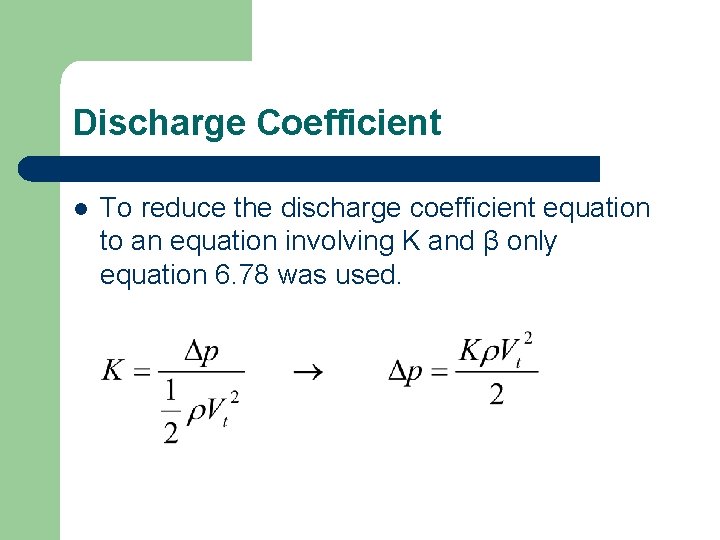
Discharge Coefficient l To reduce the discharge coefficient equation to an equation involving K and β only equation 6. 78 was used.

Discharge Coefficient l The discharge coefficient equation becomes: where β is the ratio of the partial area to the full area.

Discharge Coefficient l After substituting the found values, the final discharge coefficient equation, as a function of the opening angle, was found to be:

Graph of Discharge Coefficient

Biomedical Application l The process used in determining the discharge coefficient of the valve described in this problem could be applied to calculations regarding the heart. Since loss would be different in every heart, it may become necessary for a doctor to determine if a heart is functioning correctly, or in the design of a future prosthetic heart.