Virtuali kelion mokantis teorij sieti su praktinmis kompetencijomis


















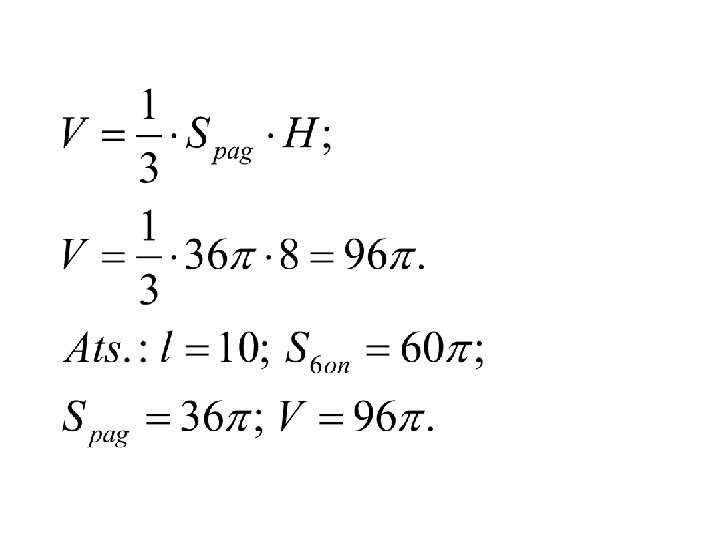












- Slides: 36

Virtuali kelionė mokantis teoriją sieti su praktinėmis kompetencijomis (Matematika, IT, Technologijos) Aušra Bogušienė Birytė Laurinaitienė Daiva Balčiūnienė Jūratė Burneikienė Šiaulių Stasio Šalkauskio gimnazija

Integracija ir kompetencijos Integruoto ugdymo galutinis tikslas – padėti mokiniui suprasti bendrąsias žmonijos vertybes, atskleisti ir realizuoti savo paties galimybes. Dalykų integravimas gerina ugdymo procesą, formuoja visuminį pasaulio pažinimą, stiprina mokinių žinias, padeda mokiniams aktyviau įsitraukti į mokymosi procesą. Per integruotas pamokas mokiniai atlieka įvairaus pobūdžio mokomąsias užduotis, ugdomas jų poreikis pažinti daugiau. Tokios pamokos padeda praktiškai pasitikrinti, kaip mokiniai geba taikyti įgytas žinias, kokius gebėjimus ir įgūdžius reikia patobulinti, kad būtų pasiektas norimas žinių lygis.

Projekto tikslai ir uždaviniai Lavinti erdvinę vaizduotę. Pajusti matematikos svarbą žmonių praktinės veiklos srityse. Skatinti norą diskutuoti, įvertinti savo ir kitų darbą. Pagal sudarytą technologinę schemą gaminti erdvinius kūnus. Tinkamai atrinkti darbo priemones ir medžiagas bei saugiai dirbti. Ugdyti mokinių kruopštumą, kūrybiškumą, originalumą. Lavinti bendravimo ir bendradarbiavimo kompetencijas. Skatinti mokinius naudoti kompiuterines mokymo priemones bei pažinti erdvinius kūnus virtualioje erdvėje. Gilinti ir tobulinti informacinių technologijų įgūdžius. Lavinti komunikacijos kompetenciją (darbų vertinimas, įsivertinimas bei pristatymas).

Reikalavimai įgyvendinant projektą Sukurkti brėžinį naudojantis kompiuterine mokymo priemone „Stereometrija ir erdviniai kūnai“. Jį išsaugoti dvejopai: sukurtos programos prievardžiu ir piešimo programos prievardžiu, uždavinio numeris - failo vardas (384. stk, 384. bmp). Užrašyti uždavinio sprendimą teksto redaktoriaus pagalba, atsižvelgiant į pateiktus reikalavimus. Užrašyti uždavinio sprendimą, sukuriant pateiktis, atsižvelgiant į pateiktus reikalavimus pateikčių rengimui. Pagaminti modelį (metalinį ar iš šiaudelių) nupaveiksluoti ir įkelti į pateiktis.

Darbo eiga

ØMatematikos pamokose mokiniai gavo konkretų uždavinį ir jį sprendė grupėje. Grupes sudarė nevienodų gabumų mokiniai. Gabesnieji mokiniai turėjo paaiškinti uždavinius silpnesniesiems. Taip mokiniai buvo mokomi pasitikėti savimi, tikėti mokymosi sėkme, pažinti savo mokymosi galimybes ir jas plėsti. Taip pat dalytis savo žiniomis ir įgyta patirtimi su kitais – jie mokėsi mokytis.

ØIT pamokose naudodami kompiuterinę programą „Stereometrija ir erdviniai kūnai“ braižė brėžinį pagal duotą sąlygą, aprašė uždavinio sprendimą teksto redaktoriumi, kūrė pateiktis. Šių pamokų metu mokiniai mokėsi kritiškai vertinti informacinių ir komunikacinių technologijų galimybes ir privalumus, atsakingai taikyti šias technologijas, noriai ir kūrybiškai taikyti sudėtingesnes teksto tvarkymo kompiuteriu galimybes mokantis ir kitoje veikloje.

ØTechnologijų pamokose gamino erdvinius kūnus iš plastikinių šiaudelių. Susidomėję ir turintys galimybes mokiniai galėjo pratęsti darbą namuose ir kartu su tėveliais pagaminti erdvinius kūnus naudodami kitokias medžiagas bei priemones. Šis darbas susiejo teorines žinias su praktika. Mokiniai mokėsi tolerantiškai, kūrybingai bendradarbiauti, pasitikėti savo jėgomis, iniciatyviai, atsakingai, racionaliai, kūrybingai spręsti problemas, rūpintis savo ir kitų saugumu.

ØBaigiamasis etapas vyko matematikos pamokoje. Pristatomus mokinių darbus stebėjo, aptarė ir vertino integruotų dalykų mokytojai (matematikos, informacinių technologijų, technologijų) bei pamokoje dalyvaujantys mokiniai. Mokiniai dirbo noriai, parengė įdomius, tvarkingus, pristatymus. Dauguma mokinių sužinojo naujų ir įdomių dalykų, išmoko atrinkti informaciją, naudotis įvairiais informacijos šaltiniais bei teorines žinias pritaikyti praktikoje.

Mokinių darbai

Šioje nuotraukoje mokiniai konstruoja iš spalvotų plastikinių šiaudelių erdvinius kūnus.



Šioje nuotraukoje mokiniai sutvirtina konstrukcijas karštų klijų pagalba.


Šiose nuotraukose mokiniai konstravo erdvinius kūnus iš metalinių virbų, padedami tėvų.

Taisyklingoji trikampė piramidė Ingrida Domeikytė Kristina Liaugaudaitė Evelina Bičkutė 9 e klasė ingri 0117@yahoo. com

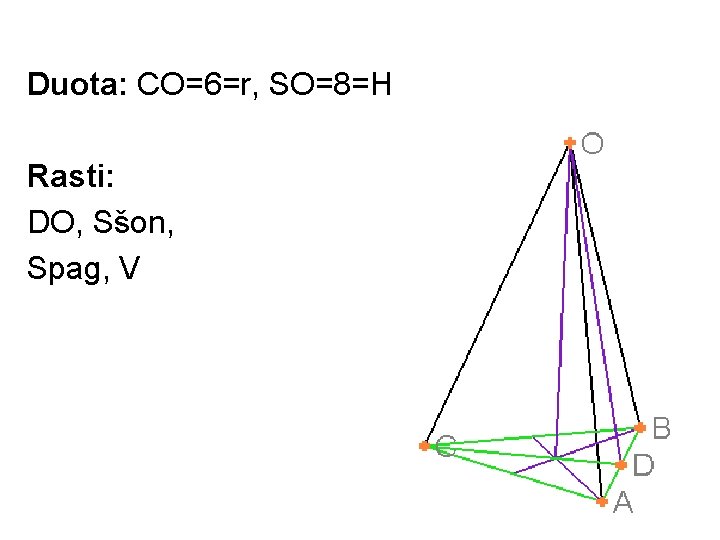
370. Duota: taisyklingoji trikampė piramidė SABC, kurios briauna lygi 10. Taškas D yra briaunos AB vidurio taškas. SO yra piramidės aukštinė. Apskaičiuokite SC, Sšon, Spag, V.

Duota: CO=6=r, SO=8=H Rasti: DO, Sšon, Spag, V

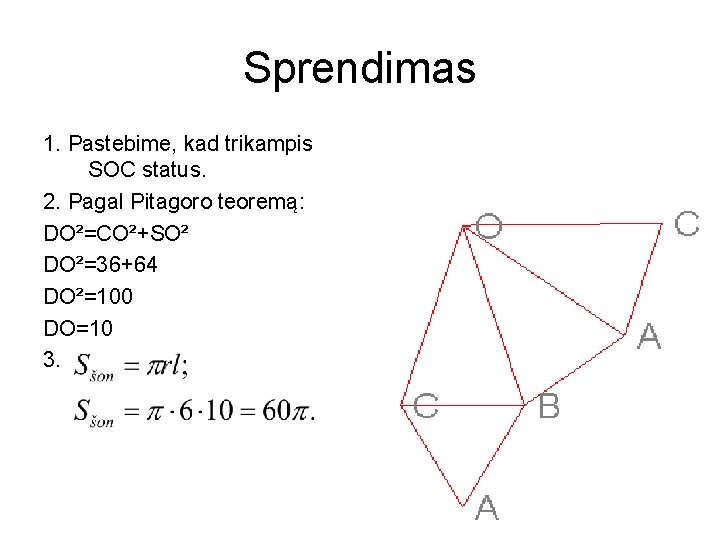
Sprendimas 1. Pastebime, kad trikampis SOC status. 2. Pagal Pitagoro teoremą: DO²=CO²+SO² DO²=36+64 DO²=100 DO=10 3.
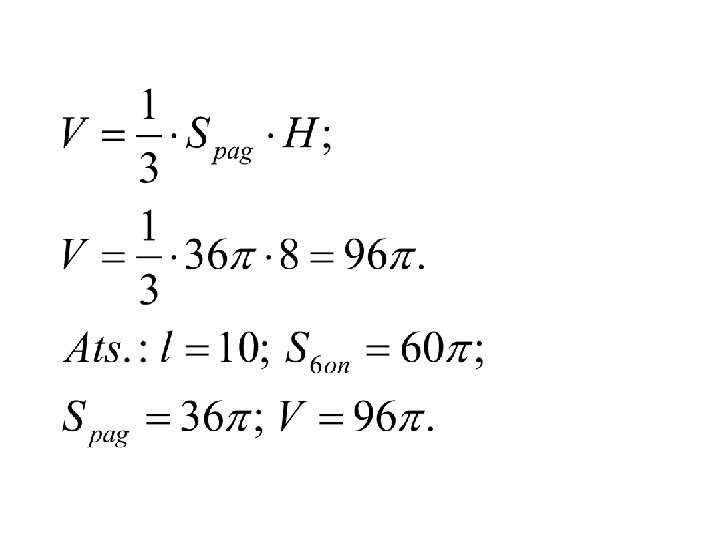

Šaltiniai ir naudotos programos • • Matematika, 9 klasė, ll dalis Microsoft Power. Point Microsoft Word Stereometrija

Matematikos uždavinys Darbą parengė: Vytautas Stankūnas 9 d, Gabrielė Pilipavičiūtė 9 d, Martyna Pociutė 9 d www. wytkez@gmail. com

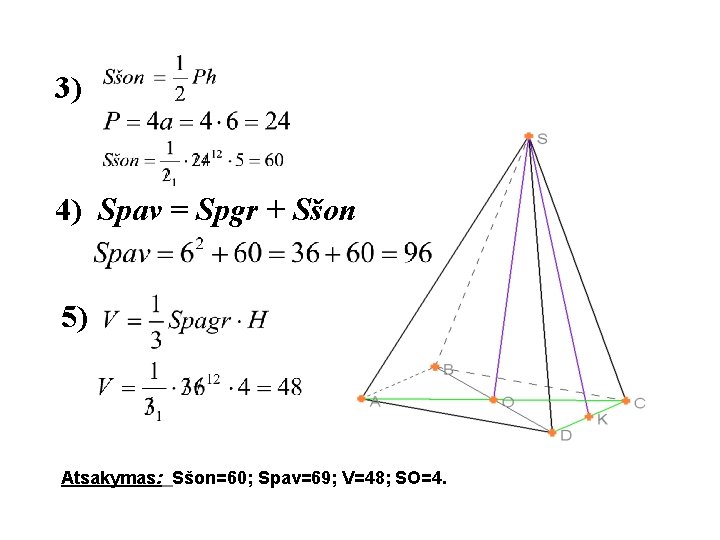
Uždavinys 382. Sąlyga: Taisyklingosios keturkampės piramidės pagrindo kraštinė yra a, aukštinė – H, apotema – h, šoninis paviršius – Sšon, visas paviršius – Spav, tūris – V. Išspręsti uždavinio a) dalį.

Duota: SABCD – piramidė; ABCD – kvadratas; AD = 6; SK = 5. Rasti: Sšon; Spav; V; SO.

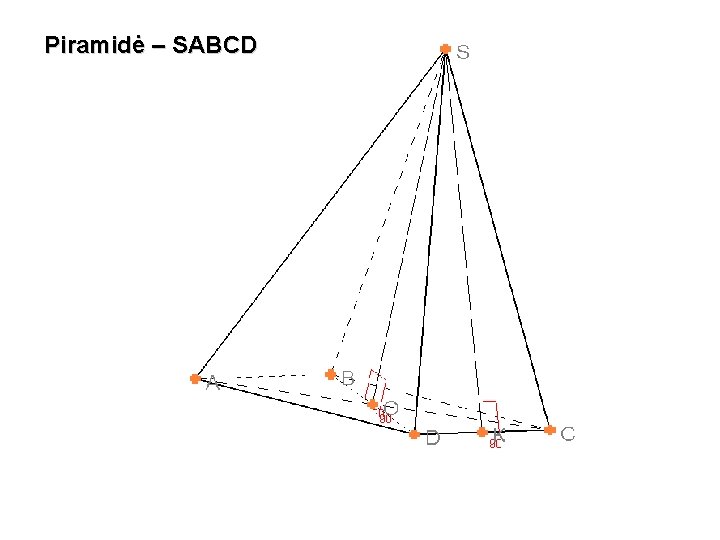
Piramidė – SABCD

Sprendimas: 1) OK = AD : 2 S OK = 6 : 2 = 3 2) Pagal Pitagoro teoremą. 5 O 3 K

3) 4) Spav = Spgr + Sšon 5) Atsakymas: Sšon=60; Spav=69; V=48; SO=4.

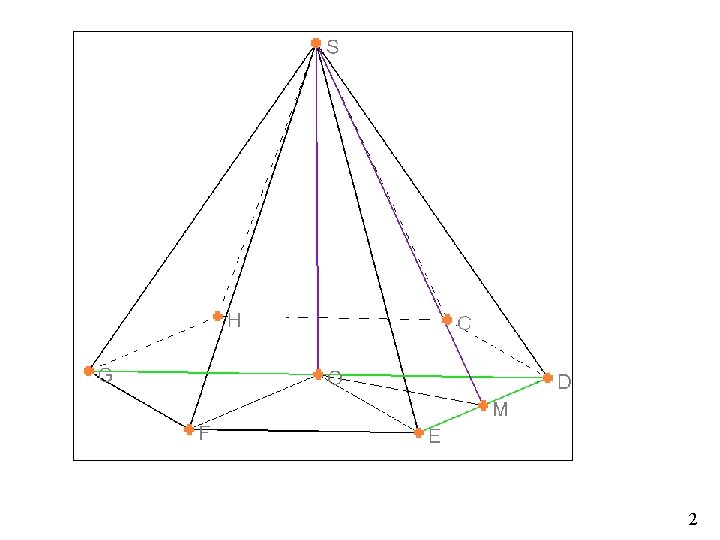
Greta Skiparytė Armanda Vinickaitė 9 d klasė 386. a) Taisyklingosios šešiakampės piramidės pagrindo kraštinė yra a, o aukštine yra - H. Apskaičiuokite šios piramidės šoninio paviršiaus plotą, viso paviršiaus plotą ir tūrį.

2

Duota: SCDEFGM – šešiakampė piramidė H = 14 dm a= 8 dm Rasti : Sšon. Spav. V 3

Štai pagamintos šešiakampės piramidės nuotrauka:

Sprendimas: FOE- lygiakraštis FL=LF= 8: 2=4 (dm) Pagal Pitagoro teoremą 4

Pagal Pitagoro teoremą: 5

Išvados Ø Mokiniai yra skirtingi – integravus ugdymo procesą geriau tenkinami kiekvieno vaiko poreikiai, sudaromos optimaliausios sąlygos saviraiškai; Ø Įvairūs integruotojo ugdymo metodai, būdai ir modeliai padeda ugdyti mokinio kompetencijas, reikalingas visuomenėje; Ø Ugdymo proceso grandys sujungtos į darnią visumą, todėl mokiniai susidaro vientisą vaizdą, greičiau ir geriau ima suvokti esmę. Ø Mokiniai komunikavo (pagarbiai, argumentuotai išsakė savo nuomonę pasirinkdami aktualią informaciją, diskutavo apie reikalingos informacijos tikslingą pasirinkimą); plėtė savo technologinius įgūdžius, mokėsi mokytis, bendradarbiavo, naudojo informacines komunikacines technologijas.

Dėkui už dėmesį!