Virtual COMSATS Inferential Statistics Lecture20 Ossam Chohan Assistant

Virtual COMSATS Inferential Statistics Lecture-20 Ossam Chohan Assistant Professor CIIT Abbottabad 1

Recap of last lecture • In our last sessions, we worked on: – Overview of statistical inferences – Hypothesis testing introduction. – Six steps of Hypothesis testing. – Problems regarding single mean and proportion using z and t statistics. 2

Objective of lecture-20 • In this lecture, we will understand problems related to difference between two populations: – Dependent samples. – Independent samples. – Proportions case. – Some portion of Chi-square distribution. 3

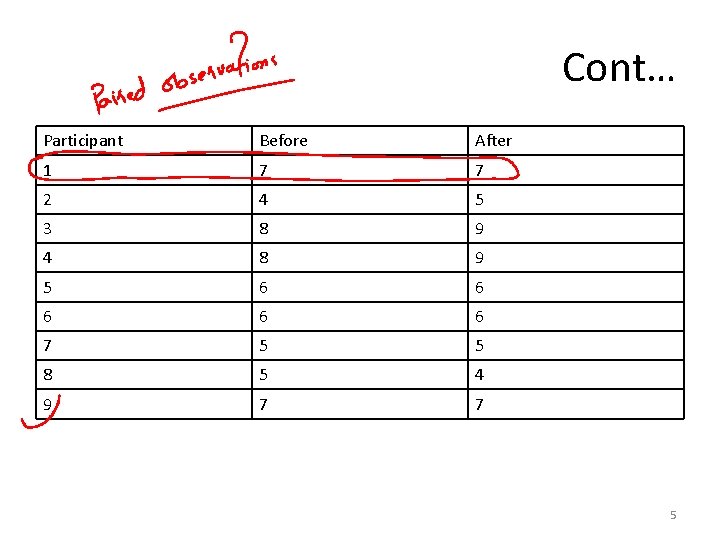
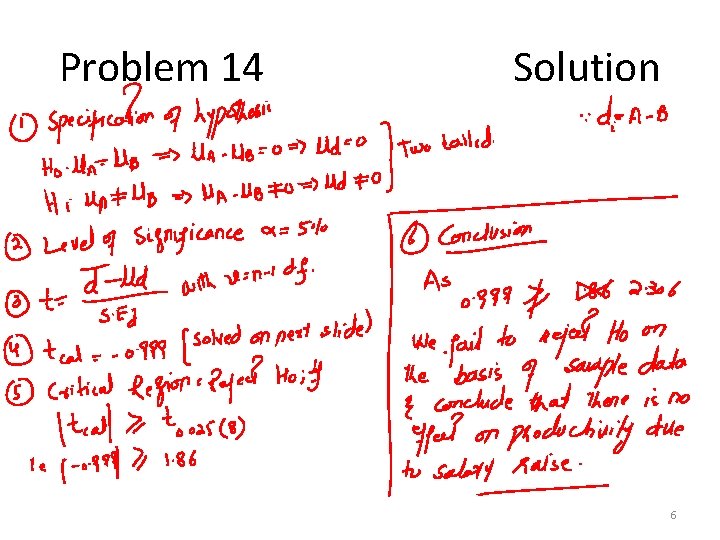
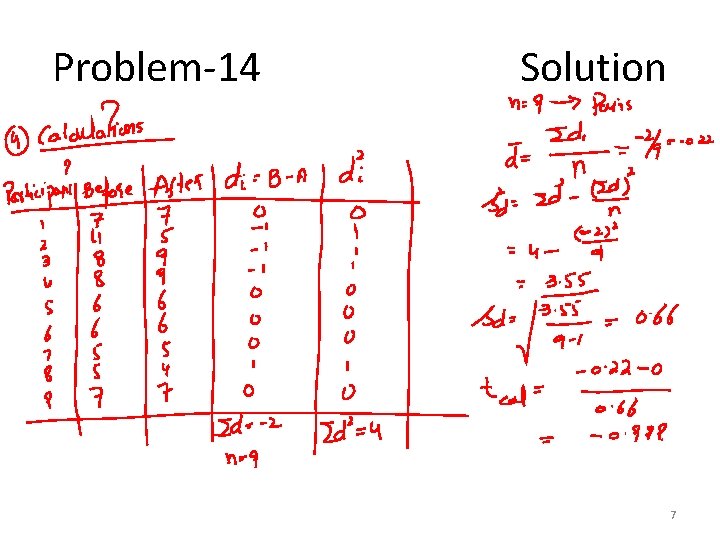
Problem-14 • A researcher interested in employee satisfaction and productivity measured the number of units produced by employees at a plant before and after a company-wide pay raise occurred. The researcher hypothesized that production would be higher after the raise compared to before the raise. Assume that the difference scores are normally distributed and let a = 0. 05. 4

Cont… Participant Before After 1 7 7 2 4 5 3 8 9 4 8 9 5 6 6 6 7 5 5 8 5 4 9 7 7 5

Problem 14 Solution 6

Problem-14 Solution 7

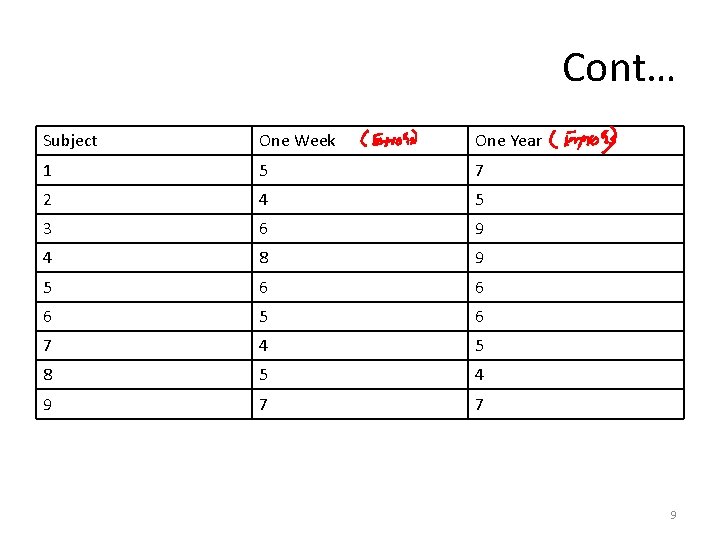
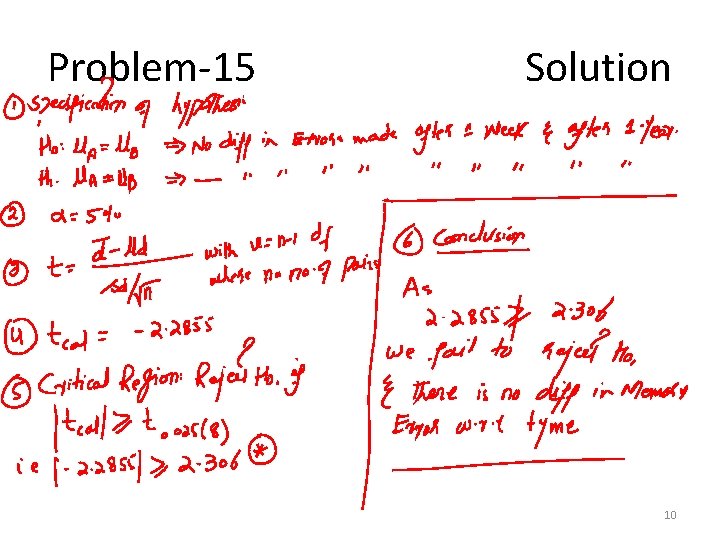
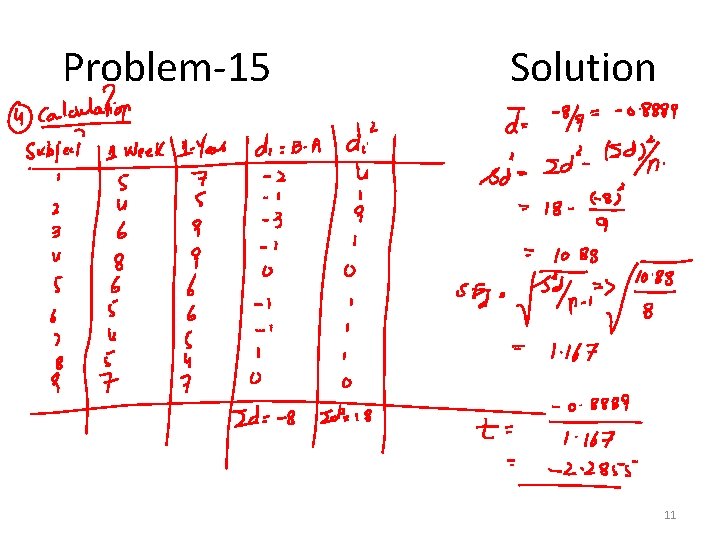
Problem-15 • A sociologist is interested in the decay of long-term memory compared to the number of errors in memory that an individual made after 1 week and after 1 year for a specific crime event. Participants viewed a videotape of a bank robbery and were asked a number of specific questions about the video 1 week after viewing it. They were asked the same questions 1 year after seeing the video. The number of memory errors was recorded for each participant at each time period. The researchers asked whether or not there was a significant difference in the number of errors in the two time periods. Assume that the difference scores are normally distributed and let α = 0. 05. 8

Cont… Subject One Week One Year 1 5 7 2 4 5 3 6 9 4 8 9 5 6 6 6 5 6 7 4 5 8 5 4 9 7 7 9

Problem-15 Solution 10

Problem-15 Solution 11

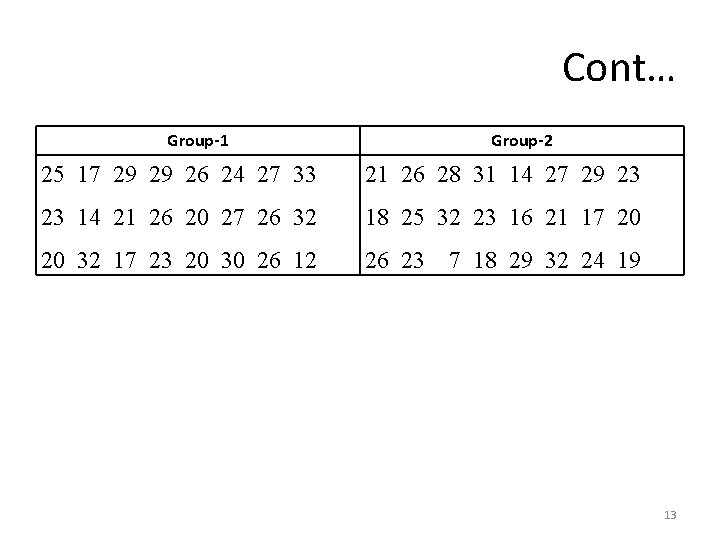
Assessment Problem-13 • Suppose you are interested in developing a counseling technique to reduce stress within marriages. You randomly select two samples of married individuals out of ten churches in the association. You provide Group 1 with group counseling and study materials. You provide Group 2 with individual counseling and study materials. • At the conclusion of the treatment period, you measure the level of marital stress in the group members. Here are the scores: 12

Cont… Group-1 Group-2 25 17 29 29 26 24 27 33 21 26 28 31 14 27 29 23 23 14 21 26 20 27 26 32 18 25 32 23 16 21 17 20 20 32 17 23 20 30 26 12 26 23 7 18 29 32 24 19 13

CHI-SQUARE DISTRIBUTION χ2 14

Objective • In this part of the course students will understand learn the following topics: Ø Chi square and its properties Ø Chi square as a test of independence Ø Chi square as a test of goodness of fit 15

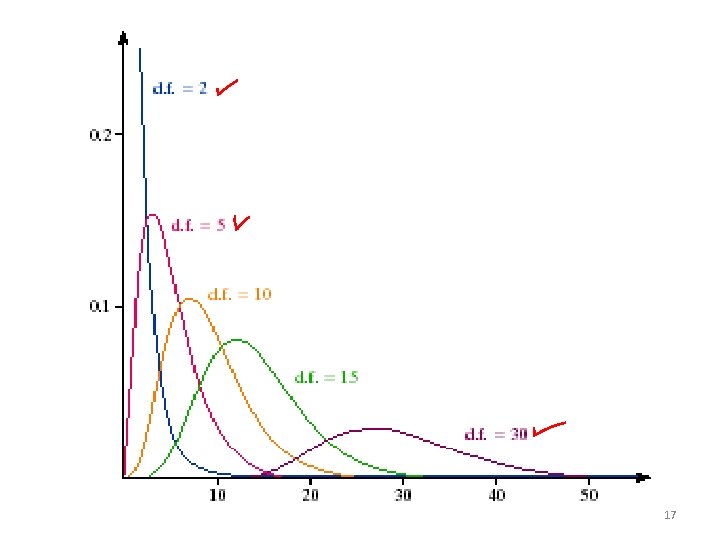
PROPERTIES OF CHI-SQUARE • Chi-square is a continuous distribution ranging from 0 to infinity • It depends upon degrees of freedom, • It is not symmetric. • As the number of degrees of freedom increases, the chi-square distribution becomes more symmetric. • The values are non-negative. That is, the values of are greater than or equal to 0. • The mean of chi-square distribution is its degree of freedom. 16

17

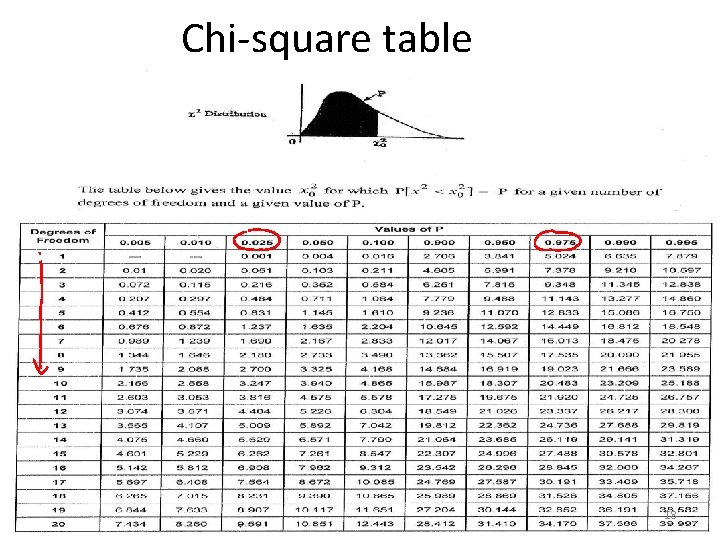
Chi-square table 18

• Each χ2 distribution has a degree of freedom associated with it, so that there are many different chi squared distributions. • The chi squared distributions for each of 1 through 20 degrees of freedom are shown in the table. 19

USES • Chi square is used for testing: – Variance – Confidence interval for variances – Independence between two categorical variables – Homogeneity – Association between attributes. – Two proportions – Many proportions testing. – And many more applications in research. 20

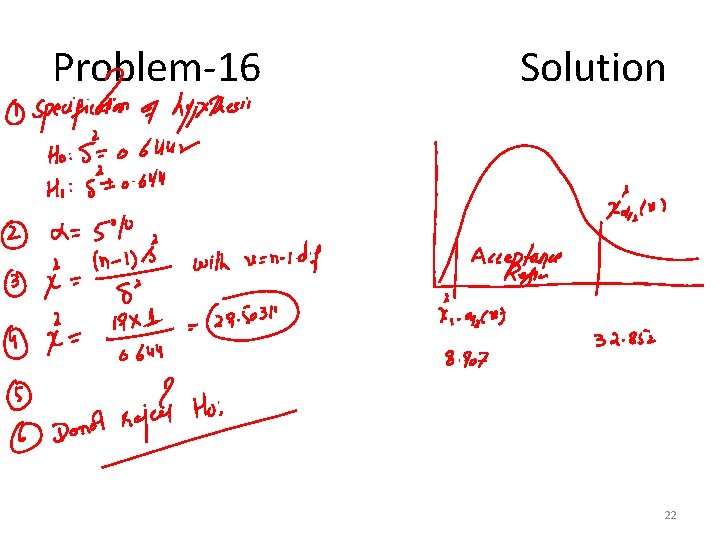
Problem-16 • A cigarette manufacturer wants to test the claim that the variance of the nicotine content of its cigs. is 0. 644 milligram. Assume that it is normally distributed. A sample of 20 cigs. has a standandard deviation of 1. 00 milligram. At α = 0. 05, is there sample evidence to reject the manufacturer's claim? 21

Problem-16 Solution 22

Problem-17 • A machine dispenses a liquid drug into bottles in such a way that the standard deviation of the contents is 81 milliliters. A new machine is tested on a sample of 24 containers and the standard deviation for this sample group is found to be 26 milliliters. At the 0. 05 level of significance, test the claim that the amount dispensed by the new machine have a smaller standard deviation. 23

Problem-17 Solution 24

Assessment Problem-14 • For randomly selected adults, IQ scores are normally distributed with a standard deviation of 16. The scores of 15 randomly selected college students are listed below. Use a 0. 10 significance level to test the claim that the standard deviation of IQ scores of college students is less than 16. HINT: calculate ‘s’ for the 15 college students listed below. • 115 128 107 116 118 126 129 124 135 127 115 104 133 25