Viewing Projection in Web GL covered in the

Viewing & Projection in Web. GL covered in the previous lecture

Example 1: Rotating Cube

For Further Reading • Angel 7 th Ed: – Chapter 5 • Beginning Web. GL: – Chapter 1 : Viewing Part II • http: //glmatrix. net/ – Javascript Matrix and Vector library for High Performance Web. GL apps. 3

Viewing and Projection

Classical Viewing • Viewing requires three basic elements One or more objects A viewer with a projection surface Projectors that go from the object(s) to the projection surface • Classical views are based on the relationship among these elements The viewer picks up the object and orients it how she would like to see it • Each object is assumed to constructed from flat principal faces Buildings, polyhedra, manufactured objects Angel: Interactive Computer Graphics 4 E © Addison-Wesley 5

Planar Geometric Projections • Standard projections project onto a plane • Projectors are lines that either converge at a center of projection are parallel • Such projections preserve lines but not necessarily angles • Nonplanar projections are needed for applications such as map construction Angel: Interactive Computer Graphics 4 E © Addison-Wesley 6

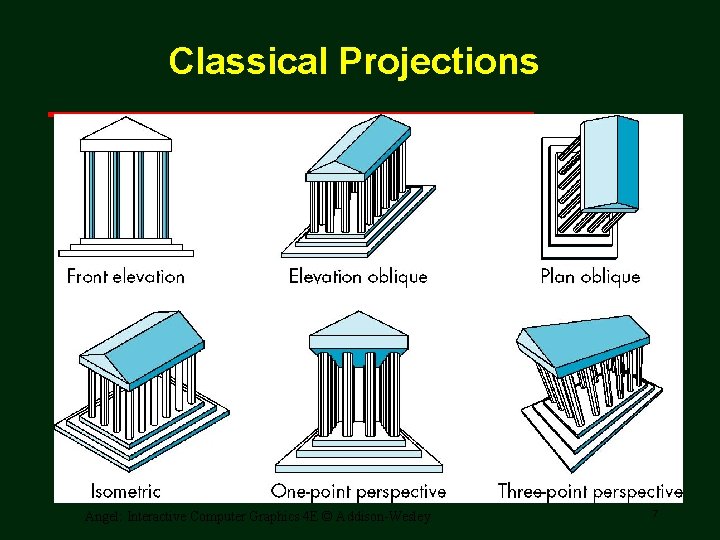
Classical Projections Angel: Interactive Computer Graphics 4 E © Addison-Wesley 7

Perspective vs Parallel • Computer graphics treats all projections the same and implements them with a single pipeline • Classical viewing developed different techniques for drawing each type of projection • Fundamental distinction is between parallel and perspective viewing even though mathematically parallel viewing is the limit of perspective viewing Angel: Interactive Computer Graphics 4 E © Addison-Wesley 8

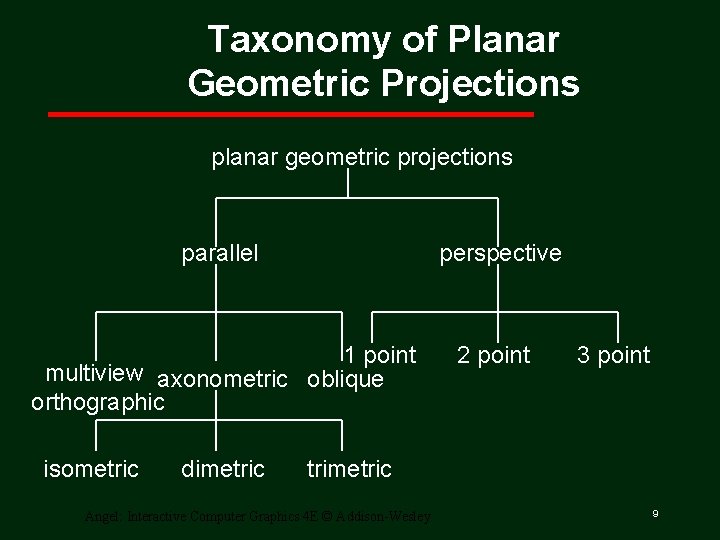
Taxonomy of Planar Geometric Projections planar geometric projections perspective parallel 1 point multiview axonometric oblique orthographic isometric dimetric 2 point 3 point trimetric Angel: Interactive Computer Graphics 4 E © Addison-Wesley 9

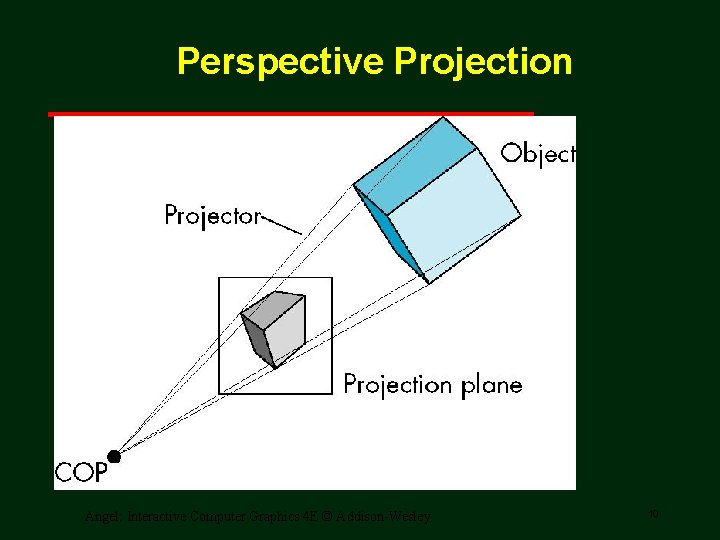
Perspective Projection Angel: Interactive Computer Graphics 4 E © Addison-Wesley 10

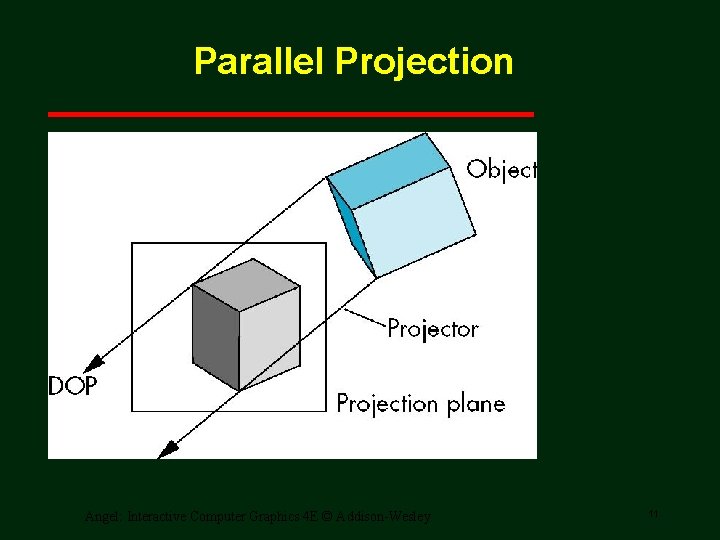
Parallel Projection Angel: Interactive Computer Graphics 4 E © Addison-Wesley 11

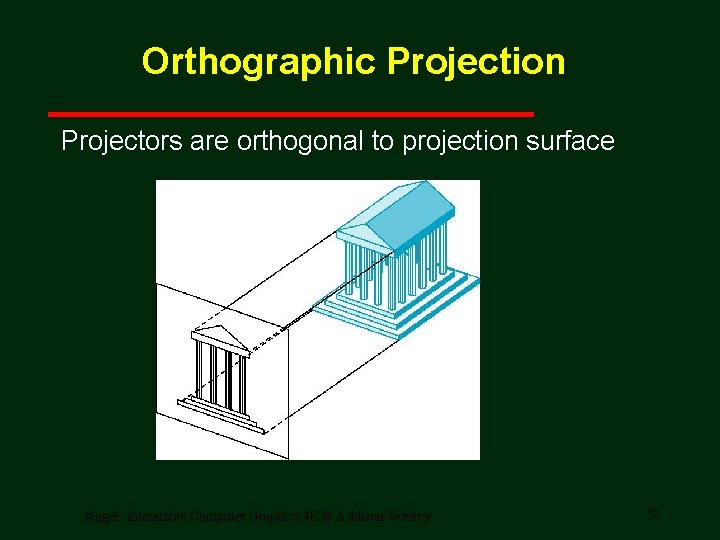
Orthographic Projection Projectors are orthogonal to projection surface Angel: Interactive Computer Graphics 4 E © Addison-Wesley 12

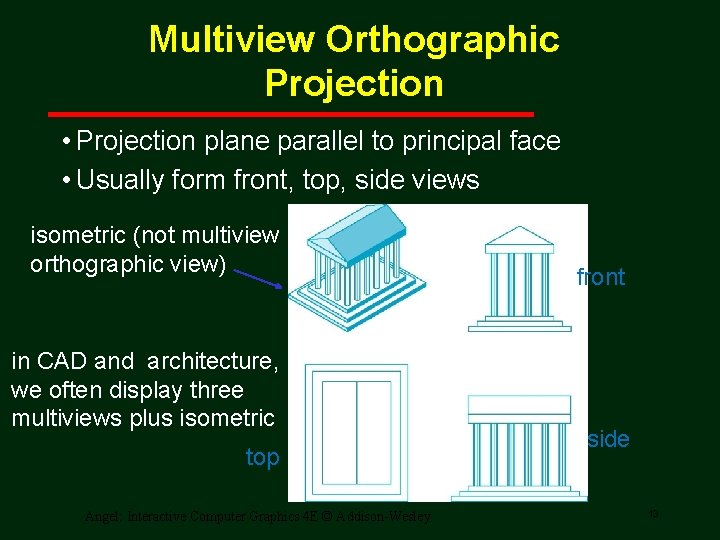
Multiview Orthographic Projection • Projection plane parallel to principal face • Usually form front, top, side views isometric (not multiview orthographic view) in CAD and architecture, we often display three multiviews plus isometric top Angel: Interactive Computer Graphics 4 E © Addison-Wesley front side 13

Advantages and Disadvantages • Preserves both distances and angles Shapes preserved Can be used for measurements • Building plans • Manuals • Cannot see what object really looks like because many surfaces hidden from view Often we add the isometric Angel: Interactive Computer Graphics 4 E © Addison-Wesley 14

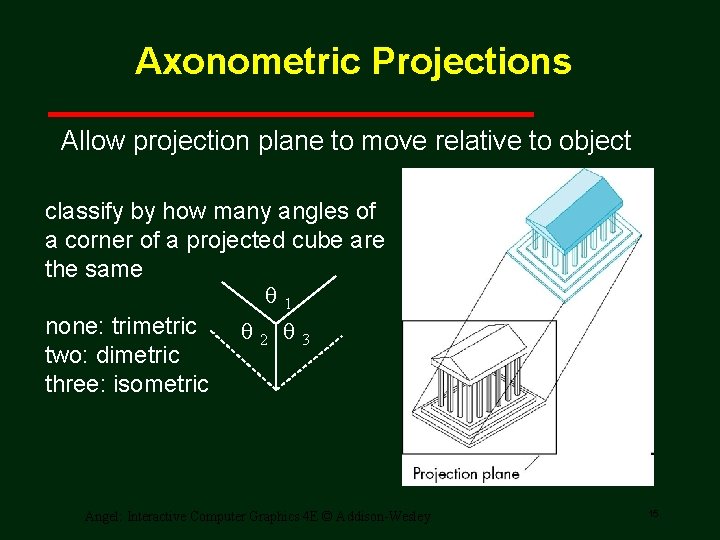
Axonometric Projections Allow projection plane to move relative to object classify by how many angles of a corner of a projected cube are the same q 1 none: trimetric q 2 q 3 two: dimetric three: isometric Angel: Interactive Computer Graphics 4 E © Addison-Wesley 15

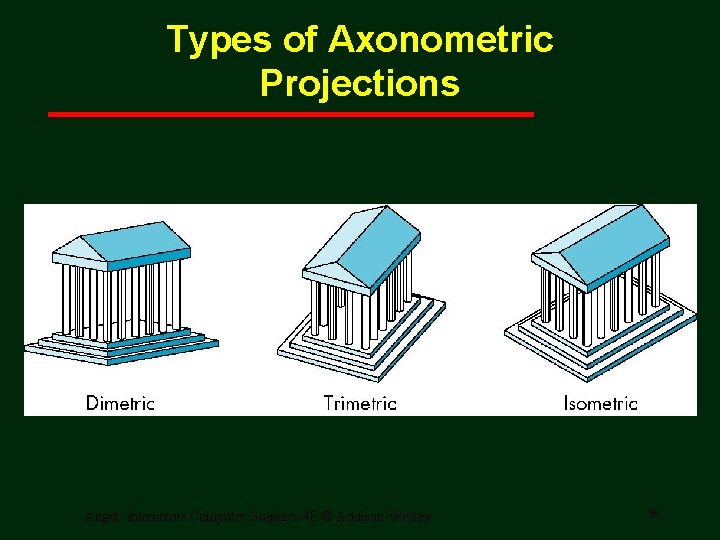
Types of Axonometric Projections Angel: Interactive Computer Graphics 4 E © Addison-Wesley 16

Advantages and Disadvantages • Lines are scaled (foreshortened) but can find scaling factors • Lines preserved but angles are not Projection of a circle in a plane not parallel to the projection plane is an ellipse • Can see three principal faces of a box like object • Some optical illusions possible Parallel lines appear to diverge • Does not look real because far objects are scaled the same as near objects • Used in CAD applications Angel: Interactive Computer Graphics 4 E © Addison-Wesley 17

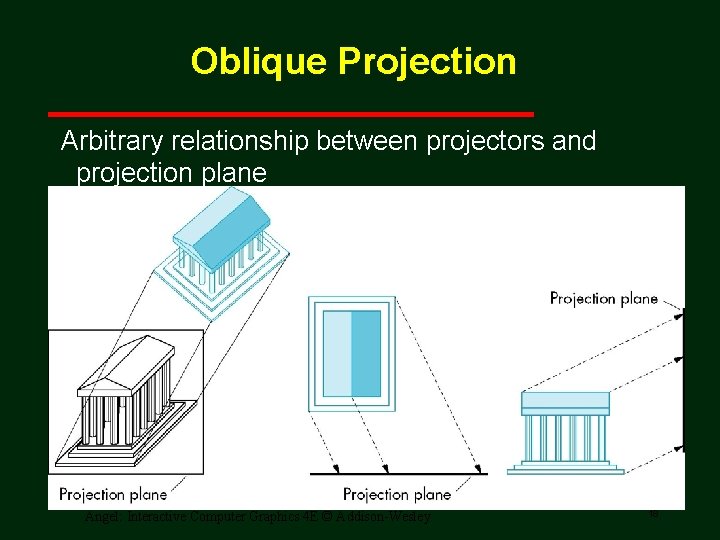
Oblique Projection Arbitrary relationship between projectors and projection plane Angel: Interactive Computer Graphics 4 E © Addison-Wesley 18

Advantages and Disadvantages • Can pick the angles to emphasize a particular face Architecture: plan oblique, elevation oblique • Angles in faces parallel to projection plane are preserved while we can still see “around” side • In physical world, cannot create with simple camera; possible with bellows camera or special lens (architectural) Angel: Interactive Computer Graphics 4 E © Addison-Wesley 19

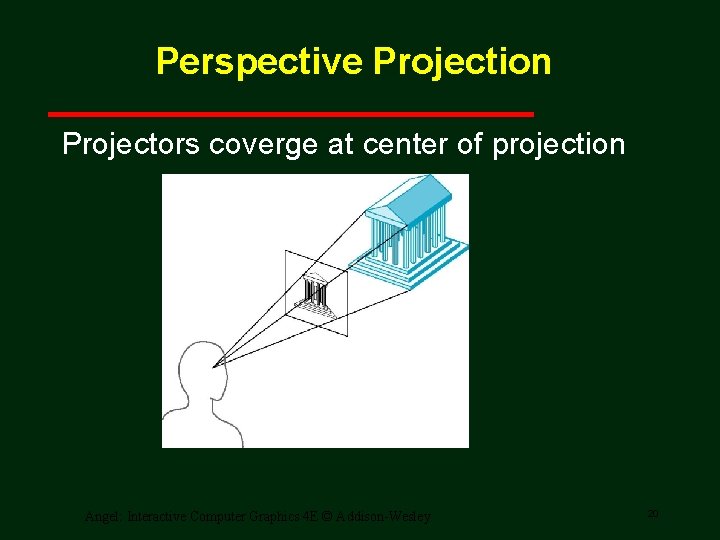
Perspective Projection Projectors coverge at center of projection Angel: Interactive Computer Graphics 4 E © Addison-Wesley 20

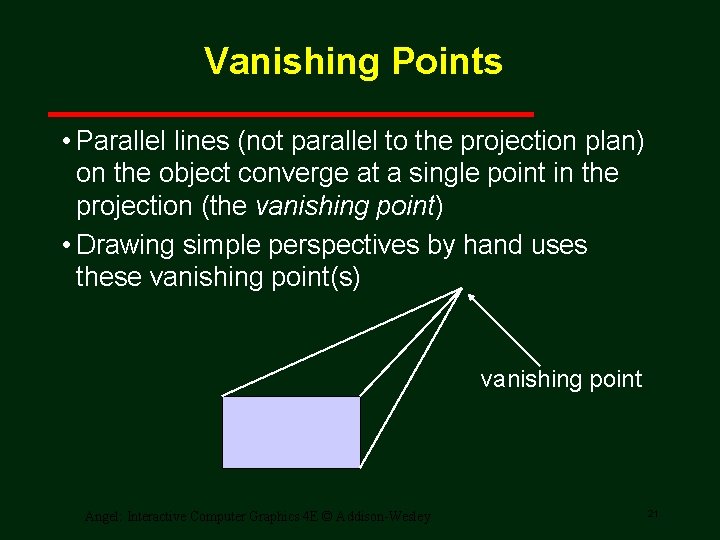
Vanishing Points • Parallel lines (not parallel to the projection plan) on the object converge at a single point in the projection (the vanishing point) • Drawing simple perspectives by hand uses these vanishing point(s) vanishing point Angel: Interactive Computer Graphics 4 E © Addison-Wesley 21

Three-Point Perspective • No principal face parallel to projection plane • Three vanishing points for cube Angel: Interactive Computer Graphics 4 E © Addison-Wesley 22

Two-Point Perspective • On principal direction parallel to projection plane • Two vanishing points for cube Angel: Interactive Computer Graphics 4 E © Addison-Wesley 23

One-Point Perspective • One principal face parallel to projection plane • One vanishing point for cube Angel: Interactive Computer Graphics 4 E © Addison-Wesley 24

Advantages and Disadvantages • Objects further from viewer are projected smaller than the same sized objects closer to the viewer (diminution) Looks realistic • Equal distances along a line are not projected into equal distances (nonuniform foreshortening) • Angles preserved only in planes parallel to the projection plane • More difficult to construct by hand than parallel projections (but not more difficult by computer) Angel: Interactive Computer Graphics 4 E © Addison-Wesley 25

Computer Viewing • There are three aspects of the viewing process, all of which are implemented in the pipeline, Positioning the camera • Setting the model view matrix Selecting a lens • Setting the projection matrix Clipping • Setting the view volume Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 26

The Web. GL Camera • In Web. GL, initially the object and camera frames are the same Default model view matrix is an identity • The camera is located at origin and points in the negative z direction • Web. GL also specifies a default view volume that is a cube with sides of length 2 centered at the origin Default projection matrix is an identity Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 27

Right-Hand vs. Left-Hand Rule Image source: http: //en. wikipedia. org/wiki/File: Cartesian_coordinate_system_handedness. svg This file is licensed under the Creative Commons Attribution-Share Alike 3. 0 Unported license. 28

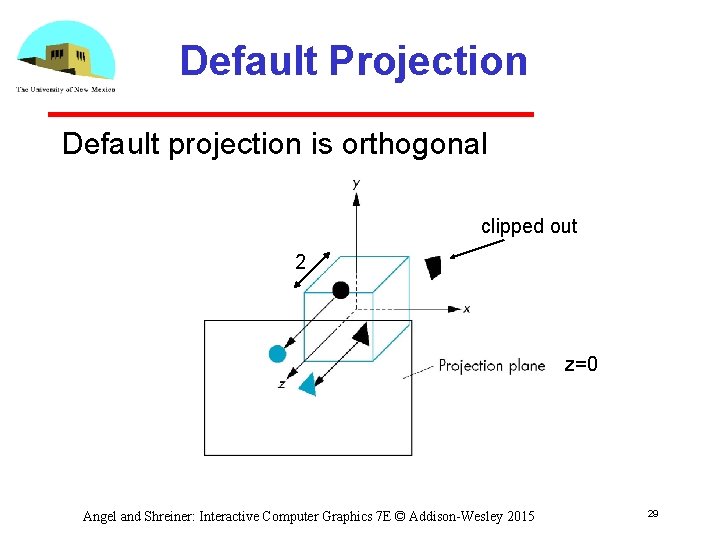
Default Projection Default projection is orthogonal clipped out 2 z=0 Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 29

Moving the Camera Frame • If we want to visualize objects with both positive and negative z values we can either Move the camera in the positive z direction • Translate the camera frame Move the objects in the negative z direction • Translate the world frame • Both of these views are equivalent and are determined by the model view matrix Want a translation (translate(0. 0, -d); ) d > 0 Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 30

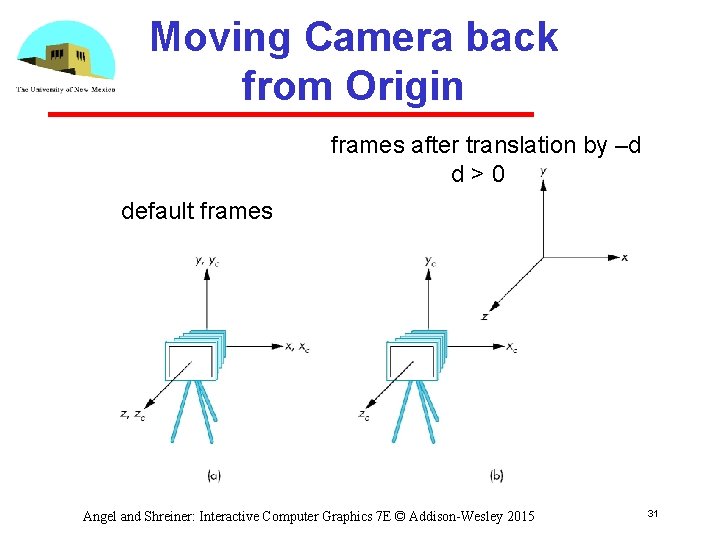
Moving Camera back from Origin frames after translation by –d d>0 default frames Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 31

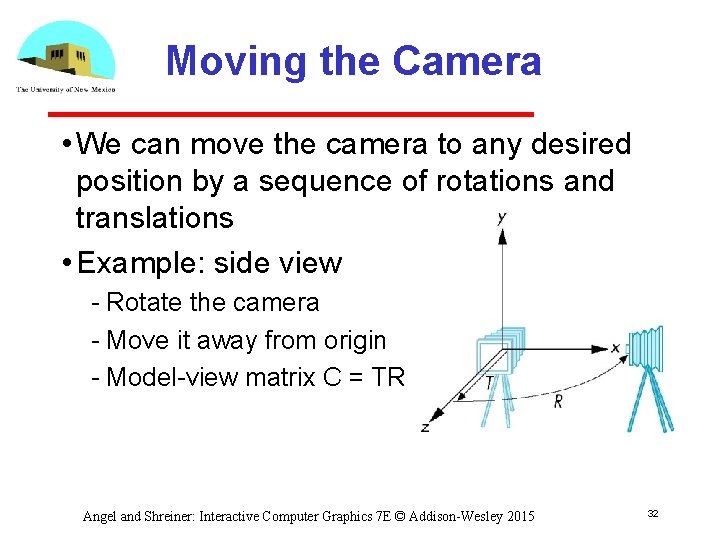
Moving the Camera • We can move the camera to any desired position by a sequence of rotations and translations • Example: side view Rotate the camera Move it away from origin Model view matrix C = TR Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 32

Web. GL code • Remember that last transformation specified is first to be applied // Using MV. js var t = translate (0. 0, -d); var ry = rotate. Y(90. 0); var m = mult(t, ry); or var m = mult(translate (0. 0, -d), rotate. Y(90. 0); ); Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 33

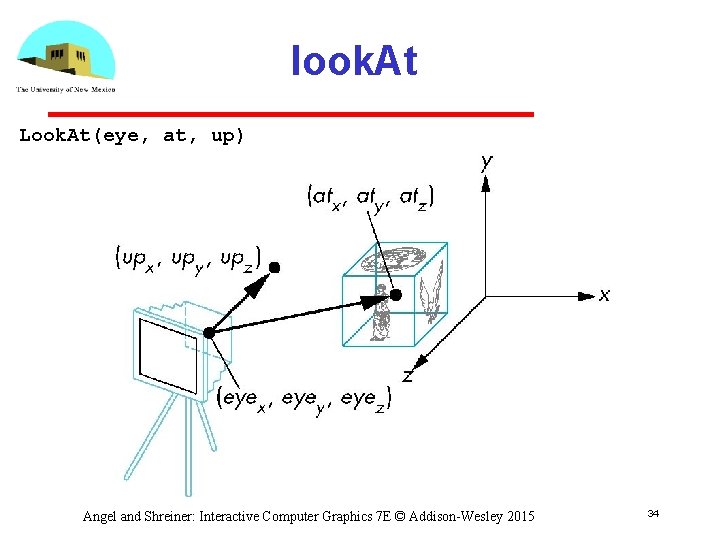
look. At Look. At(eye, at, up) Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 34

The look. At Function • The GLU library contained the function glu. Look. At to form the required modelview matrix through a simple interface • Note the need for setting an up direction • Replaced by look. At() in MV. js Can concatenate with modeling transformations • Example: isometric view of cube aligned with axes var var eye = vec 3(1. 0, 1. 0); at = vec 3(0. 0, 0. 0); up = vec 3(0. 0, 1. 0, 0. 0); mv = Look. At(eye, at, up); Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 35

• Now, we have determined how the objects are placed relative to the camera. • But we haven’t defined how the objects are projected to the image.

(Orthogonal) Projection and Normalization • The default projection in the eye (camera) frame is orthogonal • For points within the default view volume xp = x yp = y zp = 0 • Most graphics systems use view normalization All other views are converted to the default view by transformations that determine the projection matrix Allows use of the same pipeline for all views Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 37

Homogeneous Coordinate Representation xp = x yp = y zp = 0 wp = 1 pp = Mp M= In practice, we can let M = I and set the z term to zero later Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 38

Perspective 39

40

Simple Perspective • Center of projection at the origin • Projection plane z = d, d < 0 Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 41

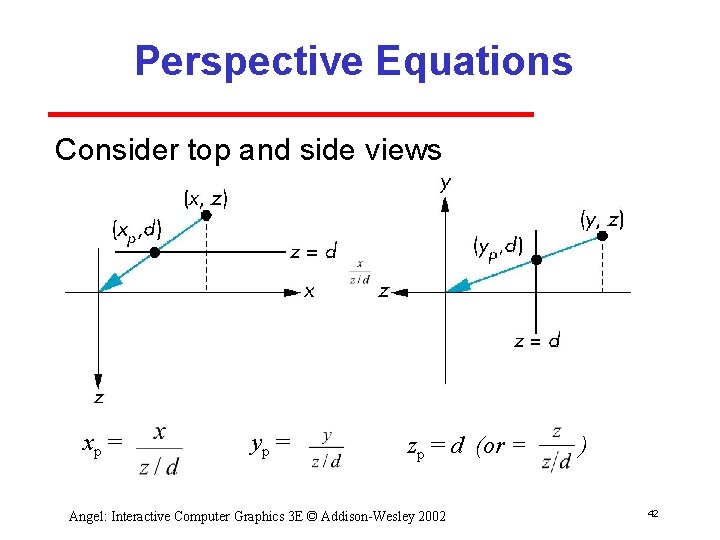
Perspective Equations Consider top and side views xp = yp = zp = d (or = Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 ) 42

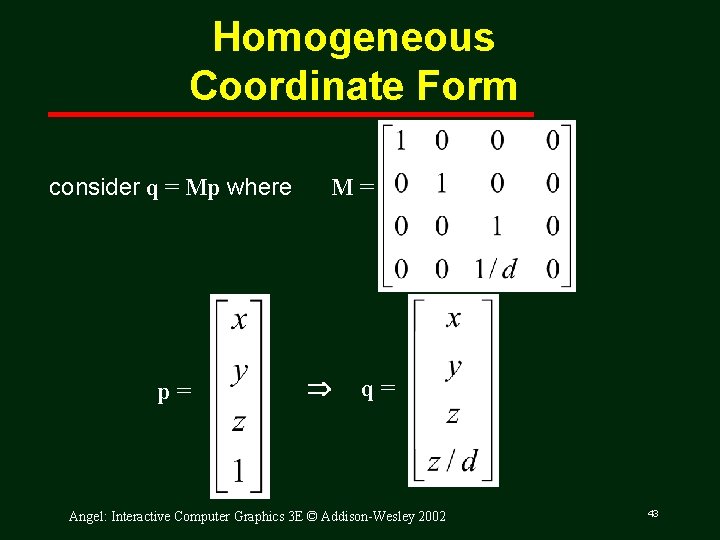
Homogeneous Coordinate Form consider q = Mp where p= M= q= Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 43

Perspective Division • However w 1, so we must divide by w to return from homogeneous coordinates • This perspective division yields xp = yp = zp = d = the desired perspective equations • We will consider the corresponding clipping volume with the Open. GL functions Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 44

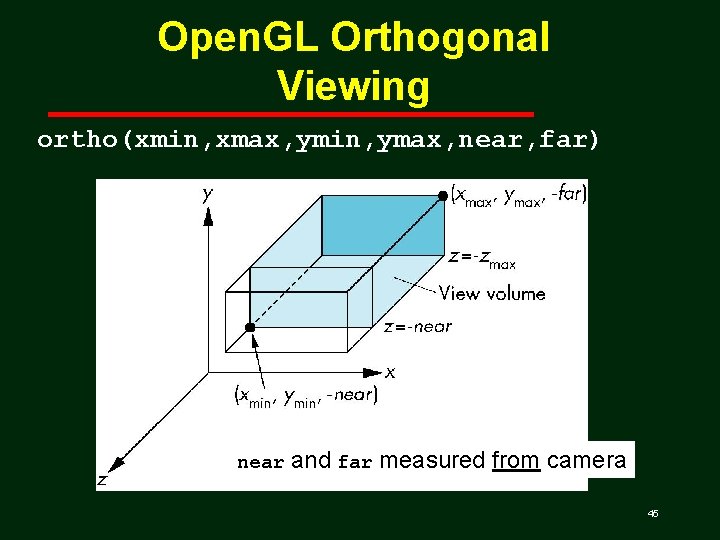
Open. GL Orthogonal Viewing ortho(xmin, xmax, ymin, ymax, near, far) near and far measured from camera 45

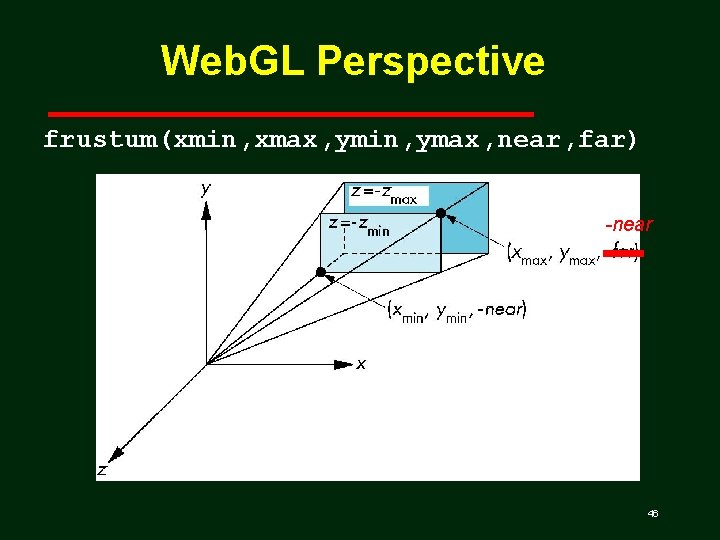
Web. GL Perspective frustum(xmin, xmax, ymin, ymax, near, far) -near 46

Using Field of View • With frustum it is often difficult to get the desired view • perpective(fovy, aspect, near, far) often provides a better interface front plane aspect = w/h Angel and Shreiner: Interactive Computer Graphics 7 E © Addison-Wesley 2015 47

Now, we will look at how the Open. GL projection matrices are computed…

Normalization • Rather than derive a different projection matrix for each type of projection, we can convert all projections to orthogonal projections with the default view volume • This strategy allows us to use standard transformations in the pipeline and makes for efficient clipping Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 49

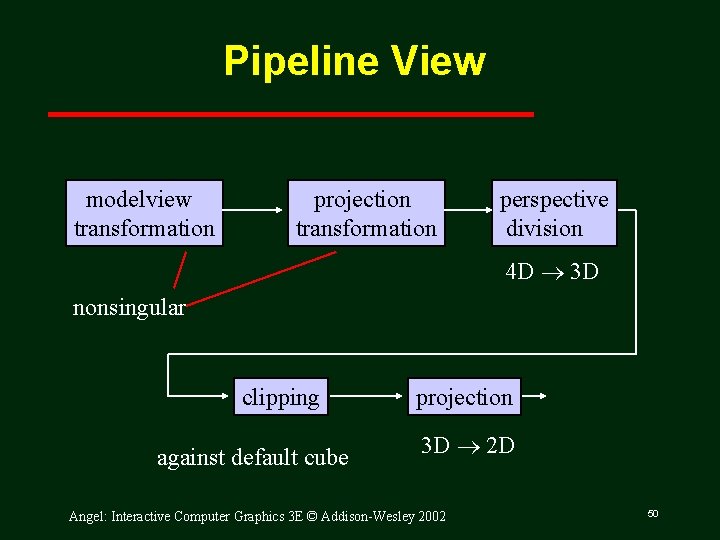
Pipeline View modelview transformation projection transformation perspective division 4 D 3 D nonsingular clipping against default cube projection 3 D 2 D Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 50

Notes • We stay in four dimensional homogeneous coordinates through both the modelview and projection transformations Both these transformations are nonsingular Default to identity matrices (orthogonal view) • Normalization lets us clip against simple cube regardless of type of projection • Delay final projection until end Important for hidden surface removal to retain depth information as long as possible Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 51

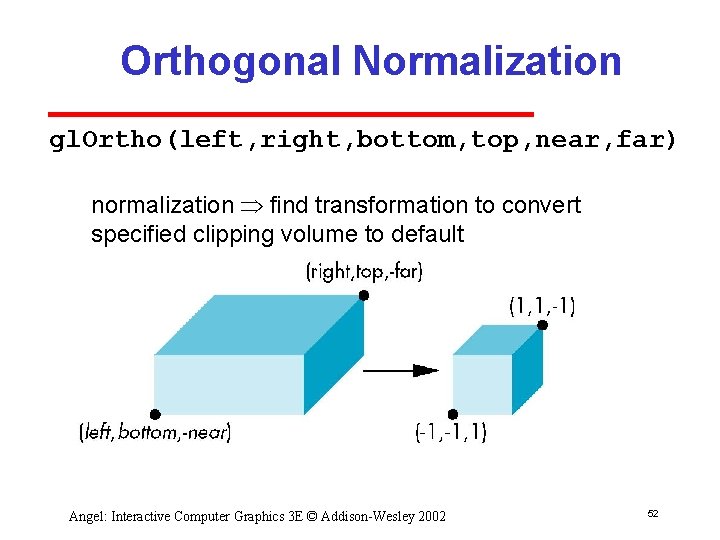
Orthogonal Normalization gl. Ortho(left, right, bottom, top, near, far) normalization find transformation to convert specified clipping volume to default Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 52

Orthogonal Matrix • Two steps Move center to origin T(-(left+right)/2, -(bottom+top)/2, (near+far)/2)) Scale to have sides of length 2 S(2/(left-right), 2/(top-bottom), 2/(near-far)) P = ST = Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 53

Final Projection • Set z =0 • Equivalent to the homogeneous coordinate transformation Morth = • Hence, general orthogonal projection in 4 D is P = Morth. ST Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 54

Perspective in Open. GL • gl. Frustum( left, right, bottom, top, near, far ) • glu. Perpective( FOV_vertical, aspect_ratio, near, far ) Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 55

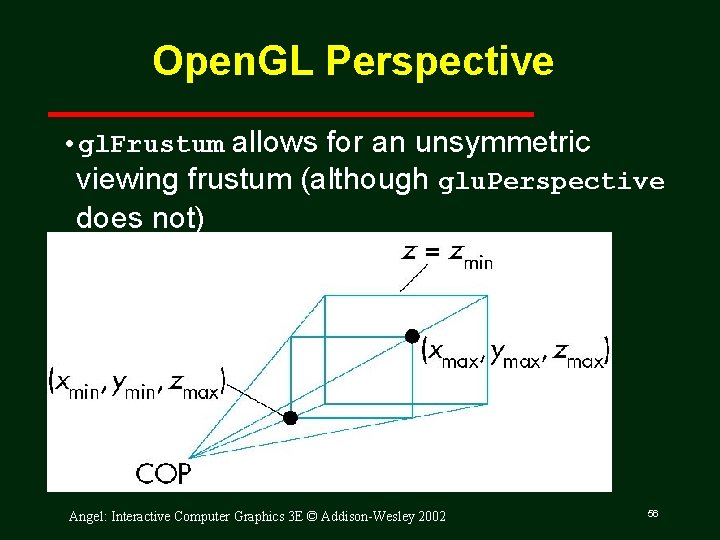
Open. GL Perspective • gl. Frustum allows for an unsymmetric viewing frustum (although glu. Perspective does not) Angel: Interactive Computer Graphics 3 E © Addison-Wesley 2002 56

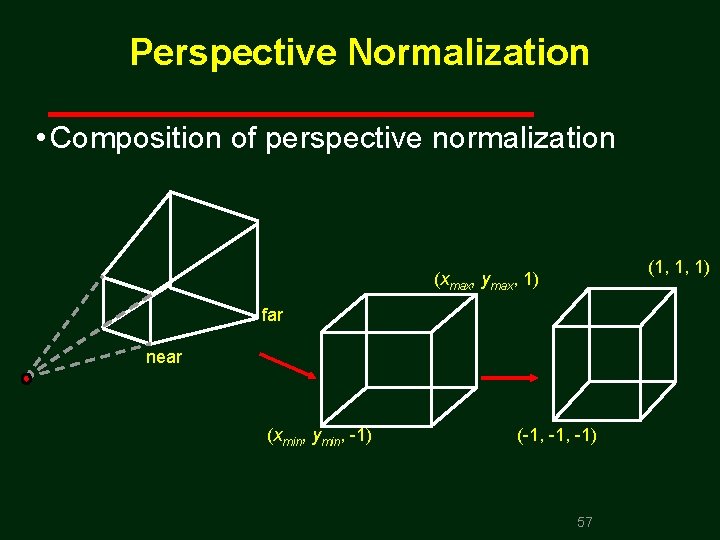
Perspective Normalization • Composition of perspective normalization (1, 1, 1) (xmax, ymax, 1) far near (xmin, ymin, 1) ( 1, 1) 57

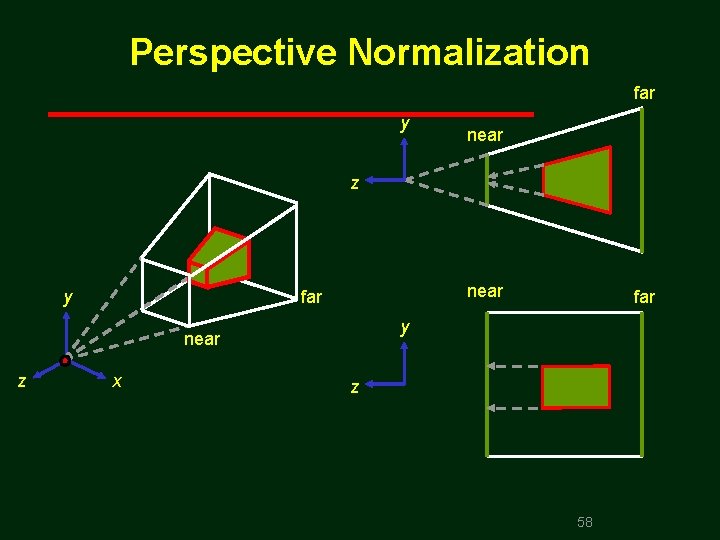
Perspective Normalization far y near z y near far y near z x far z 58

Why do we do it this way? • Normalization allows for a single pipeline for both perspective and orthogonal viewing • We keep in four dimensional homogeneous coordinates as long as possible to retain three dimensional information needed for hidden surface removal and shading • We simplify clipping 59

Generalization N= after persepective divison, the point (x, y, z, 1) goes to x’’ = x/z y’’ = y/z z’’ = -(a+b/z) which projects orthogonally to the desired point regardless of a and b 60

Picking a and b If we pick a= b= the near plane is mapped to z = -1 the far plane is mapped to z =1 and the sides are mapped to x = 1, y = 1 Hence the new clipping volume is the default clipping volume 61

Now let’s look at the Z more carefully… 62

Normalization and Hidden -Surface Removal • Although our selection of the form of the perspective matrices may appear somewhat arbitrary, it was chosen so that if z 1 > z 2 in the original clipping volume then the z’s for the transformed points z 1’ > z 2’ • Thus hidden surface removal works if we first apply the normalization transformation • However, the formula z’’ = -(a+b/z) implies that the distances are distorted by the normalization which can cause numerical problems especially if the near distance is small 63

The Z Component • So far, we have ignored the Z coordinate. • We want to convert Z so that the range of [near, far] becomes [ 1, 1] • Note that this is NOT a “uniform” scaling. We will see why after a few slides. 64

Range of Z • If Z = near, what is Z’? 1 • If Z = far, what is Z’? 1 • Does Z’ change linearly with Z? No! Let a= b= Z’ = Zw / w = (a*Z+b) / Z = a + b/Z 65

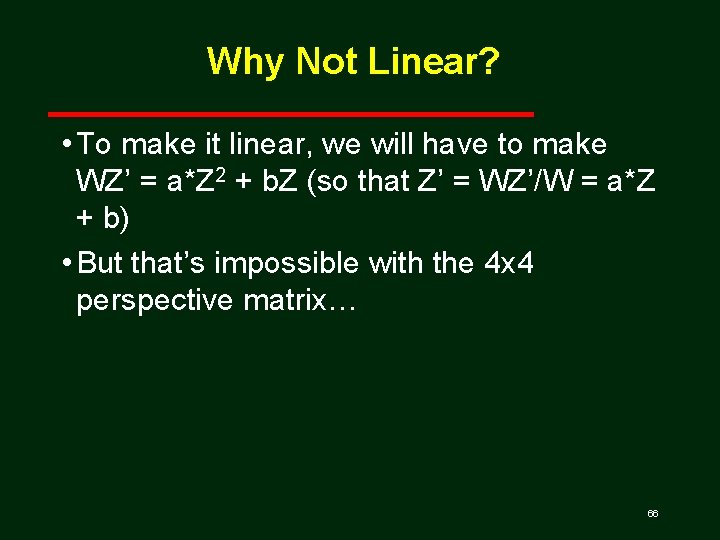
Why Not Linear? • To make it linear, we will have to make WZ’ = a*Z 2 + b. Z (so that Z’ = WZ’/W = a*Z + b) • But that’s impossible with the 4 x 4 perspective matrix… 66

Z Resolution • Since screen Z’ is expressed in the form of a+b/Z, most of the Z resolution is used up by the Z’s closer to the near plane. • So, what does this mean? • You should NOT set z. Near to be very close to the eye position. 67

68

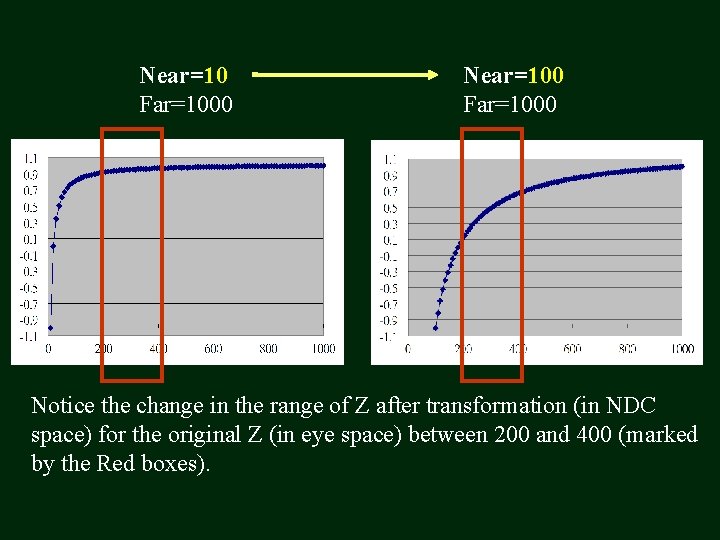
Near=10 Far=1000 Near=100 Far=1000 Notice the change in the range of Z after transformation (in NDC space) for the original Z (in eye space) between 200 and 400 (marked by the Red boxes).

Now, some more math… 70

Transformation of Normals • Transformation does not necessarily preserve the normal vectors. If a. b=0, does T(a). T(b)=0 also? • For example: what happen if we scale (X, Y) by (0. 5, 1. 0) in a 2 D image? 71

We shouldn’t transform the two end points of a normal vector. What we should do is to transform (three points of) the plane first, then find its normal. What does that mean in math? (See Appendix F of the Open. GL red book. ) 72

Transformation of Normals • (Foley/van. Dam pages 216 217) NT. P = 0 but is (MN)T. MP=0? Not always!! Let (QN)T. MP=0 (i. e. , transform P first, then try to find its normal) NTQTMP=0 So QTM=I QT= M 1 or Q=(M 1)T • Special case when M 1=MT If M consists of only the composition of rotation, translation, and uniform scaling. Q=M 73