Viewing in 3 D 3 D worldcoordinate output

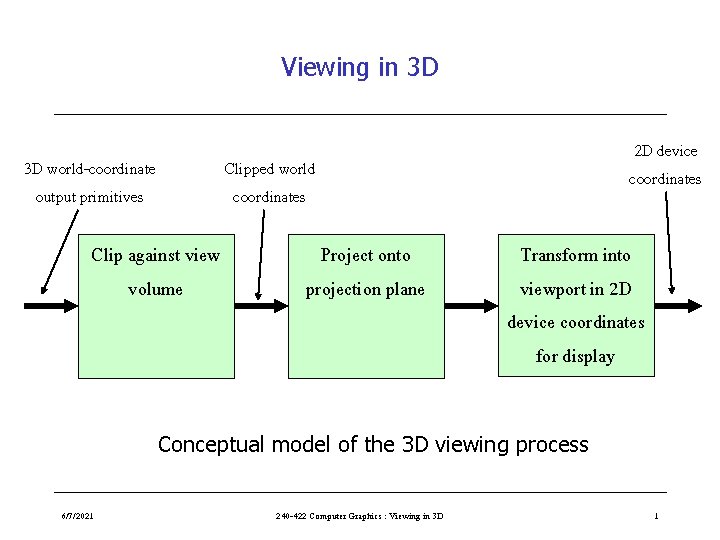
Viewing in 3 D 3 D world-coordinate output primitives 2 D device coordinates Clipped world coordinates Clip against view volume Project onto projection plane Transform into viewport in 2 D device coordinates for display Conceptual model of the 3 D viewing process 6/7/2021 240 -422 Computer Graphics : Viewing in 3 D 1

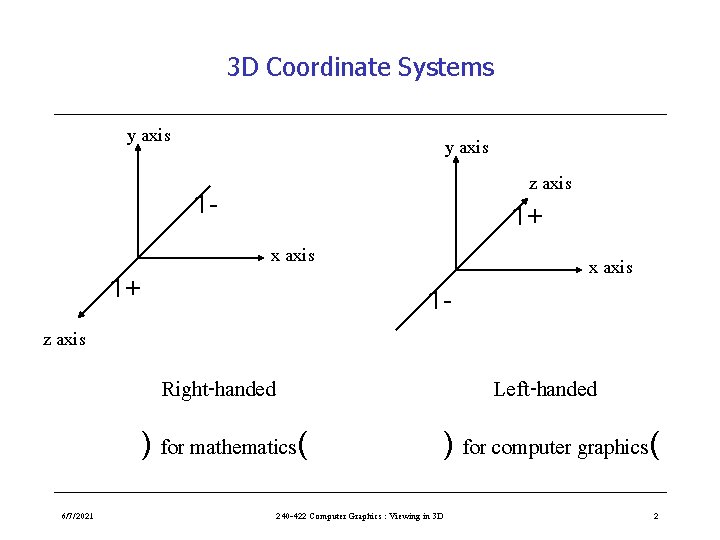
3 D Coordinate Systems y axis 1 - 1+ x axis 1 - z axis 1+ x axis z axis 6/7/2021 Right-handed Left-handed ) for mathematics( ) for computer graphics( 240 -422 Computer Graphics : Viewing in 3 D 2

3 D Primitives: Point & Line • Any point in 3 D coordinate is defined by (x, y, z( • Any line in 3 D coordinate is defined with 2 points: )x 1, y 1, z 1) and (x 2, y 2, z 2( • Line equations: or 6/7/2021 240 -422 Computer Graphics : Viewing in 3 D 3

3 D Primitives: Planes • A plane is specified as Ax + By + Cz + D = 0 or (A, B, C, D are constants( x + B 1 y + C 1 z + D 1 = 0 )where B 1 = B/A, C 1 = C/A and D 1 = D/A( • If we know 3 points (not all in a line), we can determine the plain equation from x 1 + B 1 y 1 + C 1 z 1 + D 1 = 0 x 2 + B 1 y 2 + C 1 z 2 + D 1 = 0 x 3 + B 1 y 3 + C 1 z 3 + D 1 = 0 Solving for B 1, C 1, D 1 yields the plain equation 6/7/2021 240 -422 Computer Graphics : Viewing in 3 D 4

3 D Primitives: Planes (cont’d) • A plane can also be specified with a single point in the plane (xp, yp, zp) and the normal vector (direction perpendicular to the plane) [Nx, Ny, Nz[ ]Nx, Ny, Nz[ )xp, yp, zp( Plane equation: Nx(x-xp) + Ny(y-yp) +Nz(z-zp) = 0 6/7/2021 240 -422 Computer Graphics : Viewing in 3 D 5

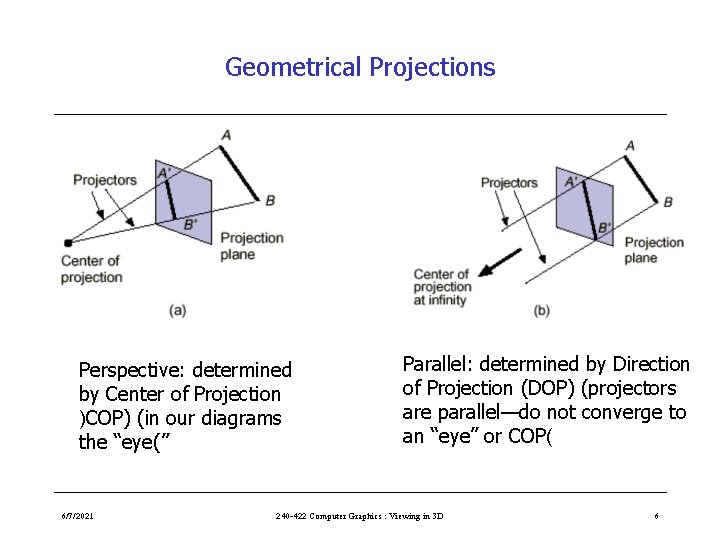
Geometrical Projections Perspective: determined by Center of Projection )COP) (in our diagrams the “eye(” 6/7/2021 Parallel: determined by Direction of Projection (DOP) (projectors are parallel—do not converge to an “eye” or COP( 240 -422 Computer Graphics : Viewing in 3 D 6

Parallel Projection • Suppose the direction of projection is given by the vector [xp, yp, zp] and the image is to be projected onto the xy plane • If we have a point on the object at (x 1, y 1, z 1), we wish to determine where the projected point (x 2, y 2) will lie. • Writing the equations for a line passing the point (x, y, z) and in the direction of projection: x = x 1 + xp u y = y 1 + yp u z = z 1 + zp u 6/7/2021 240 -422 Computer Graphics : Viewing in 3 D 7

Parallel Projection • Where does this line intersect the xy plane (z=0? ( Since u = -z 1/zp substituting this into the first two equations gives x 2 = x 1 - z 1 (xp/zp( y 2 = y 1 - z 1 (yp/zp( This can be written in matrix form 6/7/2021 240 -422 Computer Graphics : Viewing in 3 D 8

Perspective Projection • The further an object is from the viewer, the smaller it appears • If the center of projection is at (xc, yc, zc) and the point on the object is (x 1, y 1, z 1) then the project ray will be the line containing these points and will be given by x = xc + (x 1 -xc)u y = yc + (y 1 -yc)u z = zc + (z 1 -zc)u 6/7/2021 240 -422 Computer Graphics : Viewing in 3 D 9

Perspective Projection • The projected point (x 2, y 2) will be the point where this line intersects the xy plane • For this intersection point (z=0), we can compute u u = -zc / (z 1 -zc( • Substituting into the first two equations gives or 6/7/2021 240 -422 Computer Graphics : Viewing in 3 D 10

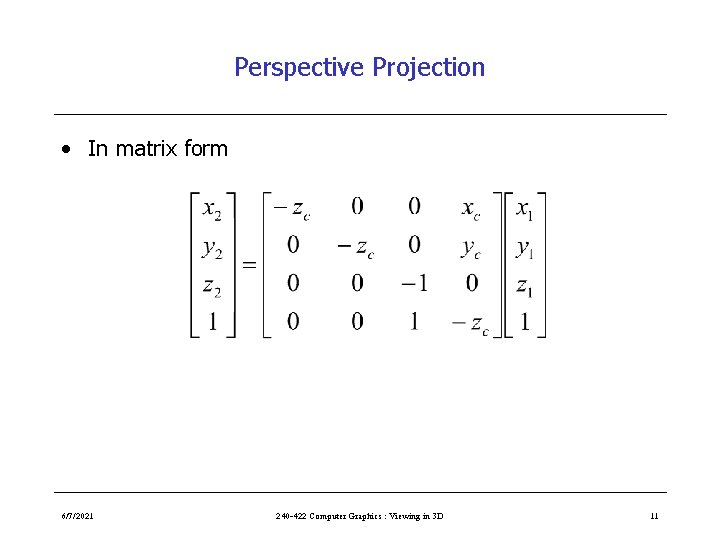
Perspective Projection • In matrix form 6/7/2021 240 -422 Computer Graphics : Viewing in 3 D 11