Viewing and Projection Parallel Projection Parallel Projections known

Viewing and Projection

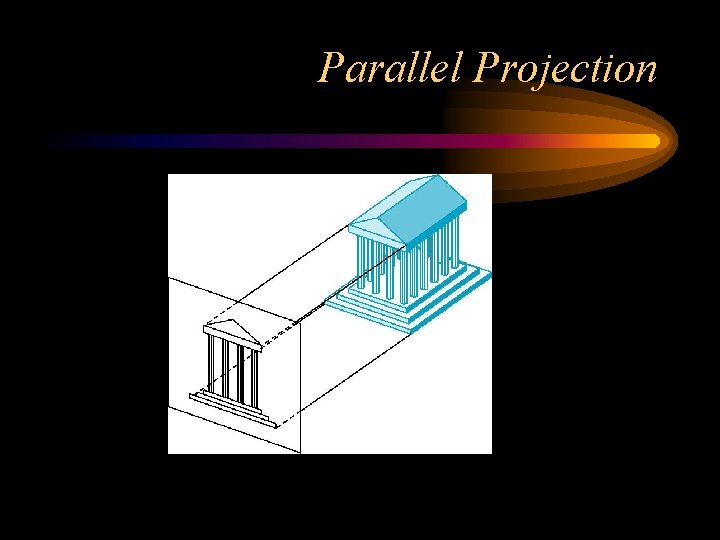
Parallel Projection

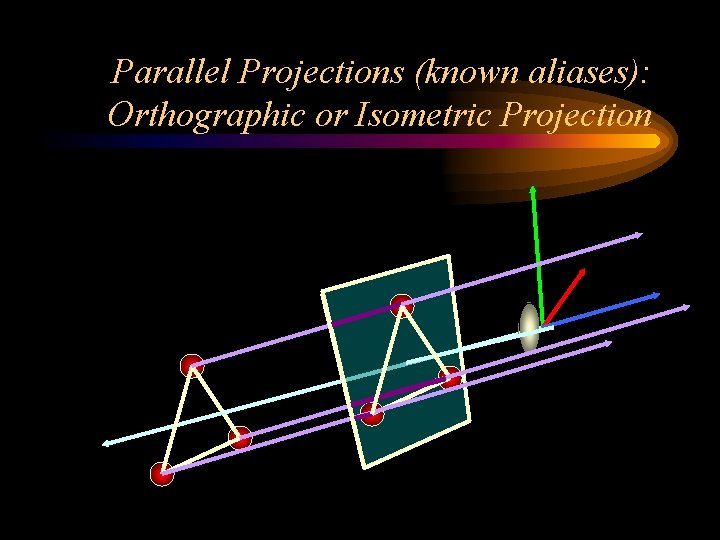
Parallel Projections (known aliases): Orthographic or Isometric Projection

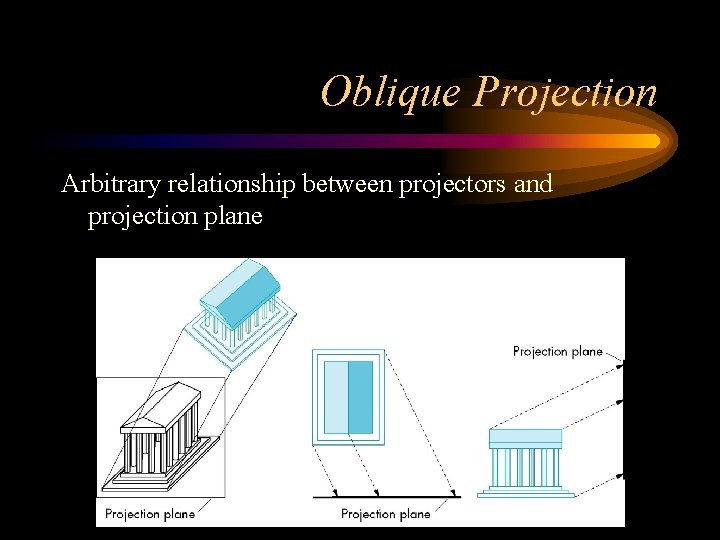
Oblique Projection Arbitrary relationship between projectors and projection plane 4 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

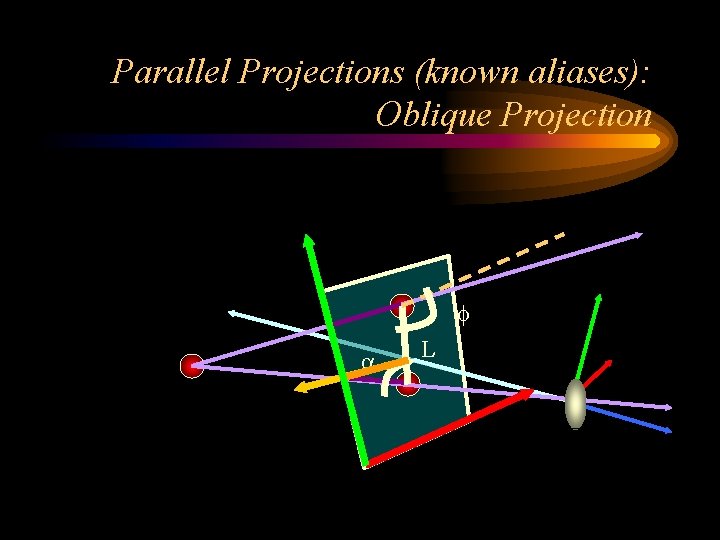
Parallel Projections (known aliases): Oblique Projection L

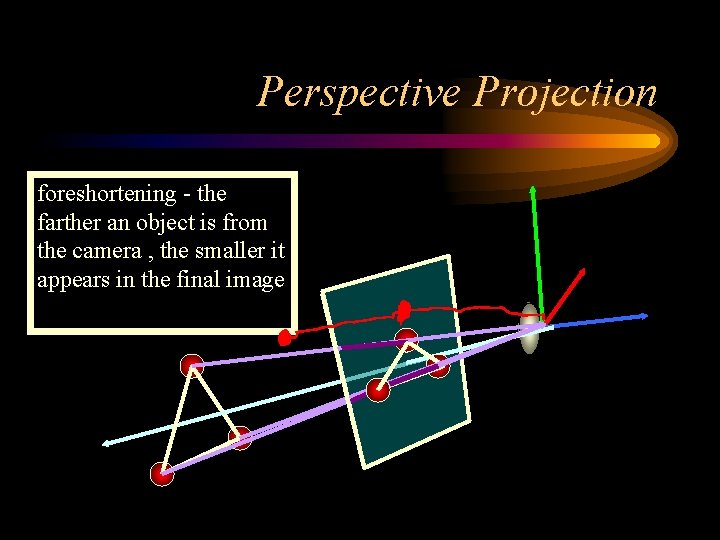
Perspective Projection Projectors coverge at center of projection 6 Angel: Interactive Computer Graphics 5 E © Addison-Wesley 2009

Perspective Projection foreshortening - the farther an object is from the camera , the smaller it appears in the final image

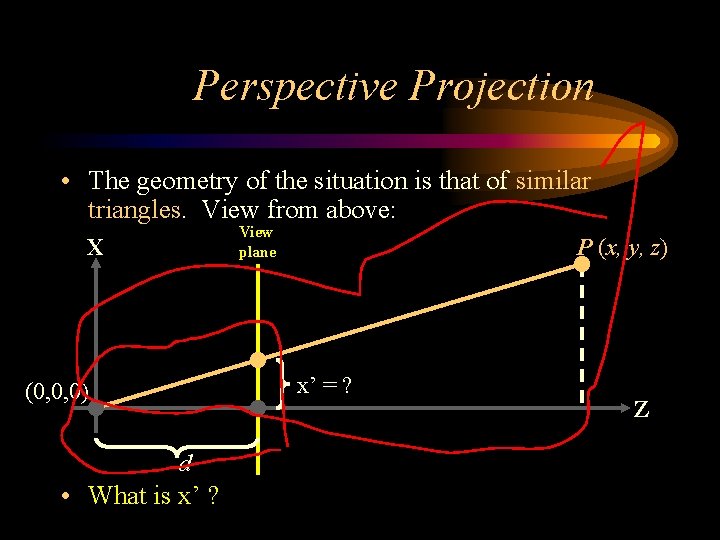
Perspective Projection • The geometry of the situation is that of similar triangles. View from above: View plane X P (x, y, z) x’ = ? (0, 0, 0) d • What is x’ ? Z

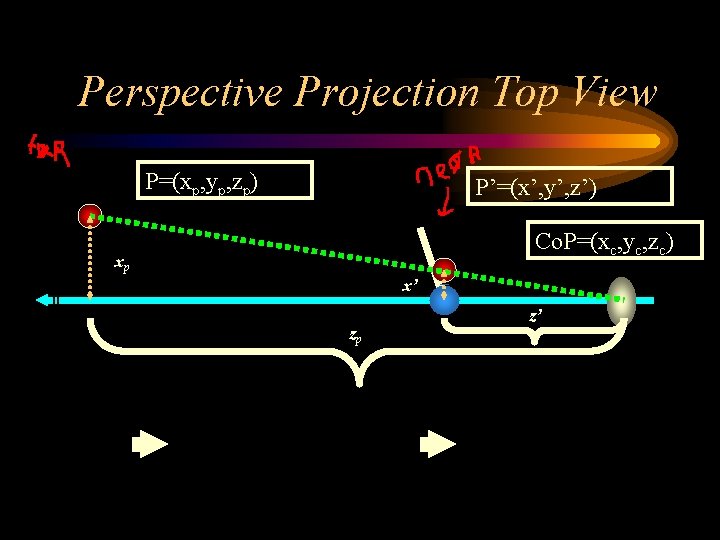
Perspective Projection Top View P=(xp, yp, zp) P’=(x’, y’, z’) Co. P=(xc, yc, zc) xp x’ zp z’

Simple Perspective Consider a simple perspective with the COP at the origin, the near clipping plane at z = -1, and a 90 degree field of view determined by the planes x = z, y = z 10 Angel: Interactive Computer Graphics 5 © Addison-Wesley 2009

Perspective Matrices Simple projection matrix in homogeneous coordinates M= Note that this matrix is independent of the far clipping plane 11 Angel: Interactive Computer Graphics 5 © Addison-Wesley 2009

Generalization N= after perspective division, the point (x, y, z, 1) goes to x’’ = x/z y’’ = y/z Z’’ = -( +b/z) which projects orthogonally to the desired point regardless of and b 12 Angel: Interactive Computer Graphics 5 © Addison-Wesley 2009

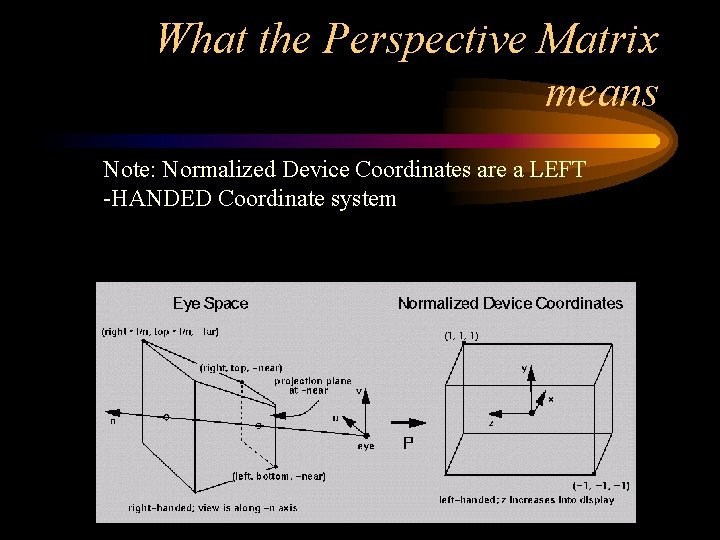
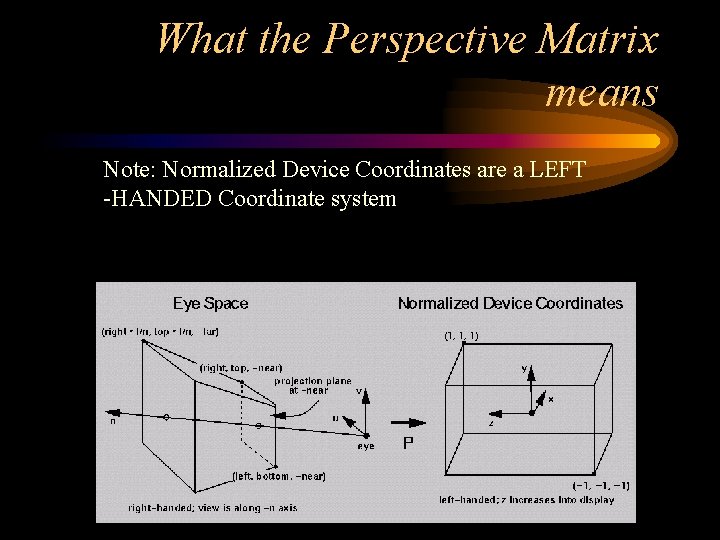
What the Perspective Matrix means Note: Normalized Device Coordinates are a LEFT -HANDED Coordinate system

Picking a and b If we pick = b= the near plane is mapped to z = -1 the far plane is mapped to z =1 and the sides are mapped to x = 1, y = 1 Hence the new clipping volume is the default clipping volume 14 Angel: Interactive Computer Graphics 5 © Addison-Wesley 2009

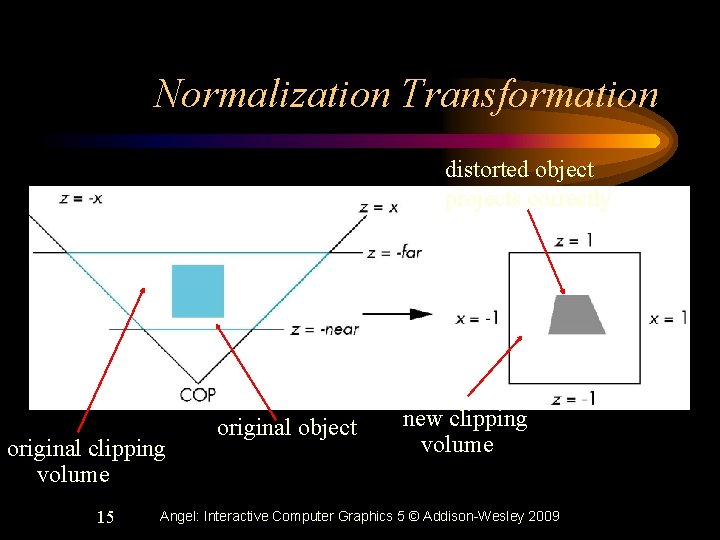
Normalization Transformation distorted object projects correctly original clipping volume 15 original object new clipping volume Angel: Interactive Computer Graphics 5 © Addison-Wesley 2009

Open. GL Perspective • gl. Frustum allows for an unsymmetric viewing frustum (although glu. Perspective does not) 16 Angel: Interactive Computer Graphics 5 © Addison-Wesley 2009

Open. GL Perspective Matrix • The normalization in gl. Frustum requires an initial shear to form a right viewing pyramid, followed by a scaling to get the normalized perspective volume. Finally, the perspective matrix results in needing only a final orthogonal transformation P = NSH our previously defined shear and scale perspective matrix 17 Angel: Interactive Computer Graphics 5 © Addison-Wesley 2009

gl. Frustum Matrix

Why do we do it this way? • Normalization allows for a single pipeline for both perspective and orthogonal viewing • We stay in four dimensional homogeneous coordinates as long as possible to retain three-dimensional information needed for hidden-surface removal and shading • We simplify clipping 19 Angel: Interactive Computer Graphics 5 © Addison-Wesley 2009

What the Perspective Matrix means Note: Normalized Device Coordinates are a LEFT -HANDED Coordinate system

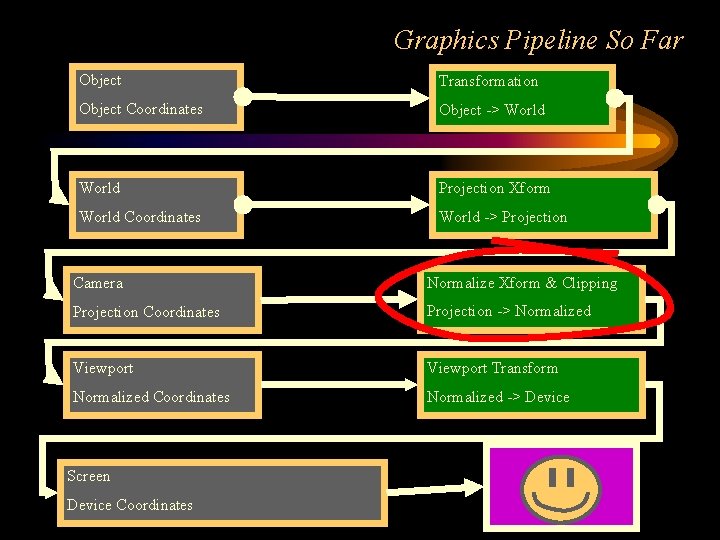
Graphics Pipeline So Far Object Transformation Object Coordinates Object -> World Projection Xform World Coordinates World -> Projection Camera Normalize Xform & Clipping Projection Coordinates Projection -> Normalized Viewport Transform Normalized Coordinates Normalized -> Device Screen Device Coordinates

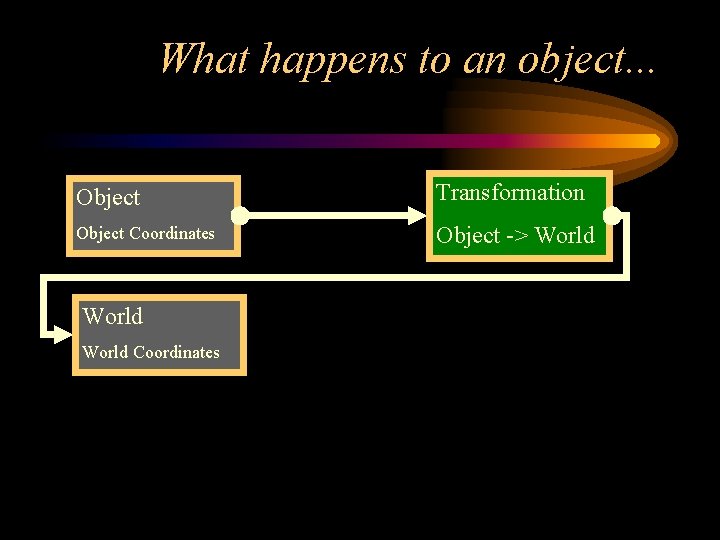
What happens to an object. . . Object Transformation Object Coordinates Object -> World Coordinates

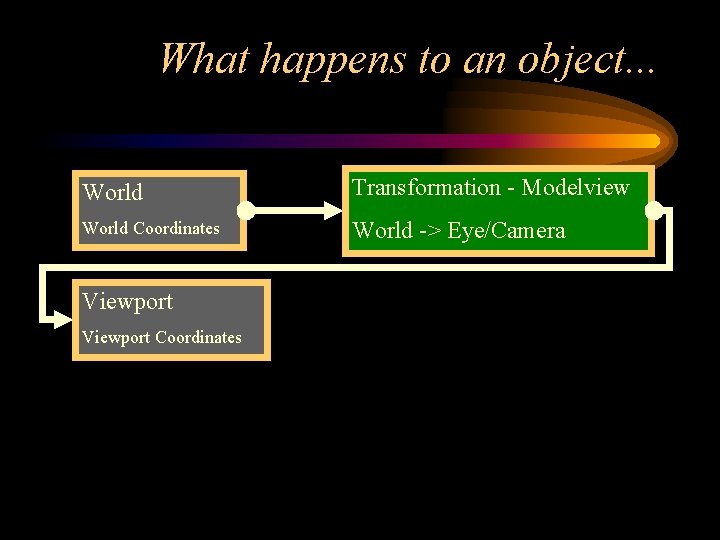
What happens to an object. . . World Transformation - Modelview World Coordinates World -> Eye/Camera Viewport Coordinates

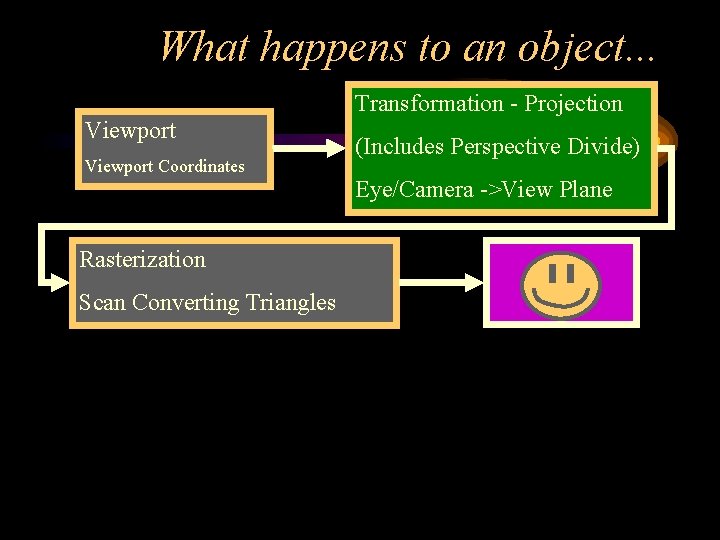
What happens to an object. . . Transformation - Projection Viewport Coordinates Rasterization Scan Converting Triangles (Includes Perspective Divide) Eye/Camera ->View Plane