Vibrations and Waves 1 SIMPLE HARMONIC MOTION Physical

Vibrations and Waves

1 SIMPLE HARMONIC MOTION • Physical Characteristics of Simple Harmonic Oscillators • A mass on a Spring • The Pendulum • Energy in the Simple Harmonic Oscillator • The Period and Sinusoidal Nature of SHM • Oscillations in Electrical Circuits: Similarities in Physics

SIMPLE HARMONIC MOTION • 1. 1 Physical Characteristics of Simple Harmonic Oscillators • 1. 2 A Mass on a Spring – – – 1. 2. 1 A mass on a horizontal spring 1. 2. 2 A mass on a vertical spring 1. 2. 3 Displacement, velocity and acceleration in simple harmonic motion 1. 2. 4 General solutions for simple harmonic motion and the phase angle φ 1. 2. 5 The energy of a simple harmonic oscillator 1. 2. 6 The physics of small vibrations • 1. 3 The Pendulum – – 1. 3. 1 The simple pendulum 1. 3. 2 The energy of a simple pendulum 1. 3. 3 The physical pendulum 1. 3. 4 Numerical solution of simple harmonic motion • 1. 4 Oscillations in Electrical Circuits: Similarities in Physics – 1. 4. 1 The LC circuit – 1. 4. 2 Similarities in physics • PROBLEMS 1

Oscillatory Motion which is periodic in time, that is, motion that repeats itself in time. Examples: • Power line oscillates when the wind blows past it • Earthquake oscillations move buildings

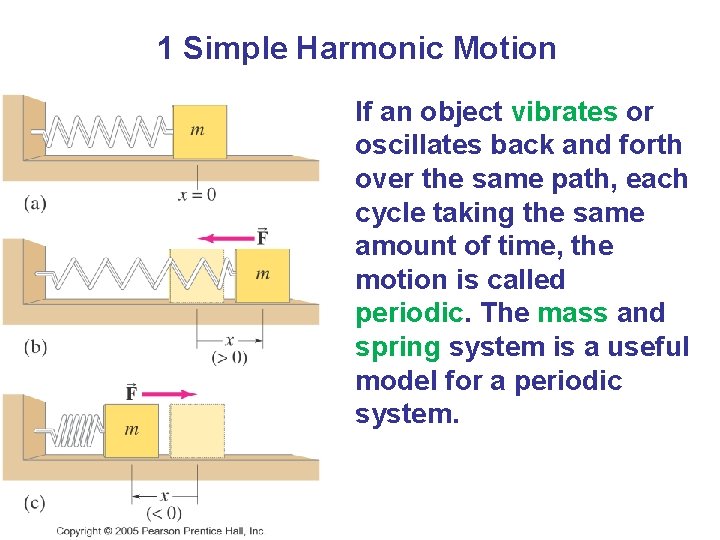
1 Simple Harmonic Motion If an object vibrates or oscillates back and forth over the same path, each cycle taking the same amount of time, the motion is called periodic. The mass and spring system is a useful model for a periodic system.

1 Simple Harmonic Motion We assume that the surface is frictionless. There is a point where the spring is neither stretched nor compressed; this is the equilibrium position. We measure displacement from that point (x = 0 on the previous figure). The force exerted by the spring depends on the displacement: (11 -1)

1 Simple Harmonic Motion • The minus sign on the force indicates that it is a restoring force – it is directed to restore the mass to its equilibrium position. • k is the spring constant • The force is not constant, so the acceleration is not constant either

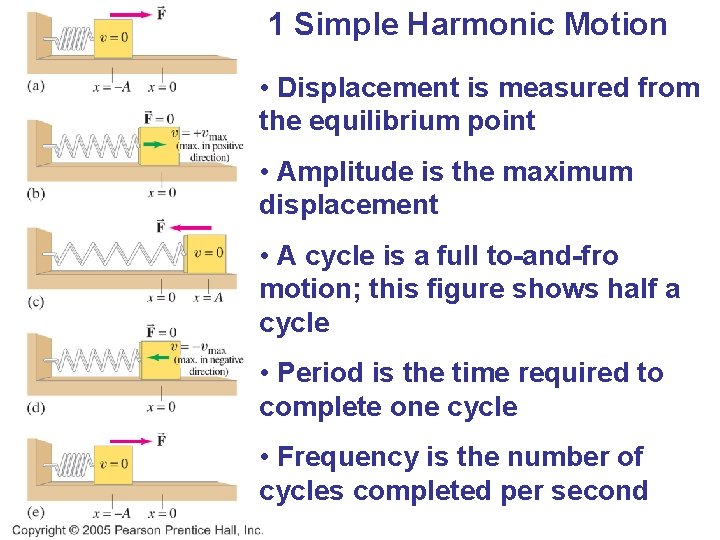
1 Simple Harmonic Motion • Displacement is measured from the equilibrium point • Amplitude is the maximum displacement • A cycle is a full to-and-fro motion; this figure shows half a cycle • Period is the time required to complete one cycle • Frequency is the number of cycles completed per second

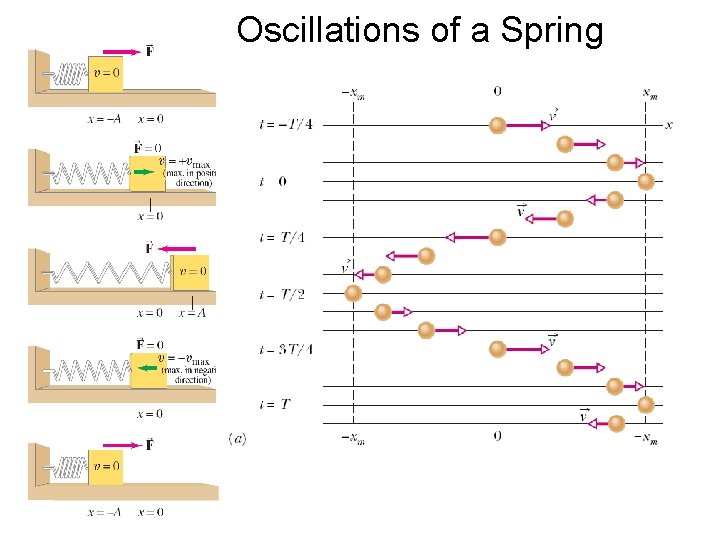
Oscillations of a Spring

Oscillations of a Spring • Displacement is measured from the equilibrium point. • Amplitude is the maximum displacement. • A cycle is a full to-and-fro motion. • Period is the time required to complete one cycle. • Frequency is the number of cycles completed per second.

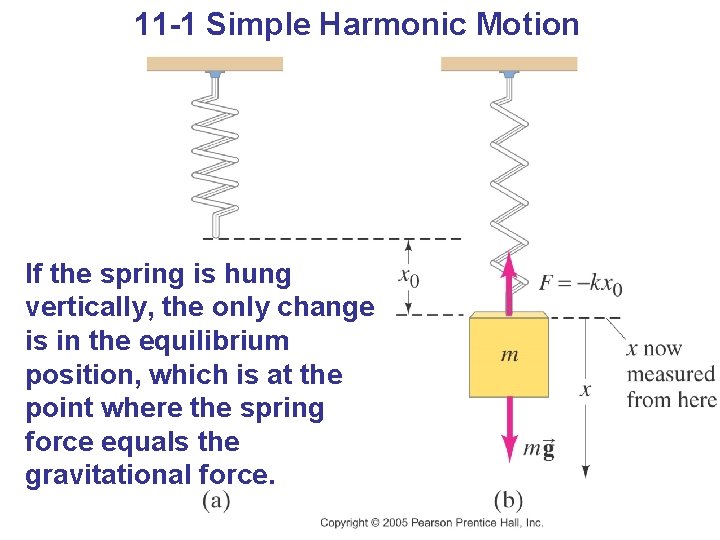
11 -1 Simple Harmonic Motion If the spring is hung vertically, the only change is in the equilibrium position, which is at the point where the spring force equals the gravitational force.

Oscillations of a Spring When a family of four with a total mass of 200 kg step into their 1200 -kg car, the car’s springs compress 3. 0 cm. (a) What is the spring constant of the car’s springs, assuming they act as a single spring? (b) How far will the car lower if loaded with 300 kg rather than 200 kg?

Solution:

Simple Harmonic Motion Substituting F = kx into Newton’s second law gives the equation of motion: with solutions of the form:

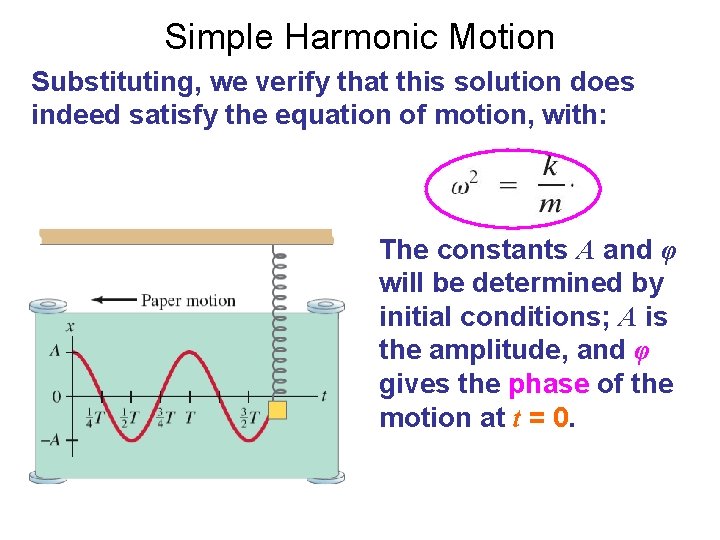
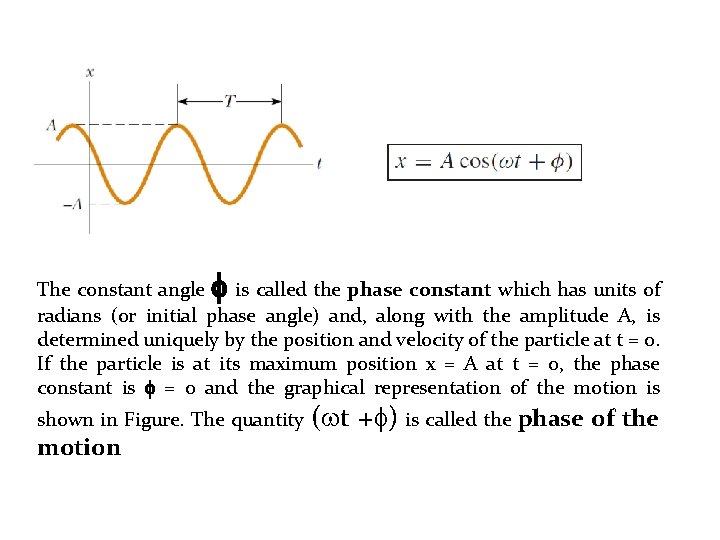
Simple Harmonic Motion Substituting, we verify that this solution does indeed satisfy the equation of motion, with: The constants A and φ will be determined by initial conditions; A is the amplitude, and φ gives the phase of the motion at t = 0.

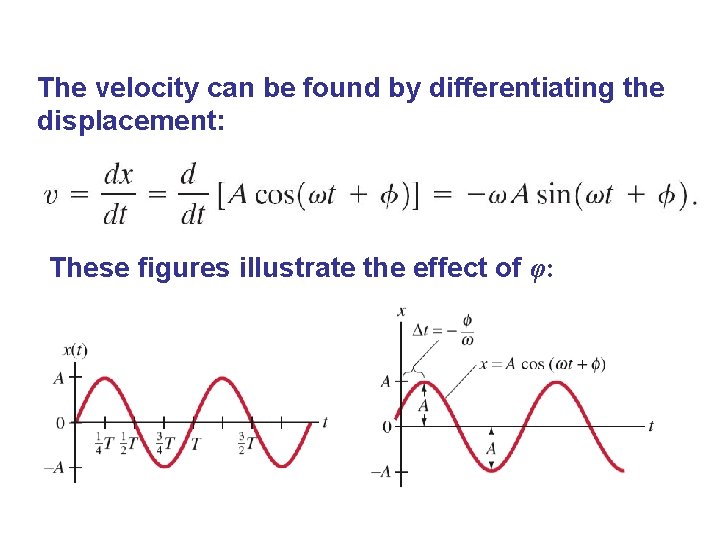
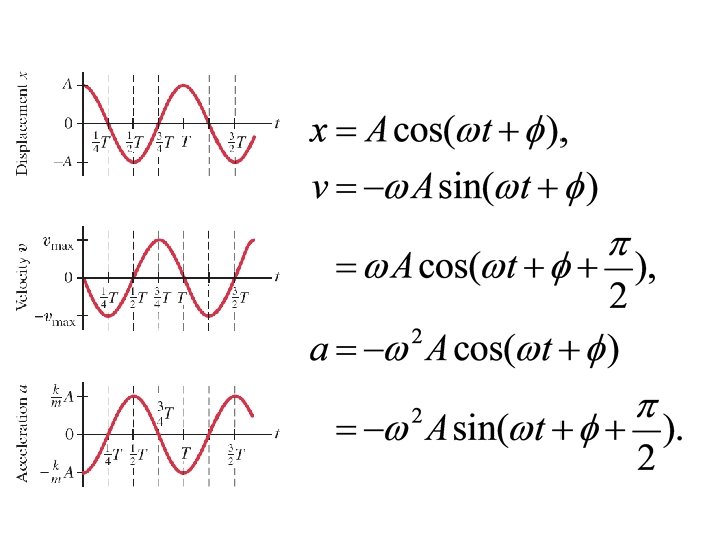
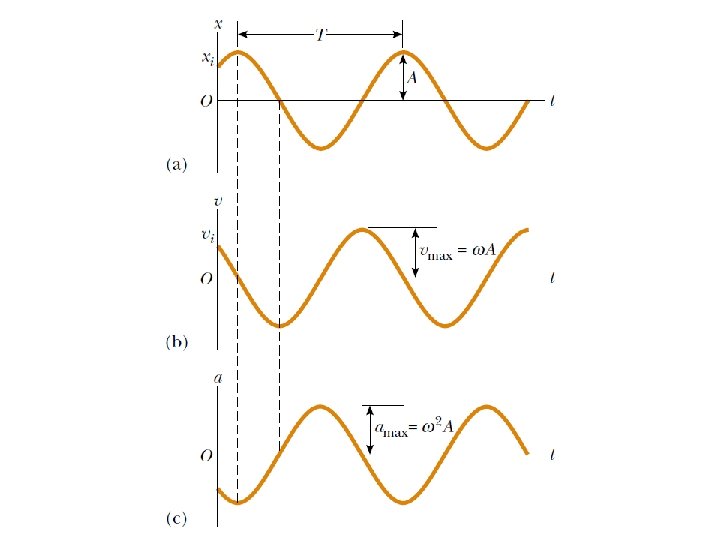
The velocity can be found by differentiating the displacement: These figures illustrate the effect of φ:

Simple Harmonic Motion Because then

Simple Harmonic Motion Determine the period and frequency of a car whose mass is 1400 kg and whose shock absorbers have a spring constant of 6. 5 x 104 N/m after hitting a bump. Assume the shock absorbers are poor, so the car really oscillates up and down.

Solution:

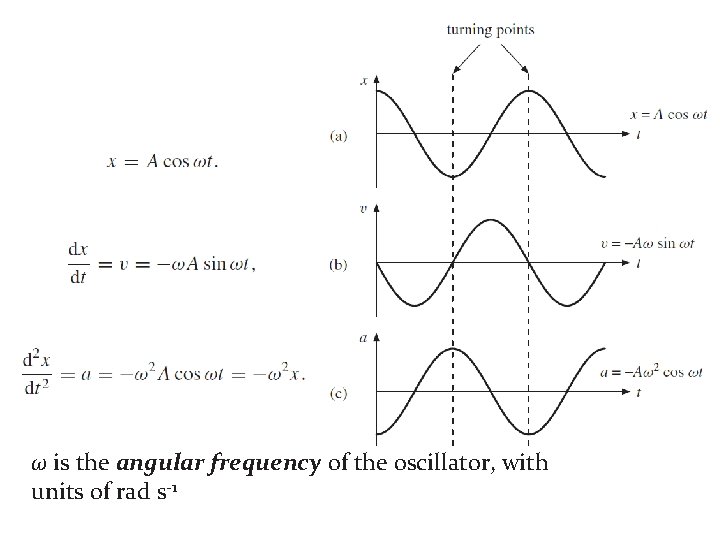
ω is the angular frequency of the oscillator, with units of rad s-1

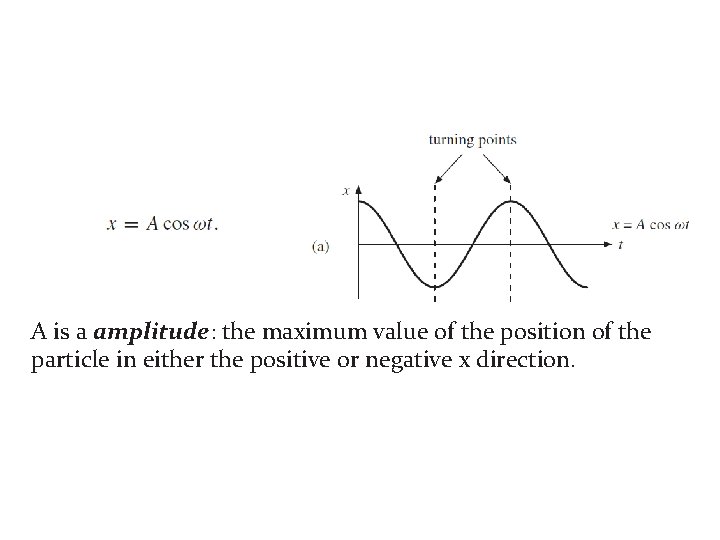
A is a amplitude: the maximum value of the position of the particle in either the positive or negative x direction.

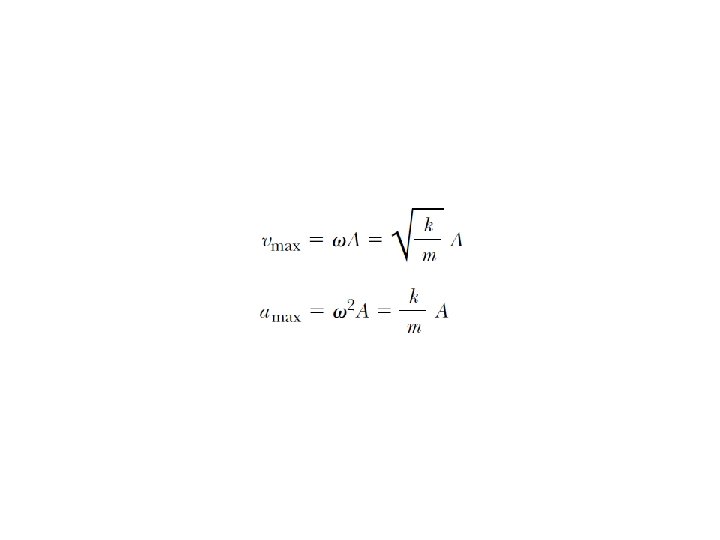
Simple Harmonic Motion A vibrating floor. A large motor in a factory causes the floor to vibrate at a frequency of 10 Hz. The amplitude of the floor’s motion near the motor is about 3. 0 mm. Estimate the maximum acceleration of the floor near the motor.

Solution: Assuming the motion is simple harmonic,

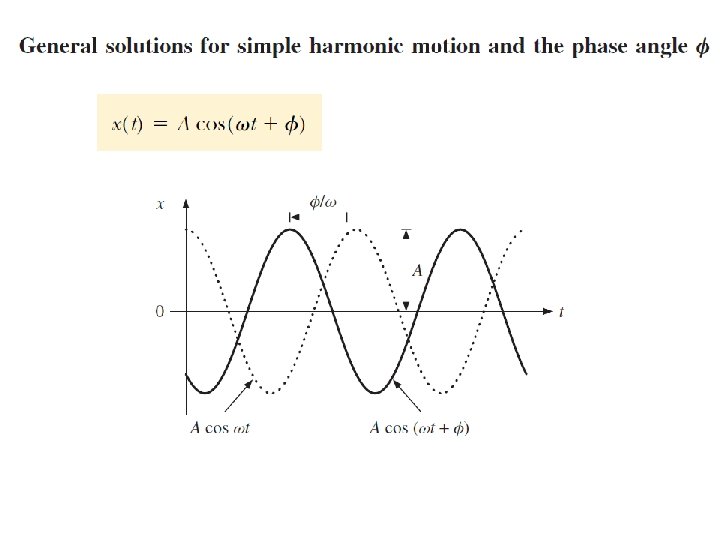
The constant angle is called the phase constant which has units of radians (or initial phase angle) and, along with the amplitude A, is determined uniquely by the position and velocity of the particle at t = 0. If the particle is at its maximum position x = A at t = 0, the phase constant is = 0 and the graphical representation of the motion is shown in Figure. The quantity motion ( t + ) is called the phase of the

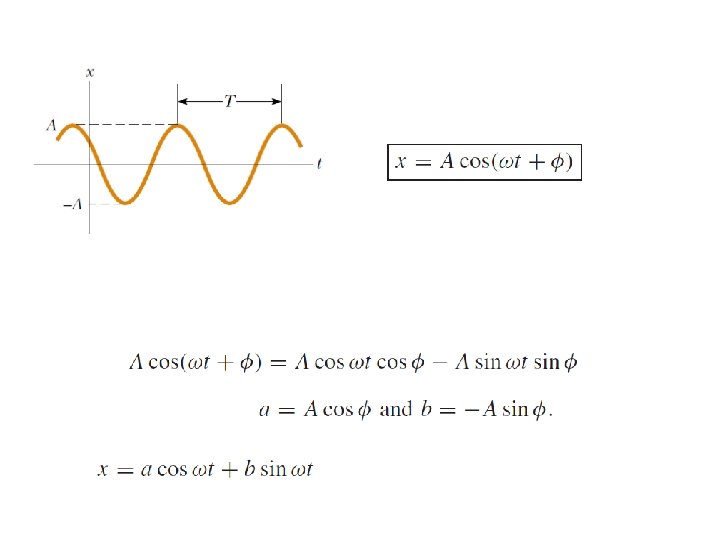
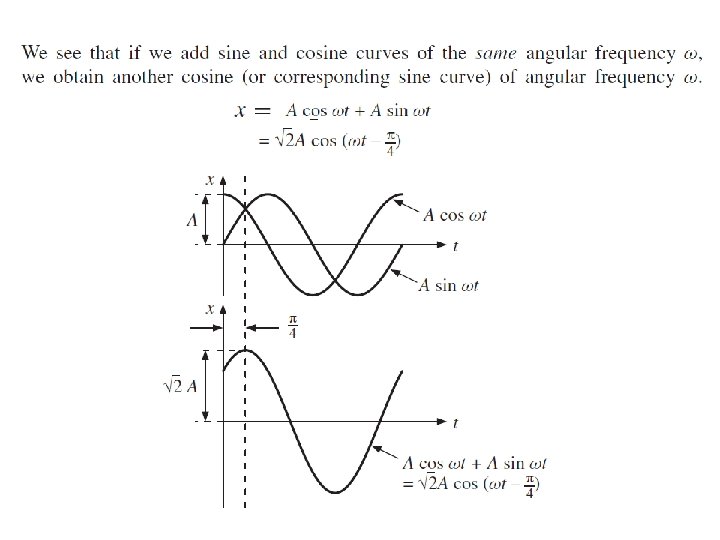
1 Simple Harmonic Motion Any vibrating system where the restoring force is proportional to the negative of the displacement is in simple harmonic motion (SHM), and is often called a simple harmonic oscillator.

An object oscillates with simple harmonic motion along the x axis. Its position varies with time according to the equation where t is in seconds and the angles in the parentheses are in radians. (A) Determine the amplitude, frequency, and period of the motion. (B) Calculate the velocity and acceleration of the object at any time t. (C) Using the results of part (B), determine the position, velocity, and acceleration of the object at t = 1. 00 s. (D) Determine the maximum speed and maximum acceleration of the object (E) Find the displacement of the object between t =0 and t =1. 00 s.

Spring calculations. A spring stretches 0. 150 m when a 0. 300 -kg mass is gently attached to it. The spring is then set up horizontally with the 0. 300 -kg mass resting on a frictionless table. The mass is pushed so that the spring is compressed 0. 100 m from the equilibrium point, and released from rest. Determine: (a) the spring stiffness constant k and angular frequency ω; (b) the amplitude of the horizontal oscillation A; (c) the magnitude of the maximum velocity vmax; (d) the magnitude of the maximum acceleration amax of the mass; (e) the period T and frequency f; (f) the displacement x as a function of time; and (g) the velocity at t = 0. 150 s.

Solution:

Spring is started with a push. Suppose the spring of the former example (where ω = 8. 08 s-1) is compressed 0. 100 m from equilibrium (x 0 = -0. 100 m) but is given a shove to create a velocity in the +x direction of v 0 = 0. 400 m/s. Determine (a) the phase angle φ, (b) the amplitude A, and (c) the displacement x as a function of time, x(t).

Solution:

1. 2. 5 The energy of a simple harmonic oscillator

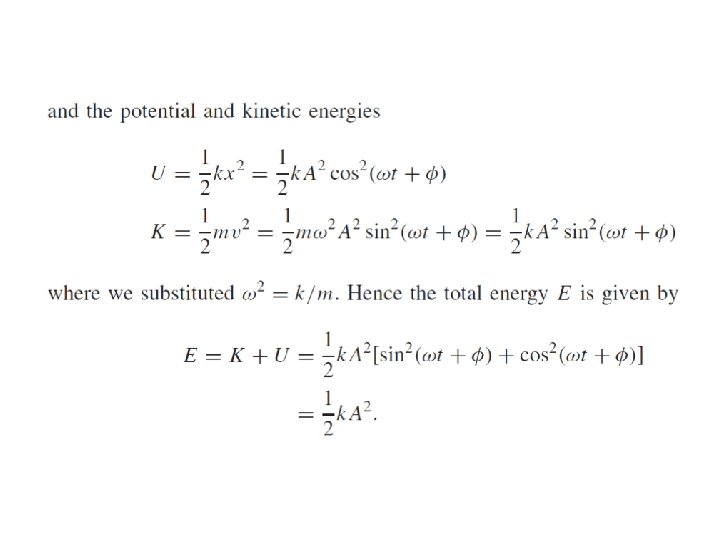
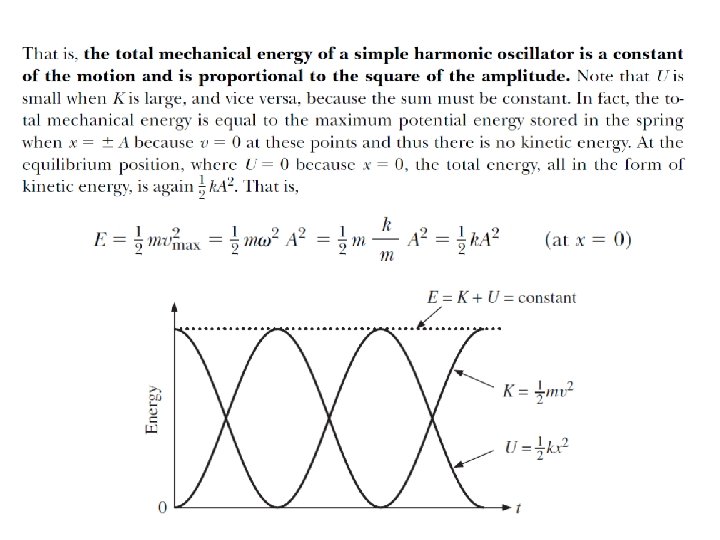
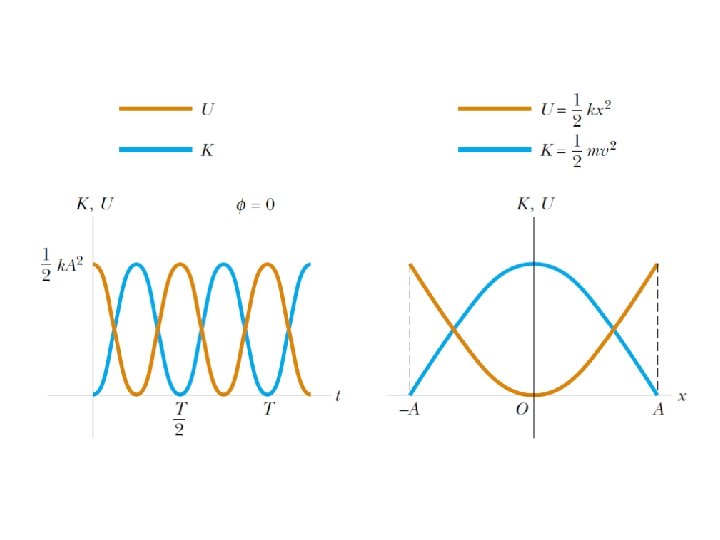
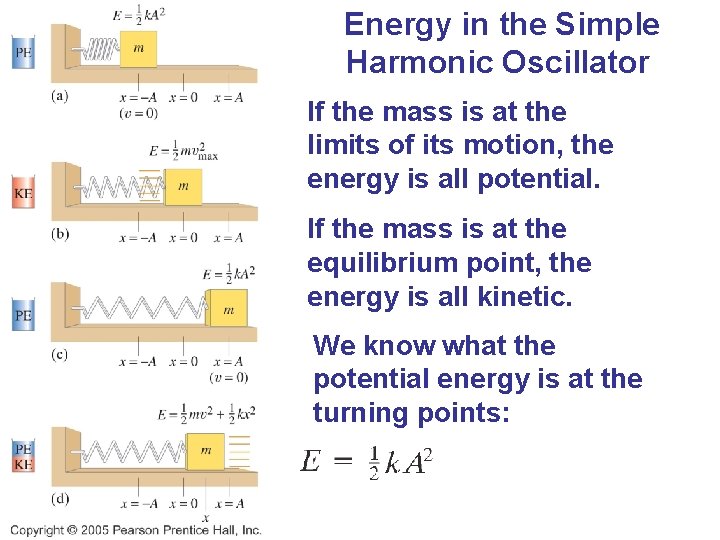
Energy in the Simple Harmonic Oscillator If the mass is at the limits of its motion, the energy is all potential. If the mass is at the equilibrium point, the energy is all kinetic. We know what the potential energy is at the turning points:

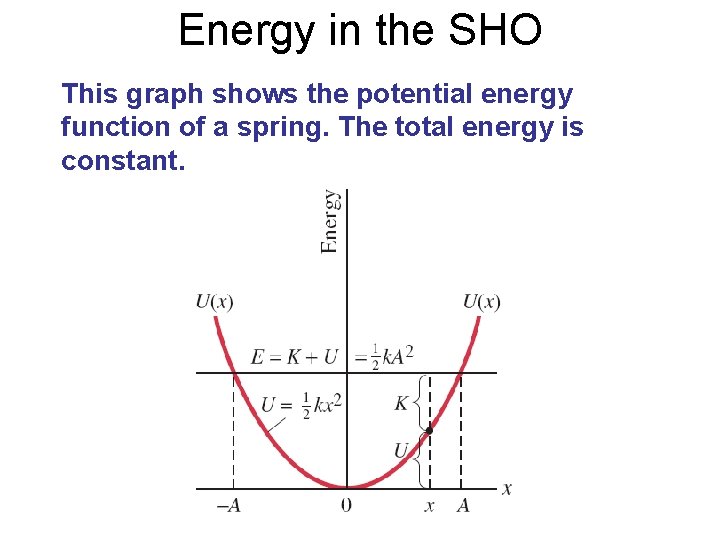
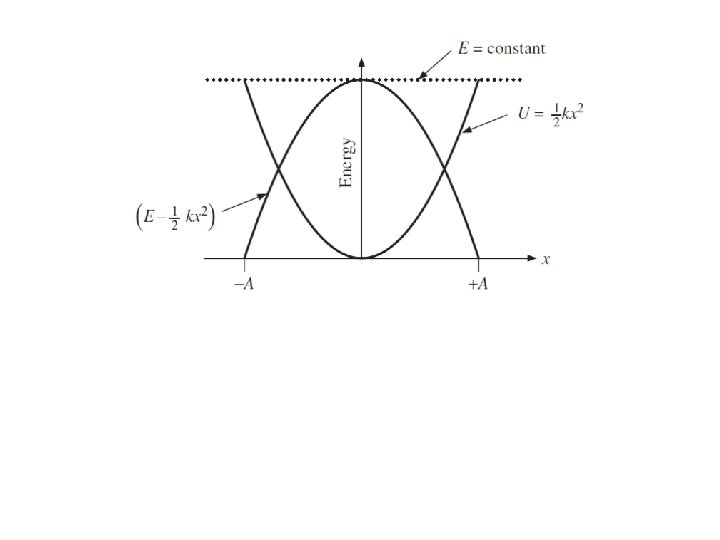
Energy in the SHO This graph shows the potential energy function of a spring. The total energy is constant.

Energy in the Simple Harmonic Oscillator The total energy is, therefore And we can write: (11 -4 c) This can be solved for the velocity as a function of position: where

Energy in the SHO Energy calculations. For the simple harmonic oscillation where k = 19. 6 N/m, A = 0. 100 m, x = -(0. 100 m) cos 8. 08 t, and v = (0. 808 m/s) sin 8. 08 t, determine (a) the total energy, (b) the kinetic and potential energies as a function of time, (c) the velocity when the mass is 0. 050 m from equilibrium, (d) the kinetic and potential energies at half amplitude (x = ± A/2).

Solution:

Solution:

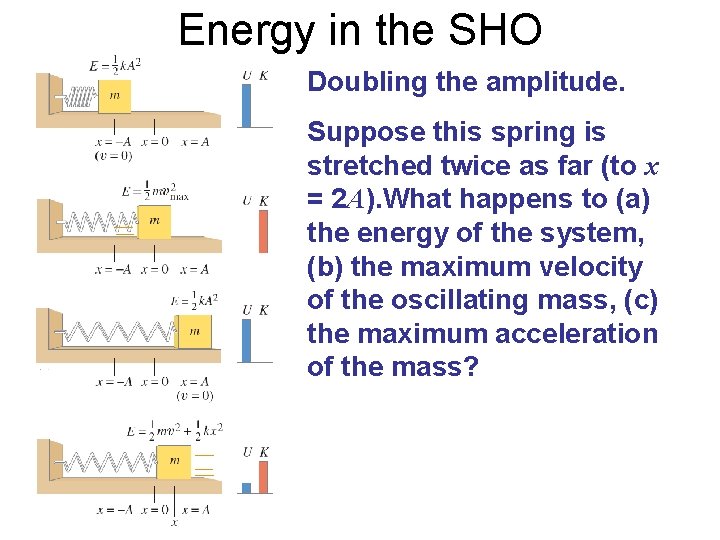
Energy in the SHO Doubling the amplitude. Suppose this spring is stretched twice as far (to x = 2 A). What happens to (a) the energy of the system, (b) the maximum velocity of the oscillating mass, (c) the maximum acceleration of the mass?

Solution:

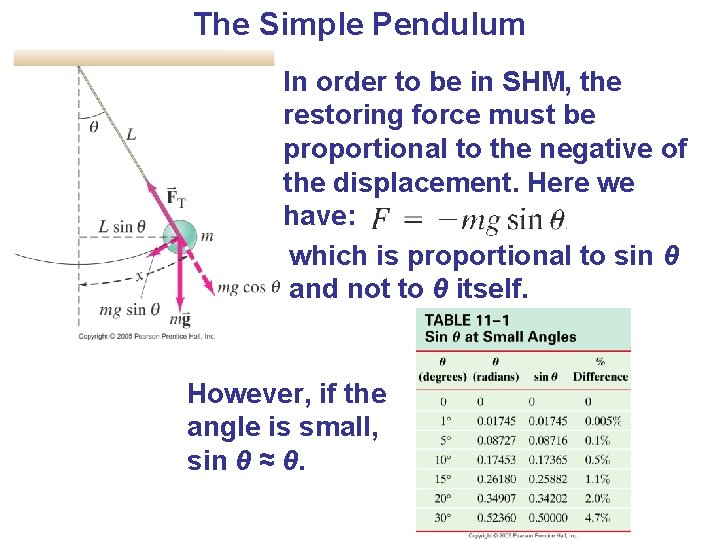
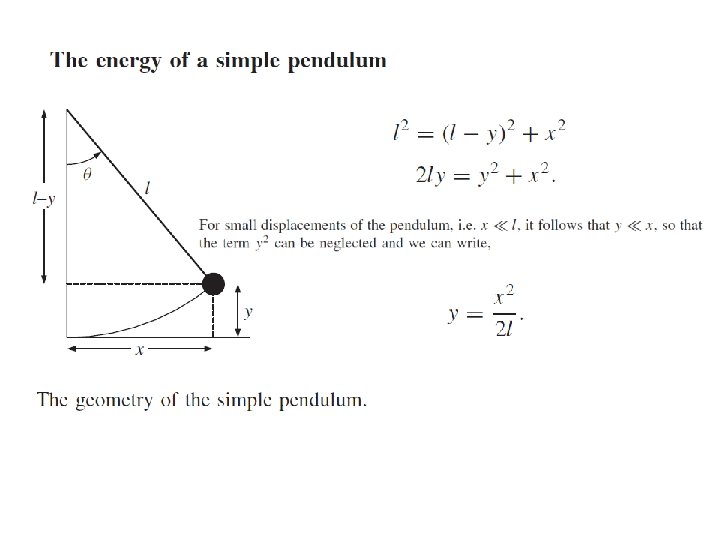
The Simple Pendulum In order to be in SHM, the restoring force must be proportional to the negative of the displacement. Here we have: which is proportional to sin θ and not to θ itself. However, if the angle is small, sin θ ≈ θ.

The Simple Pendulum Therefore, for small angles, we have: where The period and frequency are:

Oscillations in an LC Circuit

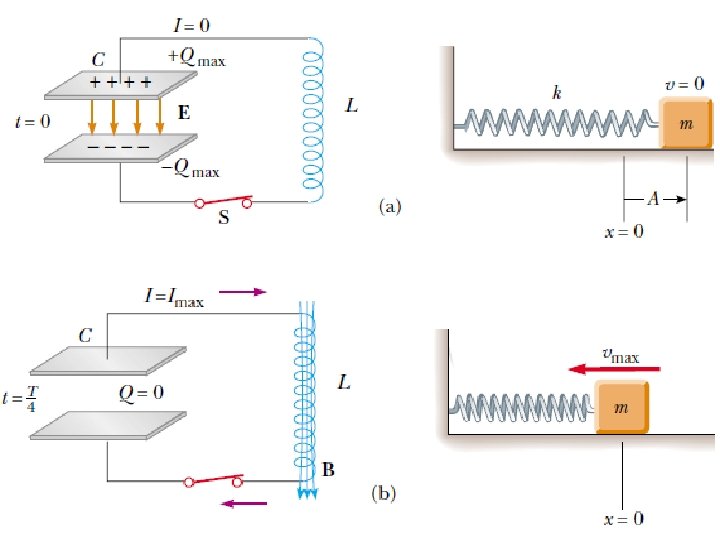
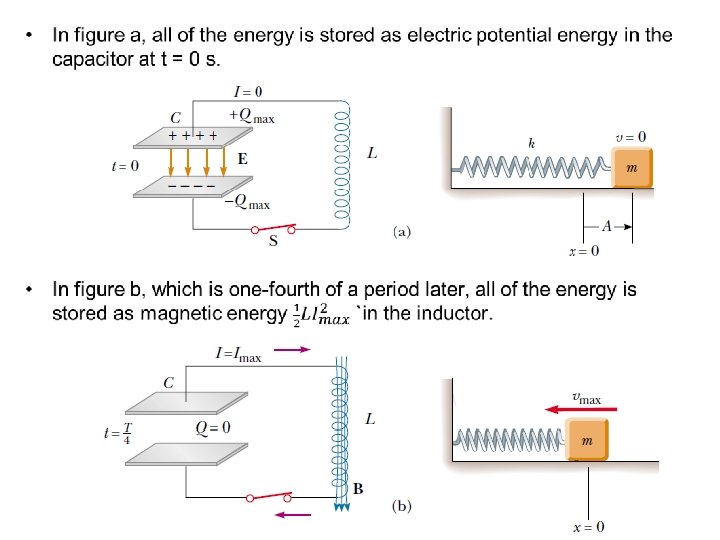
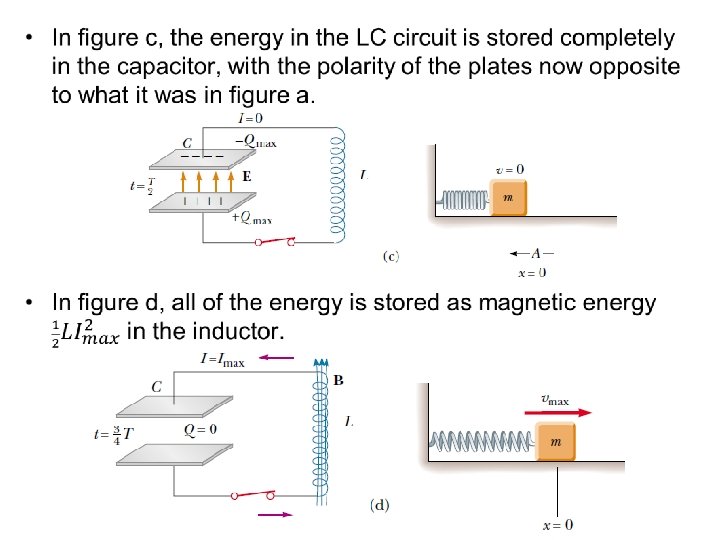
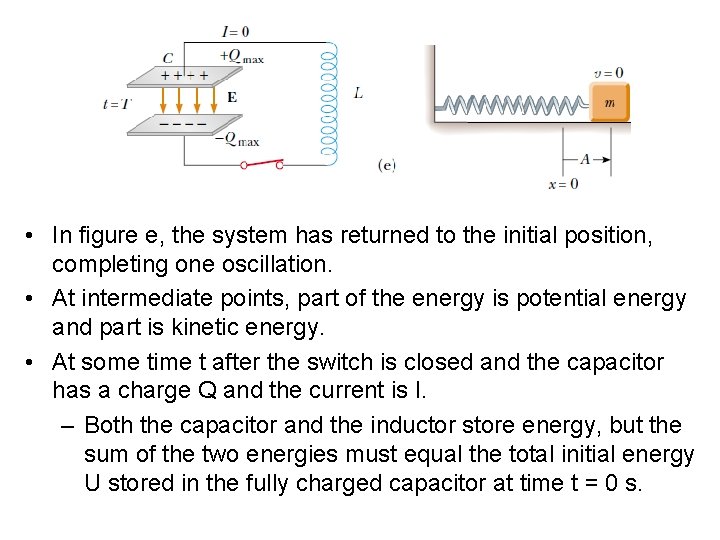
• In figure e, the system has returned to the initial position, completing one oscillation. • At intermediate points, part of the energy is potential energy and part is kinetic energy. • At some time t after the switch is closed and the capacitor has a charge Q and the current is I. – Both the capacitor and the inductor store energy, but the sum of the two energies must equal the total initial energy U stored in the fully charged capacitor at time t = 0 s.

– Since the circuit resistance is zero, no energy is dissipated as joule heat and the total energy must remain constant over time. – Therefore: • Differentiating the energy equation with respect to time and noting that Q and I vary with time:

• We can reduce the equation to a differential equation of one variable by using the following relationships:

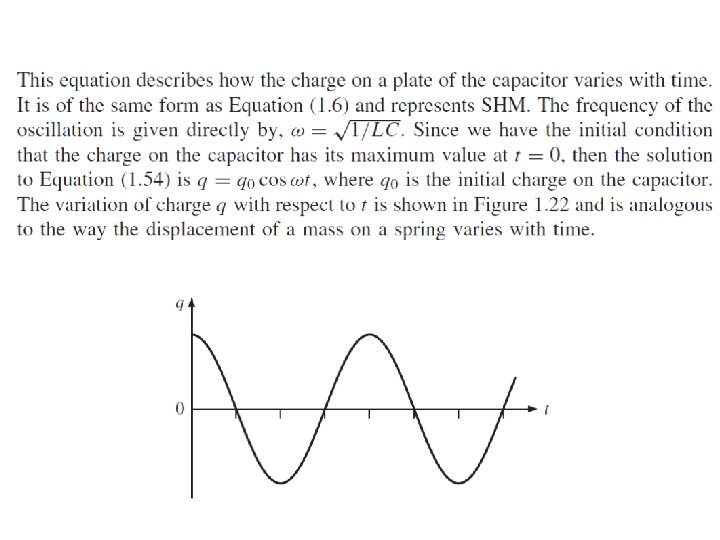
• We can solve for the function Q by noting that the equation is of the same form as that of the mass-spring system (simple harmonic oscillator): – where k is the spring constant, m is the mass, and – The solution for the equation has the general form – where ω is the angular frequency of the simple harmonic motion, A is the amplitude of the motion (the maximum value of x), and is the phase constant; the values of A and depend on the initial conditions.

• Writing in the same form as the differential equation of the simple harmonic oscillator, the solution is: – where Qm is the maximum charge of the capacitor and the angular frequency ω is given by: – The angular frequency of the oscillation depends on the inductance and capacitance of the circuit. • Since Q varies periodically, the current also varies periodically.

• Differentiating the harmonic oscillator equation for the LC oscillator with respect to time:

• To determine the value of the phase angle , examine the initial conditions. In the situation presented, when t = 0 s, I = 0 A, and Q = Q m.

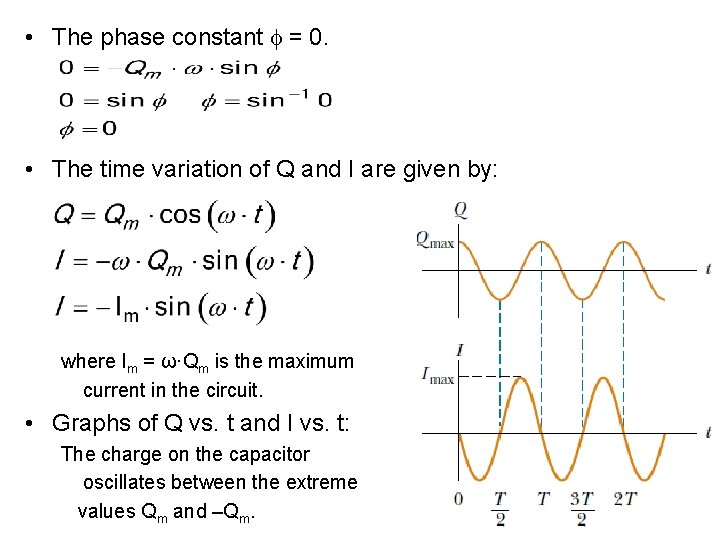
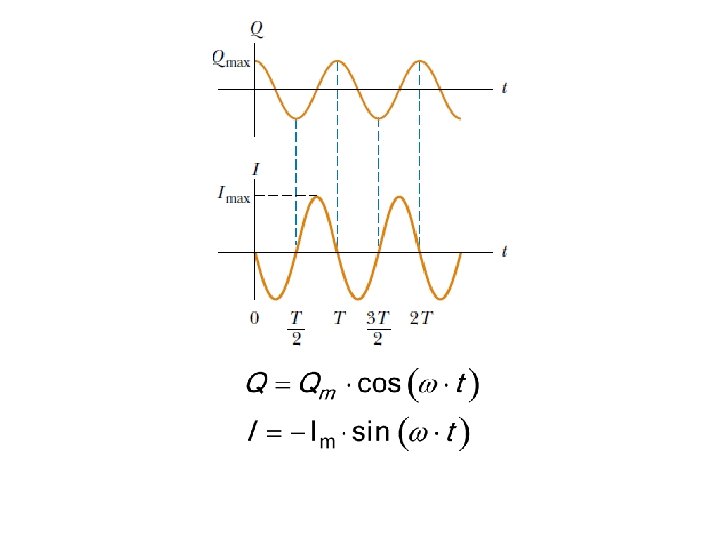
• The phase constant = 0. • The time variation of Q and I are given by: where Im = ω·Qm is the maximum current in the circuit. • Graphs of Q vs. t and I vs. t: The charge on the capacitor oscillates between the extreme values Qm and –Qm.

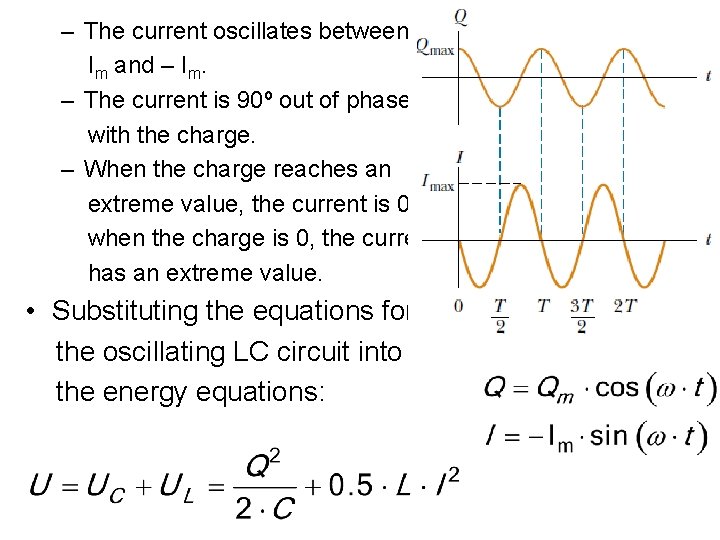
– The current oscillates between Im and – Im. – The current is 90º out of phase with the charge. – When the charge reaches an extreme value, the current is 0; when the charge is 0, the current has an extreme value. • Substituting the equations for the oscillating LC circuit into the energy equations:

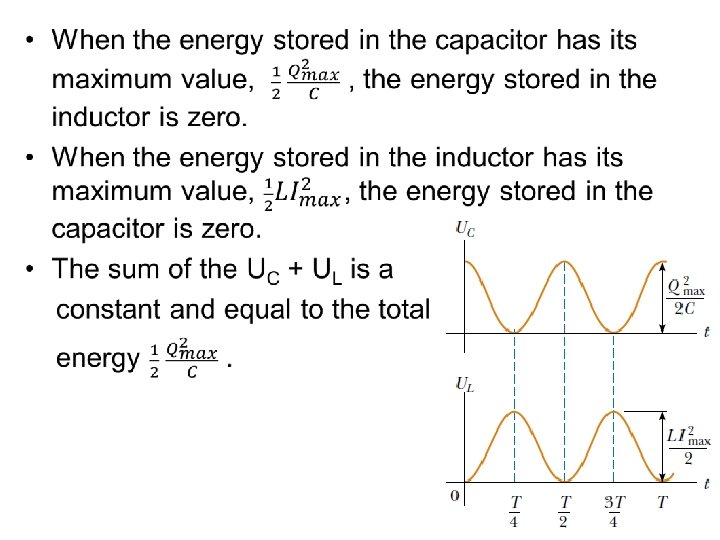
• Total energy: • The equation shows that the energy of the system continuously oscillates between energy stored in the electric field of the capacitor and energy stored in the magnetic field of the inductor.

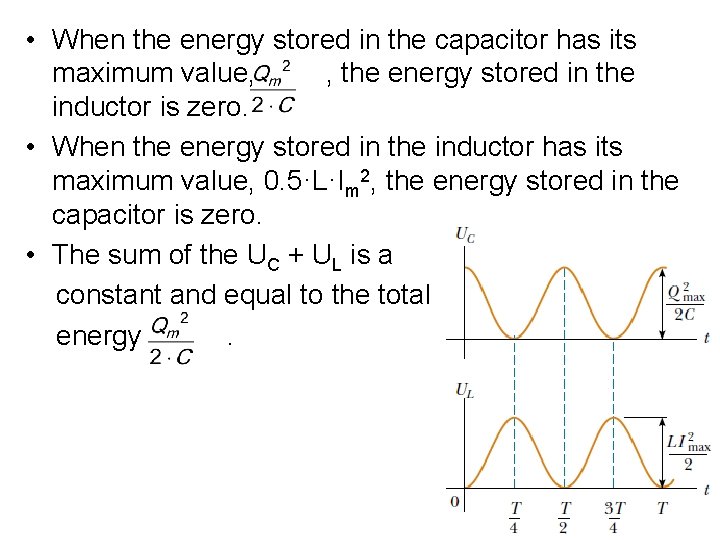
• When the energy stored in the capacitor has its maximum value, , the energy stored in the inductor is zero. • When the energy stored in the inductor has its maximum value, 0. 5·L·Im 2, the energy stored in the capacitor is zero. • The sum of the UC + UL is a constant and equal to the total energy .

• Since the maximum energy stored in the capacitor (when I = 0) must equal the maximum energy stored in the inductor (when Q = 0), • Substituting this into the total energy equation:

• The total energy U remains constant only if the energy losses are neglected. • In actual circuits, there will always be some resistance and so energy will be lost in the form of heat. • Even when the energy losses due to wire resistance are neglected, energy will also be lost in the form of electromagnetic waves radiated by the circuit.

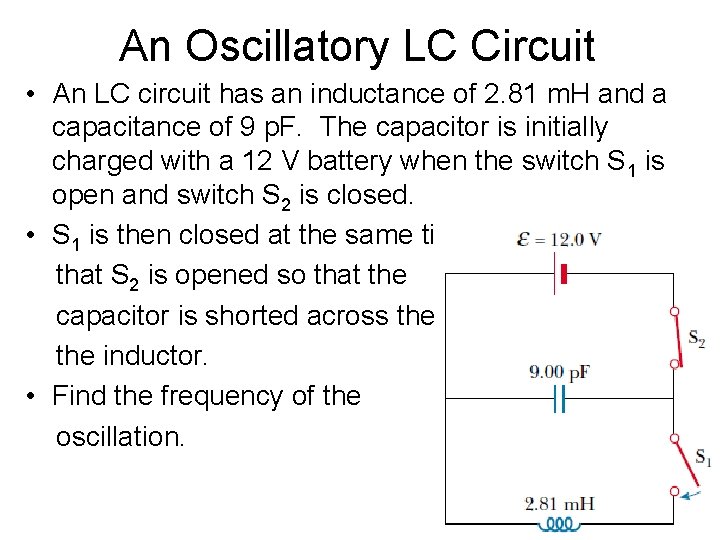
An Oscillatory LC Circuit • An LC circuit has an inductance of 2. 81 m. H and a capacitance of 9 p. F. The capacitor is initially charged with a 12 V battery when the switch S 1 is open and switch S 2 is closed. • S 1 is then closed at the same time that S 2 is opened so that the capacitor is shorted across the inductor. • Find the frequency of the oscillation.

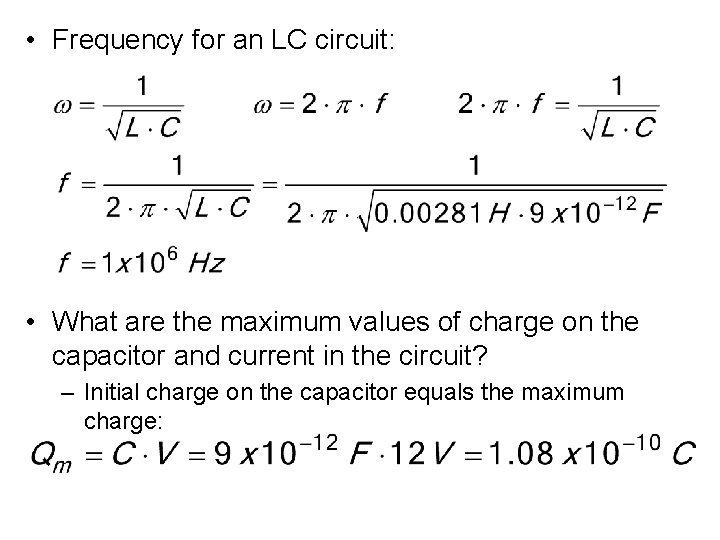
• Frequency for an LC circuit: • What are the maximum values of charge on the capacitor and current in the circuit? – Initial charge on the capacitor equals the maximum charge:

• Maximum current is related to the maximum charge: • Determine the charge and current as functions of time.

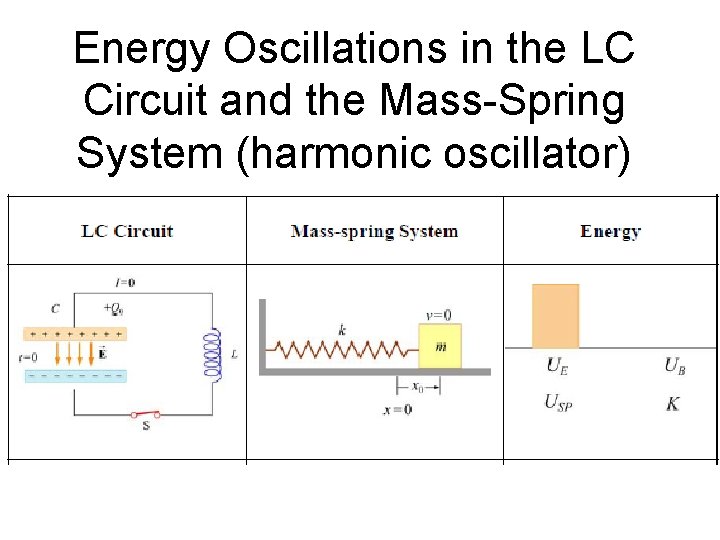
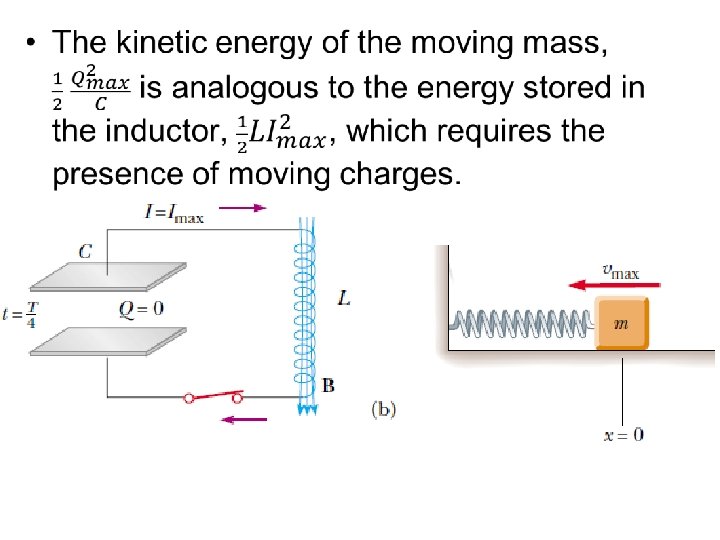
Energy Oscillations in the LC Circuit and the Mass-Spring System (harmonic oscillator)

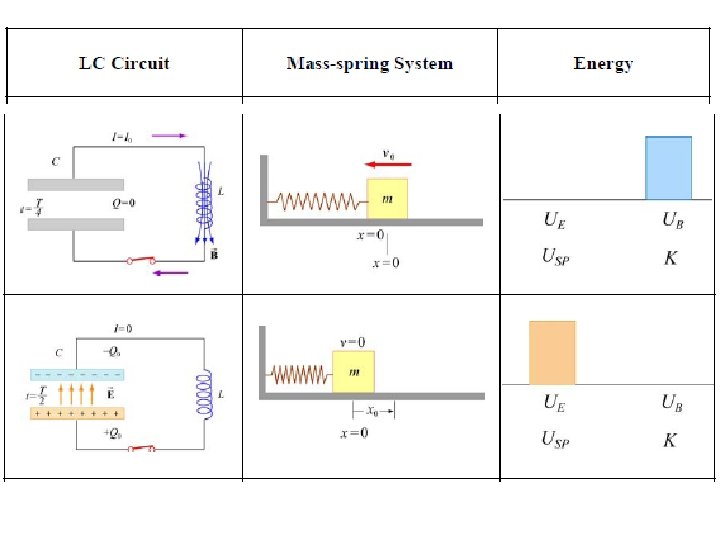
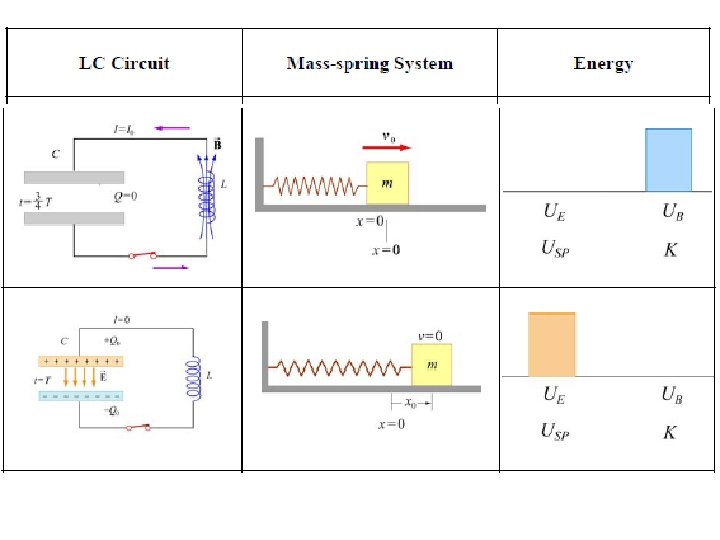
Vibration and Waves The Period and Sinusoidal Nature of SHM

The Period and Sinusoidal Nature of SHM The Period of an object undergoing SHM is independent of the amplitude Imagine an object traveling in a circular pathway If we look at the motion in just the x axis, the motion is analogous to SHM

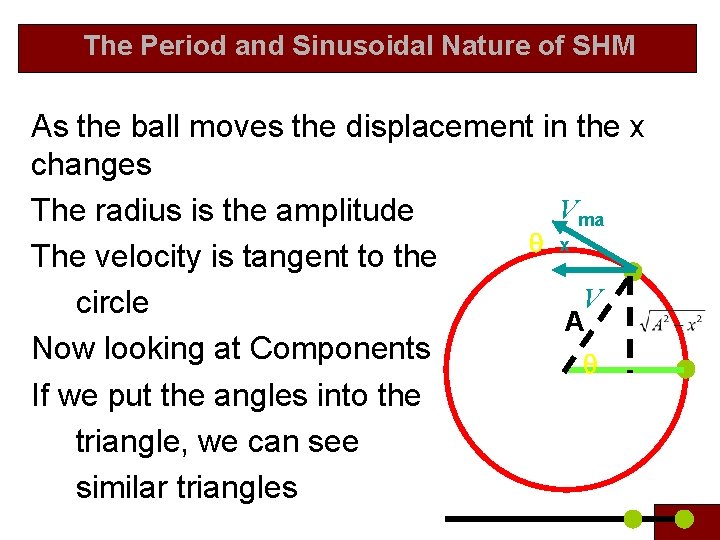
The Period and Sinusoidal Nature of SHM As the ball moves the displacement in the x changes Vma The radius is the amplitude q x The velocity is tangent to the V circle A Now looking at Components q If we put the angles into the triangle, we can see similar triangles

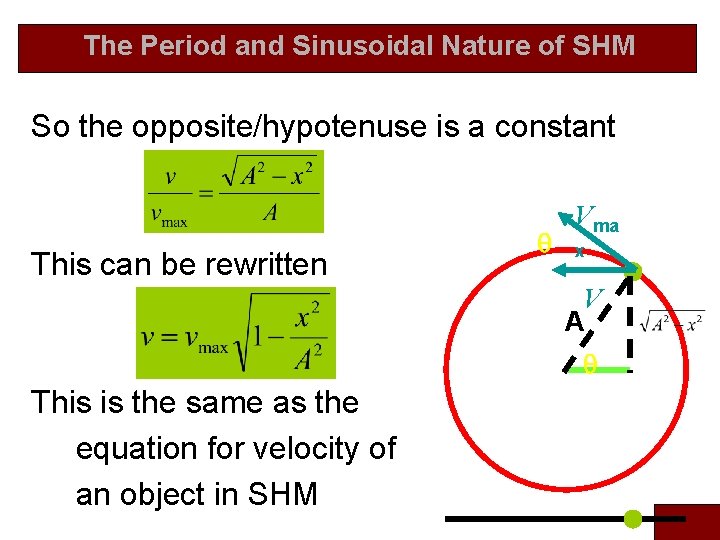
The Period and Sinusoidal Nature of SHM So the opposite/hypotenuse is a constant This can be rewritten q Vma x V A q This is the same as the equation for velocity of an object in SHM

The Period and Sinusoidal Nature of SHM The period would be the time for one complete revolution The radius is the same as the amplitude, and the time for one revolution is the period

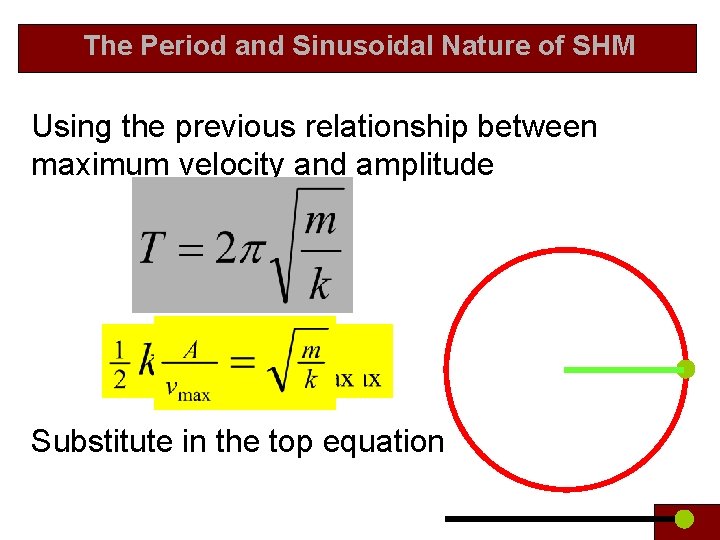
The Period and Sinusoidal Nature of SHM Using the previous relationship between maximum velocity and amplitude Substitute in the top equation

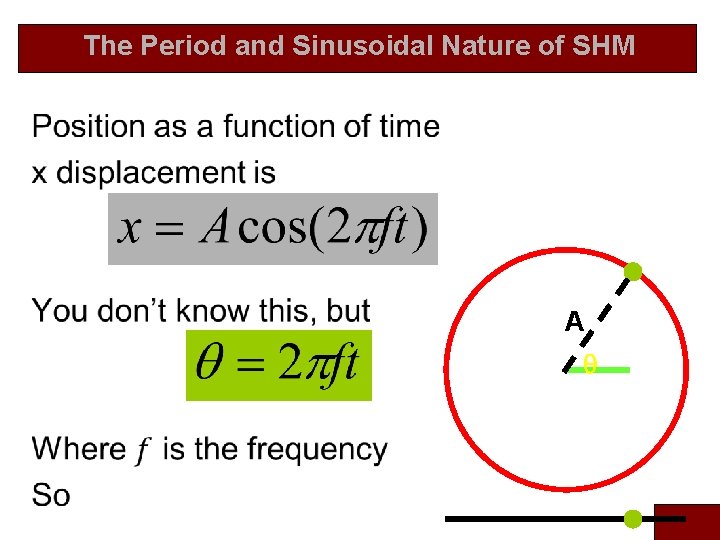
The Period and Sinusoidal Nature of SHM A q

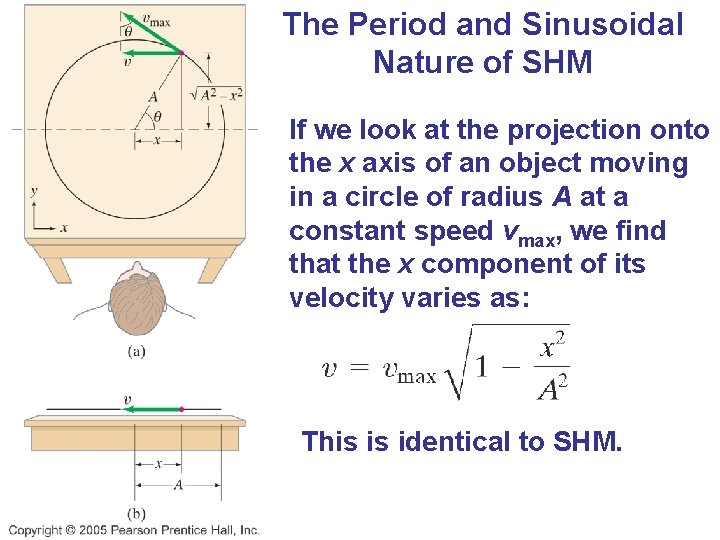
The Period and Sinusoidal Nature of SHM If we look at the projection onto the x axis of an object moving in a circle of radius A at a constant speed vmax, we find that the x component of its velocity varies as: This is identical to SHM.

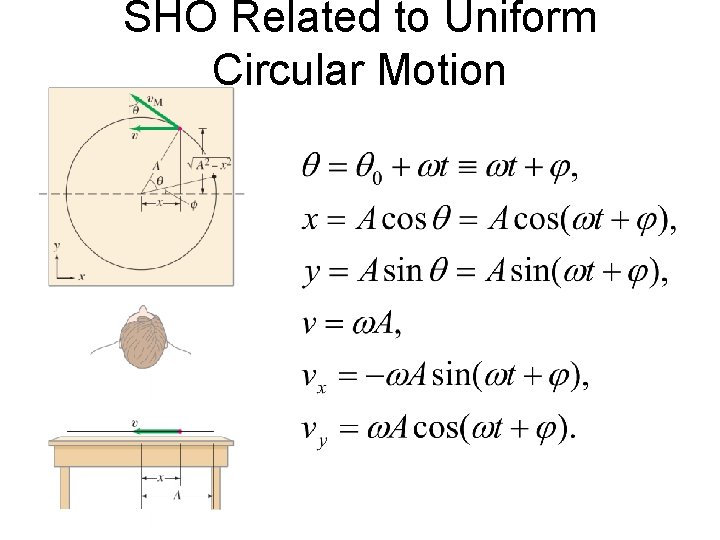
SHO Related to Uniform Circular Motion

The Period and Sinusoidal Nature of SHM Therefore, we can use the period and frequency of a particle moving in a circle to find the period and frequency:

The Period and Sinusoidal Nature of SHM We can similarly find the position as a function of time:

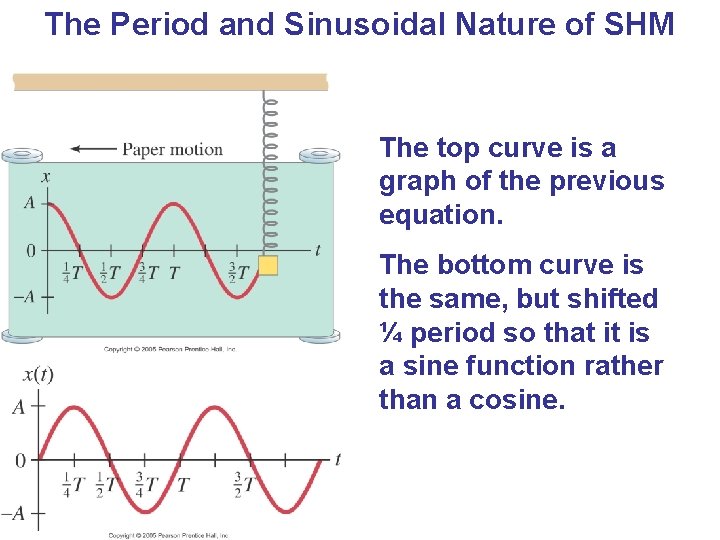
The Period and Sinusoidal Nature of SHM The top curve is a graph of the previous equation. The bottom curve is the same, but shifted ¼ period so that it is a sine function rather than a cosine.

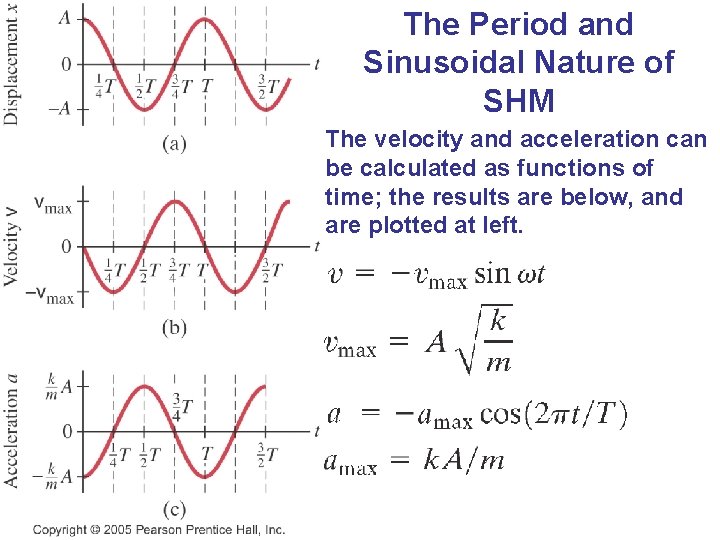
The Period and Sinusoidal Nature of SHM The velocity and acceleration can be calculated as functions of time; the results are below, and are plotted at left.