Vibration Control Presentation in Control engineering research seminar

Vibration Control Presentation in Control engineering research seminar 21. 2. 2011
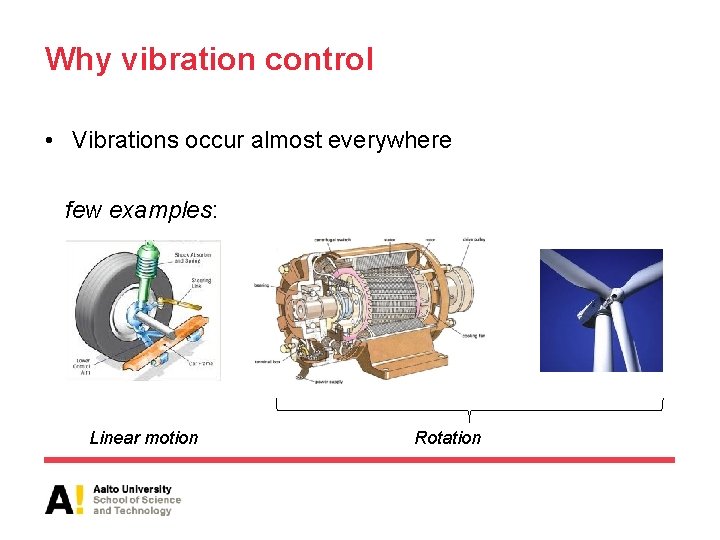
Why vibration control • Vibrations occur almost everywhere few examples: Linear motion Rotation

Why vibrations control • Vibrations are damped to get – Less noise to surroundings -> comfort for users – Decrease conduction of vibration into the structures -> comfort for users/operators – Less wear of parts and need for maintenance -> less costs

Passive and active vibration control Vibrations can be controlled Materials and structures are chosen/designed such that the vibrations are minimized Passively + cheap to design and maintain - works well only on small frequency band An actuator is added to the system to exert opposite force to damp vibrations + more effective on all frequencies and for all kinds of disturbances - expensive to design and maintain

Active vibration control • Vibration control consists of (as almost every control problem) System modeling - How the system is modeled? How accurate model should be chosen? Measurement and estimation - What can be measured directly? What needs to be estimated? Depends on the model structure - What can be controlled? Depends on the model structure and the measurements Control
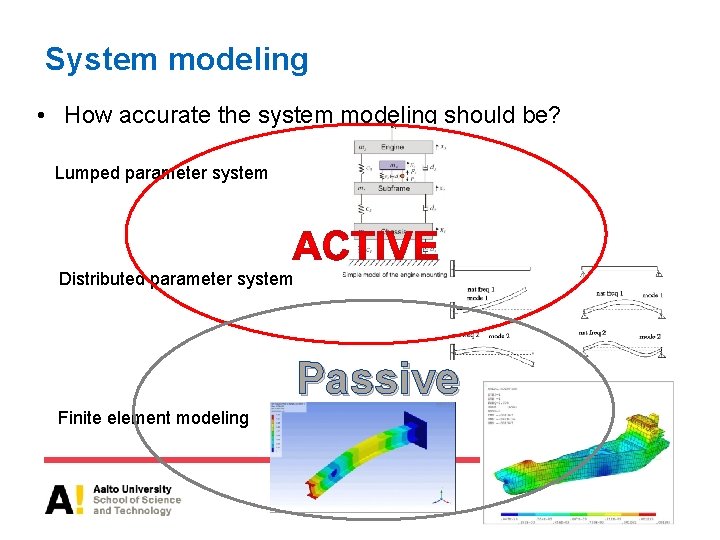
System modeling • How accurate the system modeling should be? Lumped parameter system Distributed parameter system Passive Finite element modeling
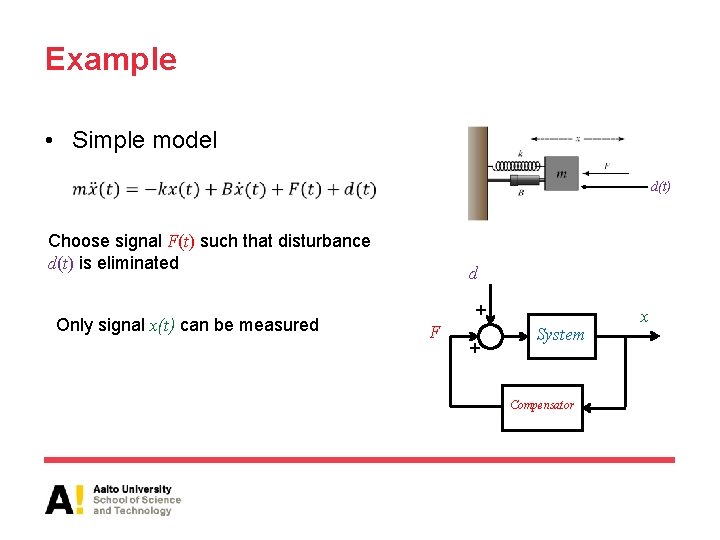
Example • Simple model d(t) Choose signal F(t) such that disturbance d(t) is eliminated Only signal x(t) can be measured d + F + System Compensator x

Vibrations in electrical machines • Structure of an AC induction motor
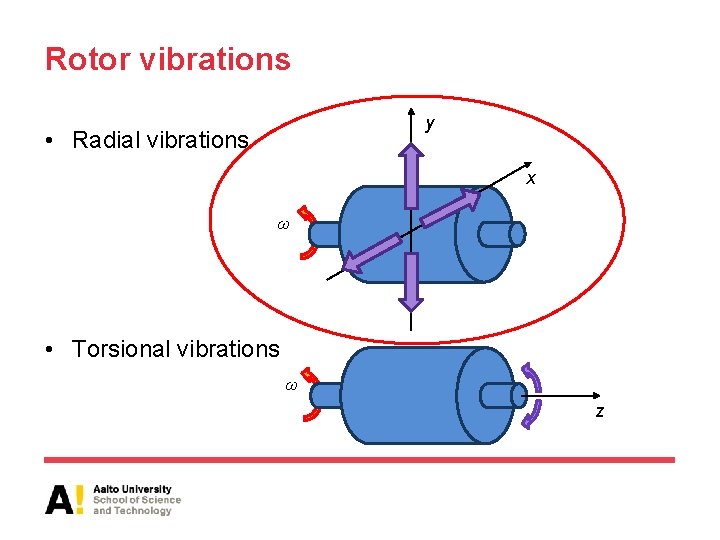
Rotor vibrations y • Radial vibrations x ω • Torsional vibrations ω z
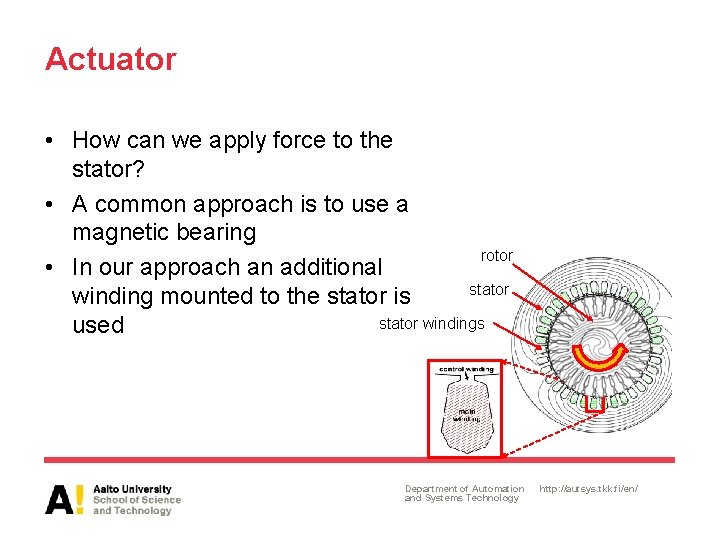
Actuator • How can we apply force to the stator? • A common approach is to use a magnetic bearing rotor • In our approach an additional stator winding mounted to the stator is stator windings used Department of Automation and Systems Technology http: //autsys. tkk. fi/en/
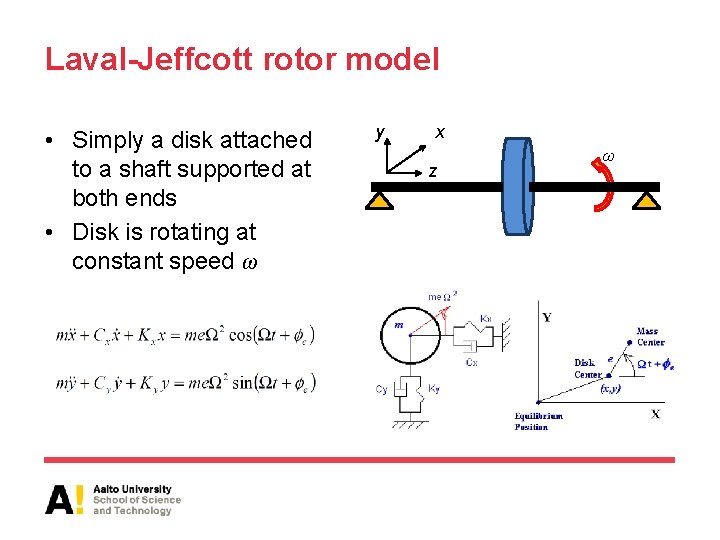
Laval-Jeffcott rotor model • Simply a disk attached to a shaft supported at both ends • Disk is rotating at constant speed ω y x z ω
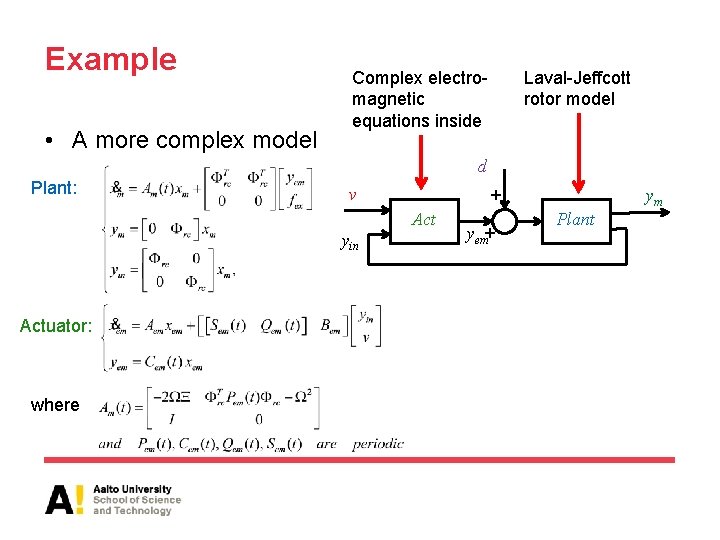
Example • A more complex model Complex electromagnetic equations inside Laval-Jeffcott rotor model d Plant: v Act yin Actuator: where ym + yem+ Plant
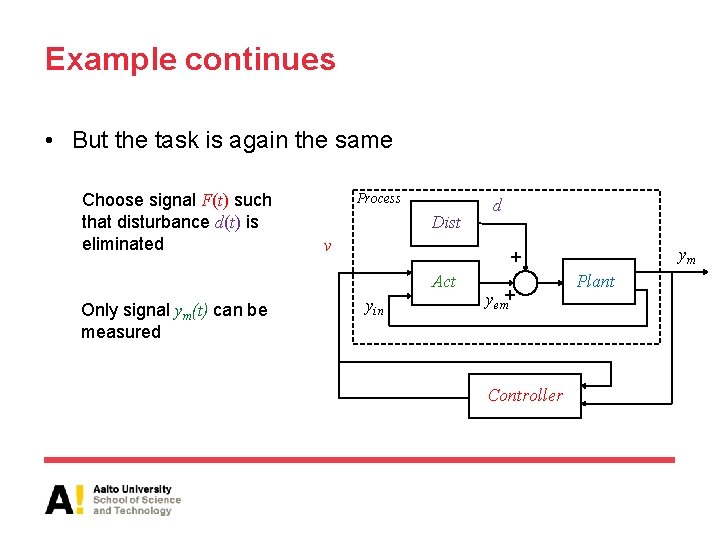
Example continues • But the task is again the same Choose signal F(t) such that disturbance d(t) is eliminated Process Dist v ym + Act Only signal ym(t) can be measured d yin yem+ Controller Plant
- Slides: 13