VI 3 Spectrum of compact operators Spectrum of
















































- Slides: 51

VI. 3 Spectrum of compact operators

Spectrum of T Let is called the resolvent set of T : spectrum of T

Eigenvalue and Eigenspace : eigenvalue of T the eigenspace associated If then

Remark 5 In general the inclusion is strict (except when there may exists ): such that and ( such belongs to an eigenvalue) but is not

Example Let then but

Proposition VI. 7 is compact and



Lemma 1. 2 Suppose that is a sequence consisting of totally different numbers such that then i. e. isolated elements. consists only




Theorem VI. 8 Let T is compact and Then (a) (b) (c) is finite or is a sequence tending 0.





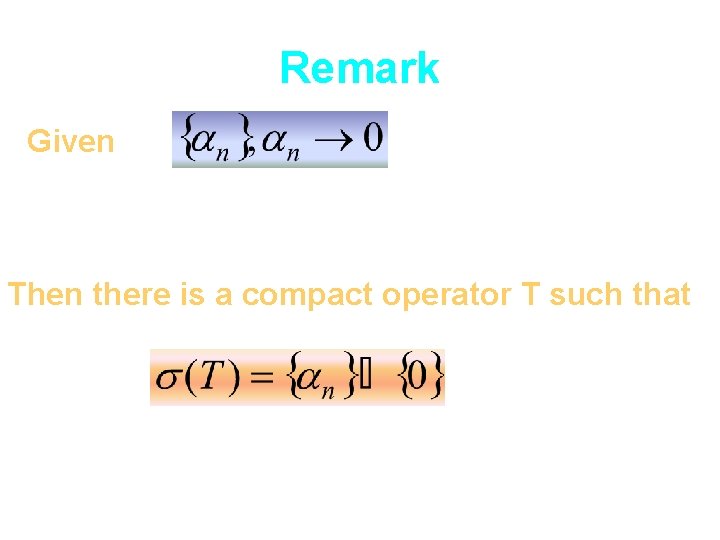
Remark Given Then there is a compact operator T such that



VI. 4 Spectral decomposition of self-adjoint operators

Sesquilinear p. 1 Let X be a complex Hilbert space. is called sesquilinear if

Sesquilinear p. 2 B is called bounded if there is r>0 such that B is called positive definite if there is ρ>0 s. t.

Theorem 5. 1 The Lax-Milgram Theorem p. 1 Let X be a complex Hilbert space and B a a bounded, positive definite sesquilinear functional on X x X , then there is a unique bounded linear operator S: X →X such that and

Theorem 5. 1 The Lax-Milgram Theorem Furthermore exists and is bounded with p. 2

Self-Adjoint E=H is a Hilbert space Definition : if i. e. is called self-adjoint

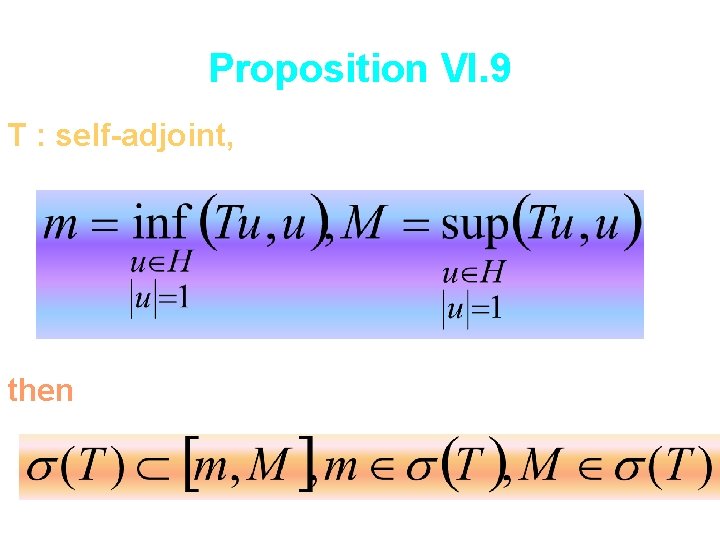
Proposition VI. 9 T : self-adjoint, then

Remark of Proposition This Proposition is better than Thm VI. 7




Corollary VI. 10 Let then T=0 and


Propositions p. 1 Let be an orthogonal system in a Hilbert space X, and let U be the closed vector subspace generated by Let and be the orthogonal projection onto U where

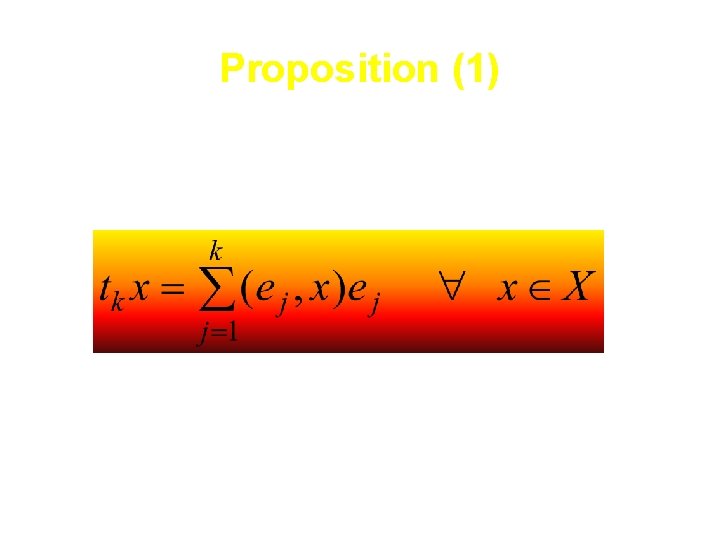
Proposition (1)

Proposition (2)

Proposition (3) For each k and x, y in X

Proposition (4) For any x, y in X

Proposition (5) Bessel inequality

Proposition (6) ( Parseval relation) An orthonormal system is called complete and a Hilbert basis if U=X

Separable A Hilbert space is called separable if it contains a countable dense subset

Theorem VI. 11 H: a separable Hilbert space T: self-adjoint compact operator. Then it admits a Hilbert basis formed by eigenvectors of T.







VI. 1 Definition. Elementary Properties Adjoint

Lemma VI. 1 (Riesz-Lemma) Let For any fixed , apply Green’s second identity to u and then let in the domain we have

 Web buckling and web crippling slideshare
Web buckling and web crippling slideshare Line spectrum and continuous spectrum difference
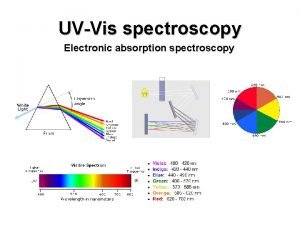
Line spectrum and continuous spectrum difference Absorption spectrum
Absorption spectrum Hexagonal compact
Hexagonal compact Formulation of face powder
Formulation of face powder Rowenta compact power cyclonic ro3731
Rowenta compact power cyclonic ro3731 Standard form scientific notation
Standard form scientific notation Mayflower compact purpose
Mayflower compact purpose Compact state definition
Compact state definition Compact space chamber with cross valve technology
Compact space chamber with cross valve technology Compact plano helical
Compact plano helical Suspension definition pharmacy
Suspension definition pharmacy Aggregating local image descriptors into compact codes
Aggregating local image descriptors into compact codes Cms compact muon solenoid
Cms compact muon solenoid Mayflower compact purpose
Mayflower compact purpose Mayflower compact summary
Mayflower compact summary Compact states examples
Compact states examples Compact city
Compact city Costal cartilage
Costal cartilage Nation state ap human geography
Nation state ap human geography Longitudinal section of a long bone
Longitudinal section of a long bone Mayflower compact
Mayflower compact Oxo connect
Oxo connect Pari junior boy
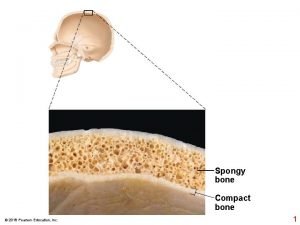
Pari junior boy Compact bone
Compact bone Compact heater 4000
Compact heater 4000 Compact city
Compact city Indiana campus compact
Indiana campus compact Compact multi-signatures for smaller blockchains
Compact multi-signatures for smaller blockchains In the name of god amen
In the name of god amen Mayflower101
Mayflower101 7 steps of the scientific method
7 steps of the scientific method Meaning of massachusetts
Meaning of massachusetts Pid 3 step
Pid 3 step Historiograma
Historiograma New york campus compact
New york campus compact Massive compact halo objects
Massive compact halo objects Multiplicité maille hexagonale compacte
Multiplicité maille hexagonale compacte Sql compact
Sql compact Planmeca compact classic
Planmeca compact classic Compact clay soil
Compact clay soil Tesut animal epitelial
Tesut animal epitelial Bone cell
Bone cell Territoriality
Territoriality Un global compact
Un global compact Ezekiel maize
Ezekiel maize Ohio deans compact
Ohio deans compact Mayflower compact main idea
Mayflower compact main idea Compact and spongy bone
Compact and spongy bone Compact fluorescent lamp
Compact fluorescent lamp Compressed trie example
Compressed trie example Opacifier in cosmetics examples
Opacifier in cosmetics examples