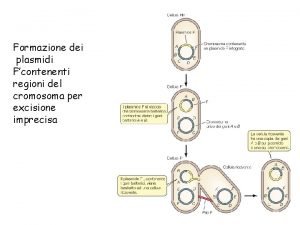
Vettori Definizione e sue rappresentazioni Definizione di vettore

Vettori Definizione e sue rappresentazioni

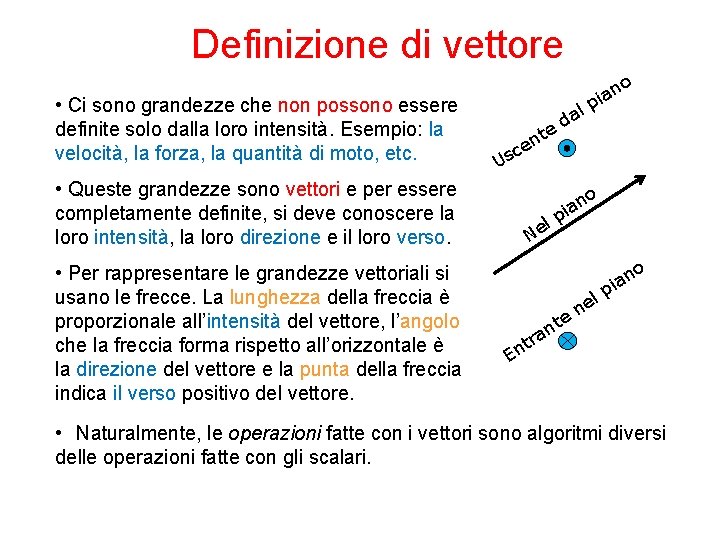
Definizione di vettore • Ci sono grandezze che non possono essere definite solo dalla loro intensità. Esempio: la velocità, la forza, la quantità di moto, etc. • Queste grandezze sono vettori e per essere completamente definite, si deve conoscere la loro intensità, la loro direzione e il loro verso. • Per rappresentare le grandezze vettoriali si usano le frecce. La lunghezza della freccia è proporzionale all’intensità del vettore, l’angolo che la freccia forma rispetto all’orizzontale è la direzione del vettore e la punta della freccia indica il verso positivo del vettore. o te n e l n pia da c Us l Ne p e tr n E t an o ian lp e n o n ia • Naturalmente, le operazioni fatte con i vettori sono algoritmi diversi delle operazioni fatte con gli scalari.

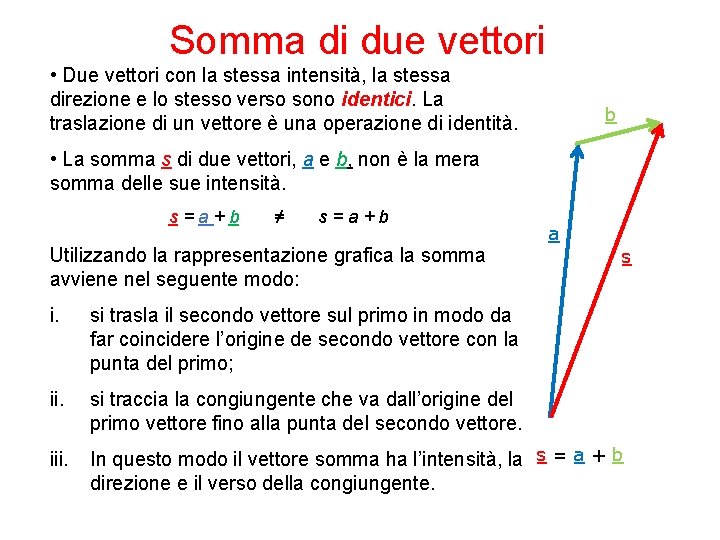
Somma di due vettori • Due vettori con la stessa intensità, la stessa direzione e lo stesso verso sono identici. La traslazione di un vettore è una operazione di identità. b • La somma s di due vettori, a e b, non è la mera somma delle sue intensità. s=a+b ≠ s=a+b Utilizzando la rappresentazione grafica la somma avviene nel seguente modo: a s i. si trasla il secondo vettore sul primo in modo da far coincidere l’origine de secondo vettore con la punta del primo; ii. si traccia la congiungente che va dall’origine del primo vettore fino alla punta del secondo vettore. iii. In questo modo il vettore somma ha l’intensità, la s = a + b direzione e il verso della congiungente.

Somma di più vettori • Due vettori sono opposti se hanno la stessa intensità, la stessa direzione, ma verso opposto. • Per fare la differenza di due vettori basta sommare al primo vettore l’opposto del secondo vettore. • Il vettore f = m – n è equivalente a f = m + (-n) • La somma di più vettori: s=a+b–c+d b c a a -c b d s d

Vettori perpendicolari Nel caso particolare della somma di due vettori perpendicolari possiamo dire che il vettore risultante è l’ipotenusa di un triangolo rettangolo i cui cateti sono i vettori da sommare. i h b Ovviamente la risultante del vettore somma ha un modulo che è dato dal teorema di Pitagora i 2 = b 2 + h 2

Segmento nello spazio • Il concetto di vettore, è molto utile per conoscere la natura delle grandezze fisiche e anche molto utile nella descrizione della geometria Euclidea. • In un triangolo rettangolo, se sono note le lunghezze dei due cateti, saranno noti: la lunghezza dell’ipotenusa e gli angolo che l’ipotenusa forma con i cateti a 2 = b 2 + c 2 g = arctg c/b = tan -1 c/b a g b c b g = 90°- b La lunghezza e la direzione di qualsiasi segmento si può trovare conoscendo la lunghezza delle sue proiezioni su gli assi cartesiani.

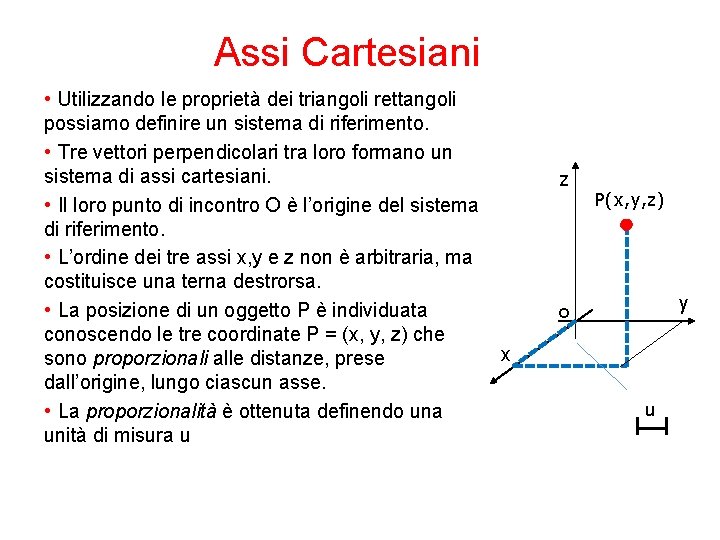
Assi Cartesiani • Utilizzando le proprietà dei triangoli rettangoli possiamo definire un sistema di riferimento. • Tre vettori perpendicolari tra loro formano un sistema di assi cartesiani. • Il loro punto di incontro O è l’origine del sistema di riferimento. • L’ordine dei tre assi x, y e z non è arbitraria, ma costituisce una terna destrorsa. • La posizione di un oggetto P è individuata conoscendo le tre coordinate P = (x, y, z) che sono proporzionali alle distanze, prese dall’origine, lungo ciascun asse. • La proporzionalità è ottenuta definendo una unità di misura u z P(x, y, z) y o x u

Coordinate Polari • La posizione di un punto può essere individuata anche usando sistemi di coordinate diversi: per esempio le coordinate polari. • Un punto sarà individuato conoscendo la lunghezza del segmento r che va dall’origine al punto P, e da gli angoli q e f definiti come in figura. • Di conseguenza le relazioni di trasformazione fra le coordinate cartesiane e le coordinate sferiche sono: z P q r y O x f H

Relazioni invertite • Se conoscendo le coordinate cartesiane è possibile ricavare le coordinate polari, dalle coordinate polari è possibile risalire alle coordinate cartesiane. z P q r O f x y H • La coordinata x non è altro che la proiezione del segmento OH sull’asse x ovvero OH cosf. • Ma OH è a sua volta r sinq quindi x = r sinq cosf • Analogamente la coordinata y sarà la proiezione di OH sull’asse y ovvero OH sinf , ma OH vale r sinq quindi y = r sinq sinf • Infine la coordinata z è la proiezione di OP sull’asse Z, ovvero OP cosq e quindi z = r cosq

Le regole dell’algebra vettoriale • Sapendo che ogni vettore è la somma di tre vettori perpendicolari, potremo definire tre vettori di lunghezza unitaria i, j, k (versori) e formare un sistema di riferimento cartesiano. • Il vettore r che unisce l’origine del nostro sistema di riferimento O ad un punto generico dello spazio P(xp, yp, zp) sarà descritto da: r = x pi + y pj + z pk dove i coefficienti dei versori sono le coordinate del vettore r la cui origine è in O e il vertice in P • I coefficienti di r sono i suoi coseni direttori z x = r cosa z y = r cosb k j y g r z = r cosg a b y x x i