VETORES GRANDEZAS FSICAS Podemos dizer de modo mais

VETORES

GRANDEZAS FÍSICAS Podemos dizer de modo mais usual que grandeza é tudo aquilo que pode variar quantitativamente. Deste modo, grandezas físicas são as que podem ser medidas. São divididas em dois grupos: escalares e vetoriais.

GRANDEZAS ESCALARES E VETORIAIS Grandezas escalares: ficam totalmente expressas por um valor e uma unidade. Exemplos: temperatura, massa, calor, tempo, etc. Grandezas vetoriais: são aquelas que não ficam totalmente determinadas com um valor e uma unidade, para que fiquem totalmente definidas necessitam de módulo (número com unidade de medida), direção e sentido. Exemplos: velocidade, força, aceleração, etc.

VETORES Ente matemático abstrato, definido por um valor real (módulo ou intensidade) associado a uma direção e um sentido.

REPRESENTAÇÃO GRÁFICA DE UM VETOR § Para representar graficamente um vetor usamos um segmento de reta orientado. § O módulo do vetor, representa numericamente o comprimento de sua seta. § O vetor acima tem módulo igual a 3 u, que é igual a distância entre os pontos A e B. § Para indicar vetores usamos as seguintes notações: V AB onde: A é a origem e B é a extremidade

PRINCIPAIS CARACTERÍSTICAS DE UM VETOR n Módulo: comprimento do segmento (através de uma escala pré-estabelecida). O módulo de um vetor é indicado utilizando-se duas barras verticais. |A| (Lê-se: módulo de A) n Direção: reta que contém o segmento n Sentido: orientação do segmento

VETOR OPOSTO O vetor oposto é aquele que possui o mesmo módulo, a mesma direção e o sentido oposto. Veja a seguir um exemplo com o vetor e o seu respectivo oposto. A -A

ADIÇÃO VETORIAL n n Determinação do vetor soma, ou vetor resultante a partir de dois ou mais vetores. Pode ser efetuada através do método gráfico e do método analítico.

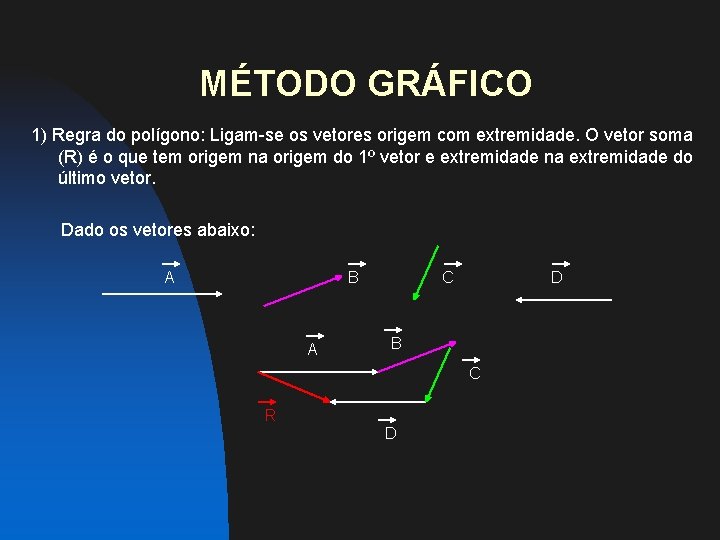
MÉTODO GRÁFICO 1) Regra do polígono: Ligam-se os vetores origem com extremidade. O vetor soma (R) é o que tem origem na origem do 1º vetor e extremidade na extremidade do último vetor. Dado os vetores abaixo: A B A C D B C R D

http: //br. geocities. com/saladefisica 3/laboratorio/vetores. htm http: //br. geocities. com/saladefisica 3/laboratorio/vetores 2. htm

MÉTODO GRÁFICO 2) Regra do Paralelogramo: os dois vetores a serem somados devem estar unidos pela origem. A B A R B

MÉTODO ANALÍTICO Podemos encontrar o módulo da resultante de dois vetores, sabendo-se apenas o módulo dos vetores e o ângulo entre eles. Exemplos: Sejam dois vetores de módulos A e B, e que formam entre si um ângulo θ. 1) Se θ = 0º, os vetores são paralelos, têm a mesma direção e mesmo sentido, conforme figura abaixo: A B O módulo do vetor resultante entre estes dois vetores será a soma dos módulo dos dois, chamado de resultante máxima.

2) Se θ = 180º, os vetores são paralelos, têm a mesma direção e sentidos opostos, conforme figura abaixo: A B O módulo do vetor resultante entre estes dois vetores será a diferença dos módulo dos dois, chamado de resultante mínima. 3) Se θ = 90º, os vetores são perpendiculares, conforme figura abaixo: A B O módulo do vetor resultante entre estes dois vetores será a raiz quadrada da soma dos quadrados módulo dos dois (teorema de Pitágoras).

4) Se θ, for um ângulo qualquer, diferente dos mencionados anteriormente, os vetores são oblíquos, conforme figura abaixo: θ A B O módulo do vetor resultante entre estes dois vetores será dada pela lei dos cosenos:

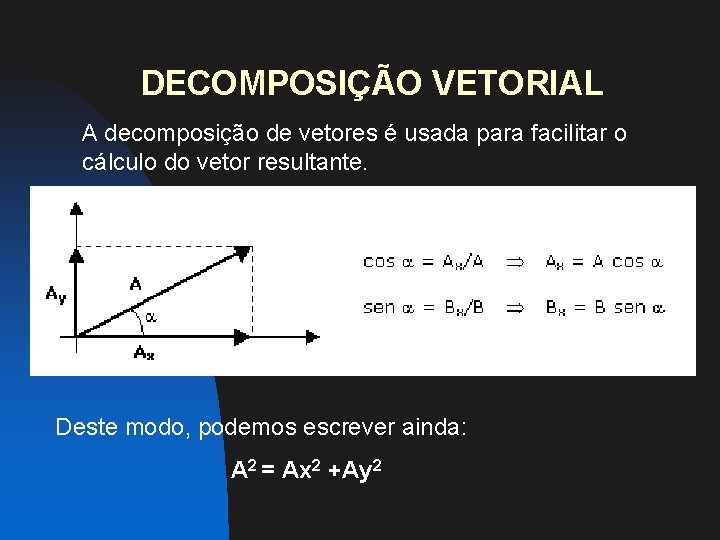
DECOMPOSIÇÃO VETORIAL A decomposição de vetores é usada para facilitar o cálculo do vetor resultante. Deste modo, podemos escrever ainda: A 2 = Ax 2 +Ay 2

MULTIPLICAÇÃO DE UM VETOR POR UM NÚMERO REAL Ao multiplicarmos um vetor qualquer (A) por um número real (n) positivo ou negativo, inteiro ou fracionário, obtemos como resultado um vetor produto (P), com as seguintes condições: § § § O módulo do vetor P é igual a n x |A|. A direção é a mesma de A. O sentido é igual ao de A se n for positivo ou sentido oposto ao de A se n for negativo.

DIVISÃO DE UM VETOR POR UM NÚMERO REAL Ao dividirmos um vetor qualquer (A) por um número real (n) obtemos como resultado um vetor quociente (Q), com as seguintes condições: § § § O módulo do vetor Q é igual a |A|/n. A direção é a mesma de A. O sentido é igual ao de A se n for positivo ou sentido oposto ao de A se n for negativo.