Vertical Line Test Is the Graph a Function

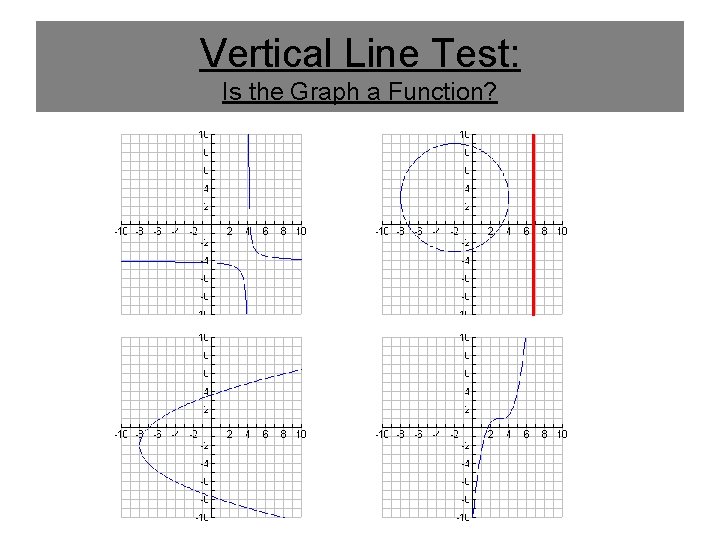
Vertical Line Test: Is the Graph a Function?

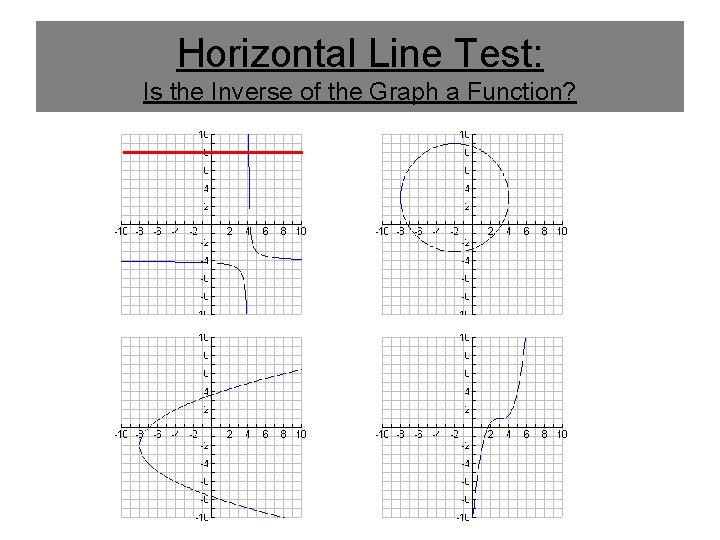
Horizontal Line Test: Is the Inverse of the Graph a Function?

Restricted Domain Find the inverse function of f below: Inverse Function

Restricted Domain Find the inverse function of f below:

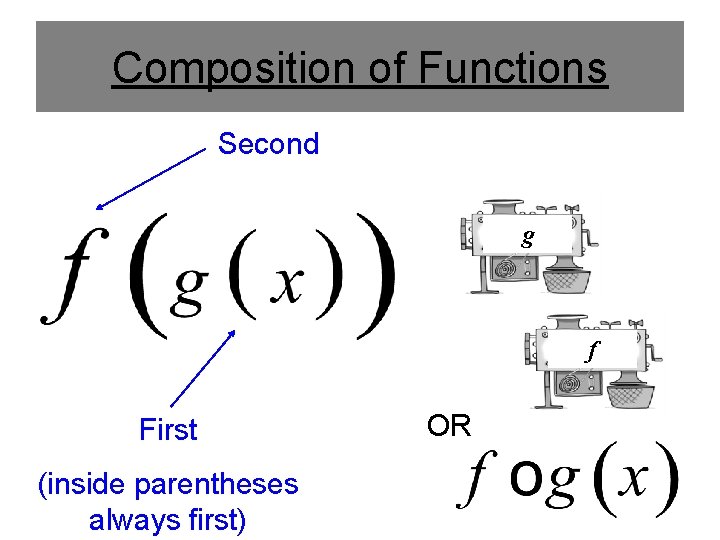
Composition of Functions Second g f First (inside parentheses always first) OR

Inverse and Compositions In order for two functions to be inverses: AND

Algebraically Finding an Inverse Find the inverse functions of the following:

Day 42: November 5 th Objective: Apply strategies for finding inverses to parent graph equations. Begin to think of the inverse function for y=3 x. THEN Define the term logarithm as the inverse exponential function or, when y=bx, “y is the exponent to use with base b to get x. ” • Homework Check • 6 -54 to 6 -58 (pgs 277 -279) • Wells Time • 6 -67 to 6 -71 (pgs 281 -282) • Closure Homework: 6 -59 to 6 -66 (pgs 279 -280) AND 6 -72 to 6 -80 (pgs 283 -284) Project Due: Monday, November 8 th

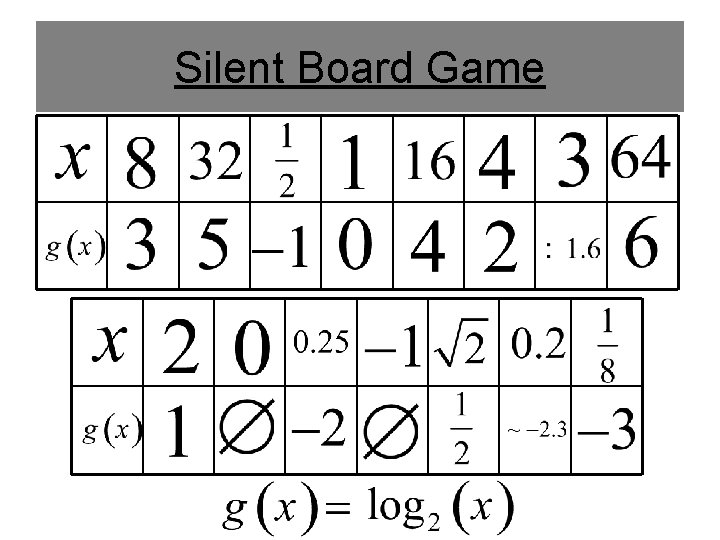
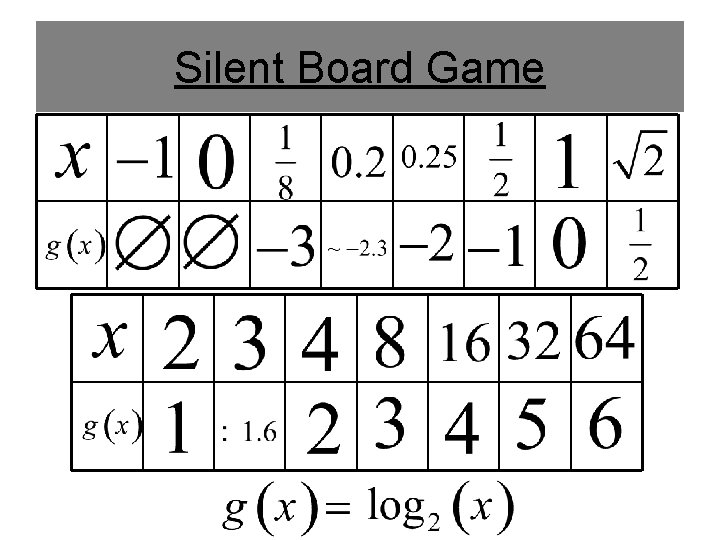
Silent Board Game

Silent Board Game

6 -71: Closure 2 4 7 1. 2 w+3

Logarithm's Undo Exponentials Log’s give you exponents! Inverses Same as

Logarithm and Exponential Forms y = log 2(32) y 2 = 32

Logarithms a>0 b>0 The logarithm base a of b is the exponent you put on a to get b. i. e. Logs give you exponents!

Day 43: November 5 th Objective: Develop methods to graph logarithmic functions with different bases. Rewrite logarithmic equations as exponential equations and find inverses of logarithmic functions. THEN Look into the base of the log key on the calculator. Also extend our knowledge of general equations for parent functions to transform the graph of y=log(x). • Homework Check • 6 -81 and 6 -83 (pgs 285 -286) • Wells Time • 6 -93 and 6 -95 (pgs 288 -289) • Closure Homework: 6 -84 to 6 -92 (pgs 286 -287) AND 6 -96 to 6 -105 (pgs 290 -291)

6 -83: Learning Log Title: The Family of Logarithmic Functions • • • What is the general shape of the graph? What happens to the value of y as x increases? How is the graph related to the exponential graph? What is the Domain? Range? Why is the x-intercept always (1, 0)? Why is the line x=0 (y-axis) always an asymptote? Why is there no horizontal asymptote? How does the graph change if b changes? What does the graph look like when 0<b<1? What does the graph look like when b=1? What does the graph look like when b>1?

Common Logarithm Ten is the common base for logarithms, so log(x) is called a common logarithm and is shorthand for writing log 10(x). You read this as “the logarithm base 10 of x. ” Our calculator has the button log. It doesn’t have the subscript 10 because it stands for the common logarithm: log 10100 = log 100

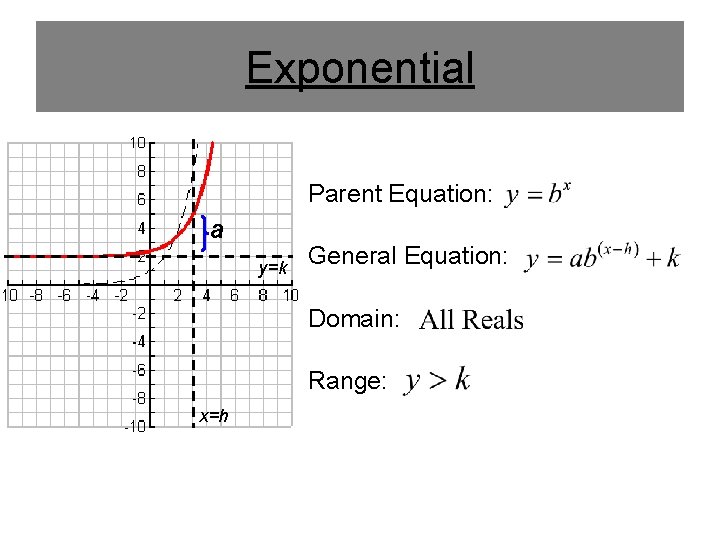
Exponential Parent Equation: a y=k General Equation: Domain: Range: x=h

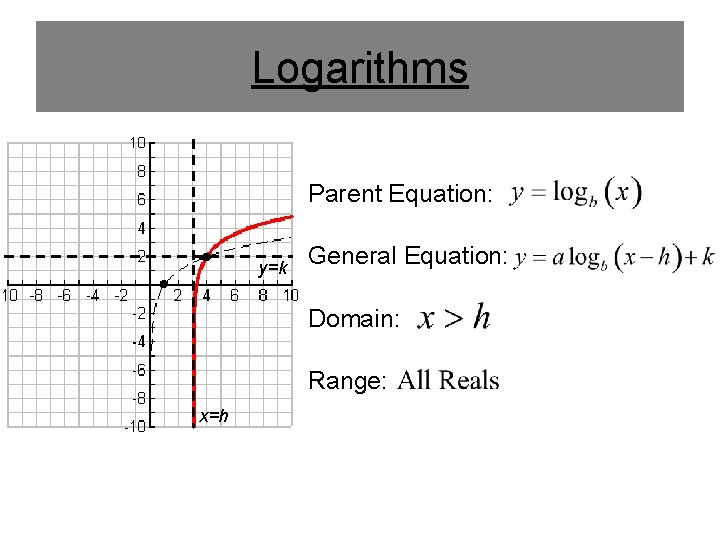
Logarithms Parent Equation: y=k General Equation: Domain: Range: x=h

Day 44: November 9 th Objective: Assess chapter 6 in a team setting. • Homework Check • Chapter 6 Team Test • Closure Homework: 6 -113 to 6 -120 (pgs 294 -295)

Day 45: November 10 th Objective: Assess Chapters 1 -5 in a individual setting. • Homework Check • Midterm Exam • Closure Homework: 7 -9 to 7 -15 (pgs 309 -310)