VERTEX Form of Quadratic Functions Math 2 Y

VERTEX Form of Quadratic Functions Math 2 Y

Vertex Form: • h moves the parabola horizontally • k moves the parabola vertically • a makes the parabola narrow or wide • VERTEX => (opposite h, k) • Axis of Symmetry is x = opposite h *Reminder* If a > 0 (positive), parabola opens up If a < 0 (negative), parabola opens down

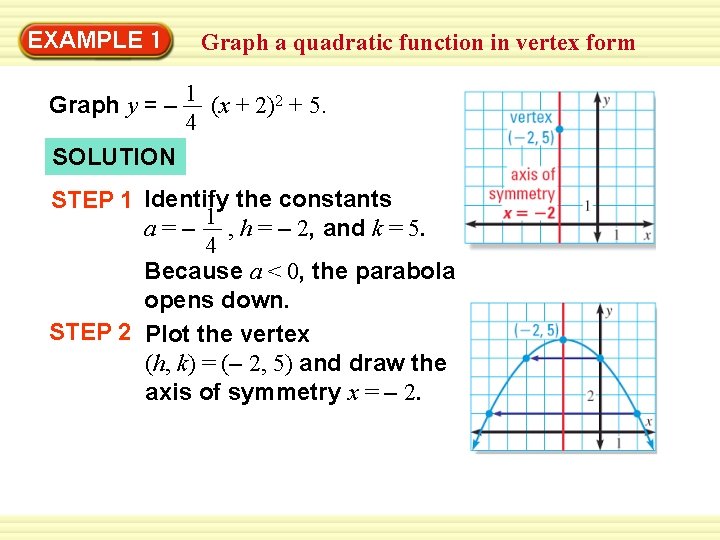
EXAMPLE 1 Graph a quadratic function in vertex form Graph y = – 1 (x + 2)2 + 5. 4 SOLUTION STEP 1 Identify the constants a = – 1 , h = – 2, and k = 5. 4 Because a < 0, the parabola opens down. STEP 2 Plot the vertex (h, k) = (– 2, 5) and draw the axis of symmetry x = – 2.

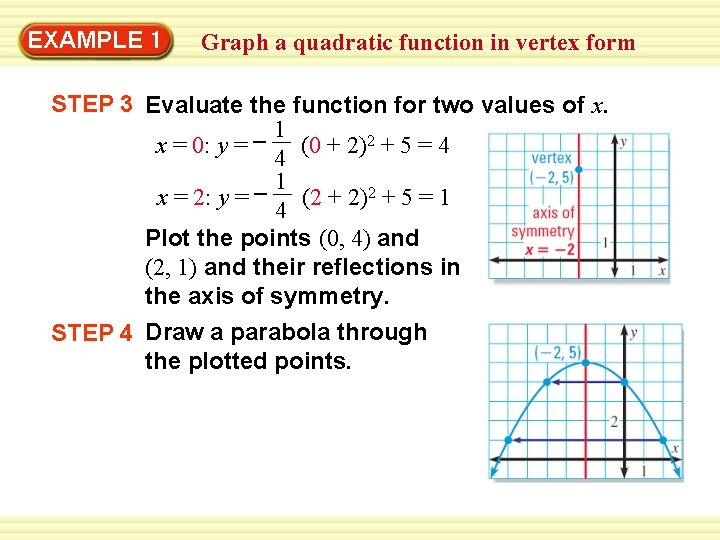
EXAMPLE 1 Graph a quadratic function in vertex form STEP 3 Evaluate the function for two values of x. 1 – x = 0: y = (0 + 2)2 + 5 = 4 4 1 – x = 2: y = (2 + 2)2 + 5 = 1 4 Plot the points (0, 4) and (2, 1) and their reflections in the axis of symmetry. STEP 4 Draw a parabola through the plotted points.

GUIDED PRACTICE Graph the function. Label the vertex and axis of symmetry. 1. y = (x + 2)2 – 3 h= k= Vertex: ( ___ , ___ ) a= Axis of symmetry: x =

GUIDED PRACTICE 2. y = –(x + 1)2 + 5 h= k= Vertex: ( ___ , ___ ) a= Axis of symmetry: x =

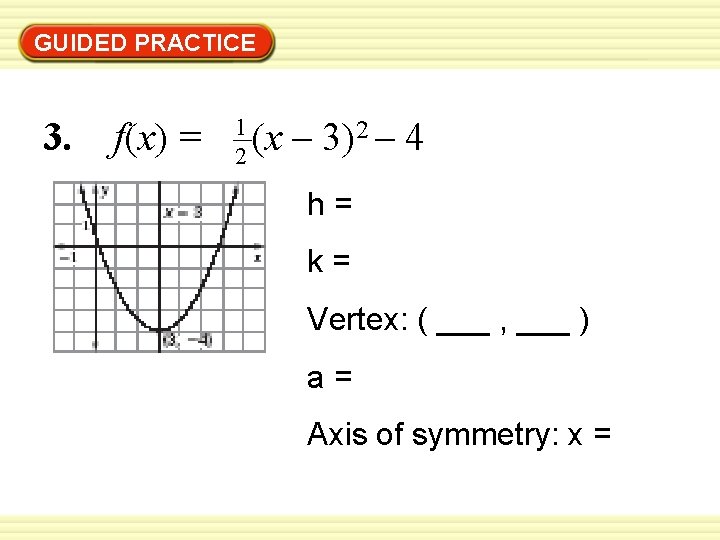
GUIDED PRACTICE 3. f(x) = 1 2 (x – 3)2 – 4 h= k= Vertex: ( ___ , ___ ) a= Axis of symmetry: x =

Writing in Standard Form • Goal is to manipulate the numbers so that they are in the form f(x) = ax² + bx + c *Reminder* Order of Operations: PEMDAS!! • You will need to distribute monomials, binomials, and trinomials! • Let’s look at some examples…

EXAMPLE 3 Change from intercept form to standard form Write y = – 2(x + 5)(x – 8) in standard form. y= = – 2(x + 5)(x – 8) – 2(x 2 – 8 x + 5 x – 40) – 2(x 2 – 3 x – 40) – 2 x 2 + 6 x + 80 Write original function. Multiply by Distributing. Combine like terms. Distributive property

EXAMPLE 3 Change from vertex form to standard form Write f (x) = 4(x – 1)2 + 9 in standard form. f (x) = = = 4(x – 1)2 + 9 4(x – 1) + 9 4(x 2 – x + 1) + 9 4(x 2 – 2 x + 1) + 9 4 x 2 – 8 x + 4 + 9 4 x 2 – 8 x + 13 Write original function. Rewrite (x – 1)2. Multiply by Distributing. Combine like terms. Distributive property Combine like terms.

GUIDED PRACTICE Write the quadratic function in standard form. 7. y = –(x – 2)(x – 7) ANSWER –x 2 + 9 x – 14 8. y = – 4(x – 1)(x + 3) ANSWER – 4 x 2 – 8 x + 12

GUIDED PRACTICE Write the quadratic function in standard form. 9. y = – 3(x + 5)2 – 1 ANSWER – 3 x 2 – 30 x – 76 10. g(x) = 6(x – 4)2 – 10 ANSWER 6 x 2 – 48 x + 86

GUIDED PRACTICE Graph the function. Label the vertex, axis of symmetry, and zeros. 4. y = (x – 3)(x – 7) Zeros: Vertex: ( ___ , ___ ) Axis of symmetry: x =

GUIDED PRACTICE 5. f (x) = 2(x – 4)(x + 1) Zeros: Vertex: ( ___ , ___ ) Axis of symmetry: x =

Assignment => Textbook pg. 67 # 2 -14 even, 20, 22, 28, 30 (You will be given 6 blank graphs for #12, 14, 20, 22)