VERLERN SINIFLANDIRILMASI VE GRAFKLER Belli bir aratrma sonunda

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Belli bir araştırma sonunda elde edilen ham verilerin tablo haline getirilmesine frekans tablosu adı verilir. Frekans tablosu, sınıf limitleri ve frekanslara ait sütunlardan oluşan bir tablodur. Frekans tablosunda bunun haricinde başka sütunlarda (sınıf sınırı, sınıf değeri, den az, den çok eklemeli frekanslar v. b. ) yer alır. Ancak bu özellikler frekans tablosunu oluşturmazlar. Bunlar daha ziyade çeşitli istatistiklerin hesaplanmasında kullanılır.

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER 1) Sürekli Verilerin Sınıflandırılması Bu tip verilere ait frekans tablosunun oluşturulmasında aşağıdaki yol izlenir. a) Veriler küçükten büyüğe doğru sıralanır. Ancak bu durum keyfidir, sıralama yapılmasa da olur. b) Sınıf sayısına karar verilir. c) 1. sınıfın alt limit değeri öyle seçilmelidir ki ham verilerin içerisindeki en küçük değer, 1. sınıfın alt ve üst sınıf limitleri arasında yer alsın. d) Son sınıfın üst limit değeri öyle seçilmelidir ki ham verilerin içerisindeki en büyük değer, son sınıfın alt ve üst sınıf limitleri arasında yer alsın.

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER e) Sınıf aralığı aşağıdaki formülden hesaplanır. f) Sınıf aralığı hesaplandığında, virgülden sonraki 5 ve daha yukarı haneler için bir üste tamamlanır, 5’in altındaki değerler için ise bir alt değer alınır.

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Örnek: Bir grup öğrencinin genel yetenek testinden aldığı puanlar aşağıdaki gibidir: 25, 31, 44, 26, 32, 63, 56, 38, 47, 45, 73, 72, 74, 76, 73, 61, 34, 27, 48, 51, 57, 44, 42, 41 birinci sınıfın alt limiti 25 olmak üzere 9 sınıflı bir frekans tablosu düzenleyiniz. Sınıf Aralığı

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Sınıflar fi 25 -30 3 31 -36 3 37 -42 3 43 -48 5 49 -54 1 55 -60 2 61 -66 2 67 -72 1 73 -78 +4 24 Yapılan frekans tablosuna bazı eklemeler yapmak mümkündür. Ancak yapılan bu eklemeler, frekans tablosu olarak adlandırılamaz. Bunlar daha önceden de izah edildiği gibi bazı istatistiklerin hesaplanmasında ve grafiklerin çizilmesinde yardımcı olan bilgilerdir. Şimdi bu ek sütunların oluşturulması aynı örnek üzerinde izah edilecektir.

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Sınıf Sınırı : Sınıf sınırı hesaplanırken önce 1. sınıfın alt sınıf limiti ile (25), 2. sınıfın üst sınıf limitinin (36) ortalaması alınır, bu değer 1. sınıfın üst sınıf sınırı olarak yazılır. Bu değerden sınıf aralığı (6) çıkarılarak 1. sınıfın alt sınıf sınırı bulunur. En son işlem 1. sınıfın alt ve üst sınıf sınırlarına sınıf aralığı eklenerek diğer sınıfların sınıf sınırları bulunmuş olur. Sınıf sınırları 24. 5 -30. 5 -36. 5 -42. 5 -48. 5 -54. 5 -60. 5 -66. 5 -72. 5 -78. 5

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Sınıf değeri(Xi) : 1. sınıfın alt ve üst limit değerlerinin ortalaması alınarak, 1. sınıfın sınıf değeri bulunur. Bu değere sınıf aralığı eklenerek diğer sınıfların sınıf değeri bulunmuş olur. Xi 27. 5 33. 5 39. 5 45. 5 51. 5 57. 5 63. 5 69. 5 75. 5

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Nisbi frekans (Ni) : Nisbi frekans aşağıdaki eşitlikten hesaplanır: Yüzde frekans (Yi): Yüzde frekans aşağıdaki formülden hesaplanır: Yi (%) = Ni. 100 Buna göre aynı şekilde nisbi ve yüzde frekanslar

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Ni Yi (%) 0. 125 12. 5 0. 2083 20. 83 0. 0417 4. 17 0. 0833 8. 33 0. 0417 4. 17 +0. 1667 +16. 67 1. 0000 100. 00 Örnekte görüldüğü gibi nisbi frekanslar toplamı daima 1, yüzde frekanslar toplamı da daima 100’dür.

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Eklemeli (Yığmalı) Frekanslar Bu tip frekanslar -den daha az ve -den daha çok şeklinde frekanslar olup, belli bir sınıf sınırından az veya belli bir sınıf sınırından çok frekansları ifade etmek için kullanılır. -den az ve -den çok eklemeli frekanslar oluşturulurken den az da üst sınıf sınırları kriter alınır ve frekanslar toplanarak diğerleri bulunur, -den çok eklemeli frekanslar için ise alt sınıf sınırları kriter alınır, 1. sınıfın -den çok eklemeli frekansı toplam frekanstır; bu frekanstan diğer sınıfların frekansları çıkarılarak diğer sınıfların -den çok eklemeli frekansları bulunur.

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Sürekli Verilere Ait Frekans Tablosu Sınıflar fi Xi Sınıf (sınıf değ) sınırları -den az -den çok Ni Yi (%) 25 -30 3 27. 5 24. 5 -30. 5 3 24 0. 125 12. 5 31 -36 3 33. 5 30. 5 -36. 5 6 21 0. 125 12. 5 37 -42 3 39. 5 36. 5 -42. 5 9 18 0. 125 12. 5 43 -48 5 45. 5 42. 5 -48. 5 14 15 0. 2083 20. 83 49 -54 1 51. 5 48. 5 -54. 5 15 10 0. 0417 4. 17 55 -60 2 57. 5 54. 5 -60. 5 17 9 0. 0833 8. 33 61 -66 2 63. 5 60. 5 -66. 5 19 7 0. 0833 8. 33 67 -72 1 69. 5 66. 5 -72. 5 20 5 0. 0417 4. 17 73 -78 4 75. 5 72. 5 -78. 5 24 4 0. 1667 16. 67 24 1. 0000 100. 00

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER 2)Kesikli Verilerin Sınıflandırılması Kesikli veriler, 1. Bölümde tanımlandığı gibi saymak sureti ile elde edilen verilerdir. Bu tip verilerde sınıflar arasında bir süreklilik olmadığı için, bu tip verilere ait frekans tablosunda sınıflar, sınıf sayısı ve sınıf değerleri otomatik olarak bellidir. Örnek : 30 günlük periyot içerisinde köyden şehre otobüsle seyahat eden insanların sayısı aşağıdaki gibidir. 6, 3, 2, 7, 4, 0, 5, 1, 3, 2, 6, 2, 4, 4, 3, 0, 5, 2, 1, 2, 4, 3, 5, 2, 4, 6, 3, 0, 7, 1 Bu verilere ait frekans tablosu aşağıdaki şekilde oluşturulur. Verilerin içerisinde en küçük değer 0 ve en büyük değer 7’dir. O halde sınıflar 0 ile 7 arasında değişecektir.

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Kesikli verilerin frekans tablosu Sınıflar fi Ni Yi (%) 0 3 0. 10 10 1 3 0. 10 10 2 6 0. 20 20 3 5 0. 17 17 4 5 0. 17 17 5 3 0. 10 10 6 3 0. 10 10 7 2 0. 07 7 30 1. 00 100

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Sürekli Verilere Ait Grafikler Sürekli veriler ya histogram grafiğinde yada frekans poligon grafiğinde gösterilirler. Histogram grafiği, X ekseninde sınıf sınırlarının Y ekseninde ise frekansların yer aldığı bir grafikten oluşur. Frekans poligonu ise X ekseninde sınıf değerlerinin Y ekseninde frekansların kesiştiği noktalardan oluşur. Verilen örnekte histogram grafiği ve frekans poligonunun çizimi aşağıdaki gibidir.

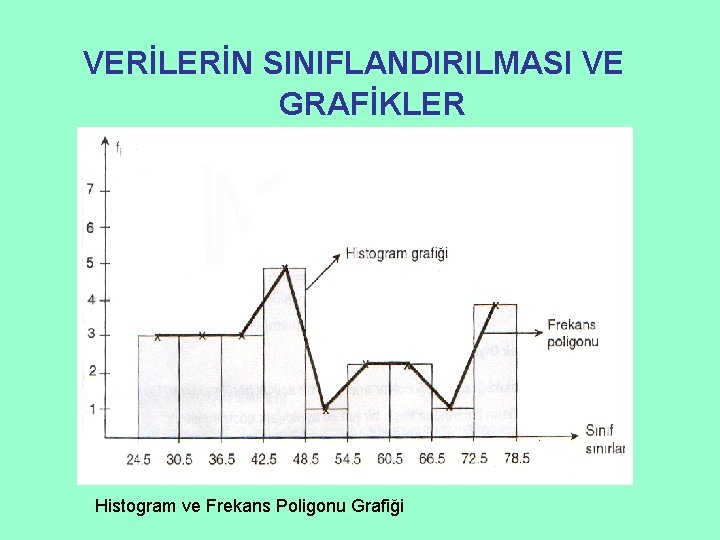
VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Histogram ve Frekans Poligonu Grafiği

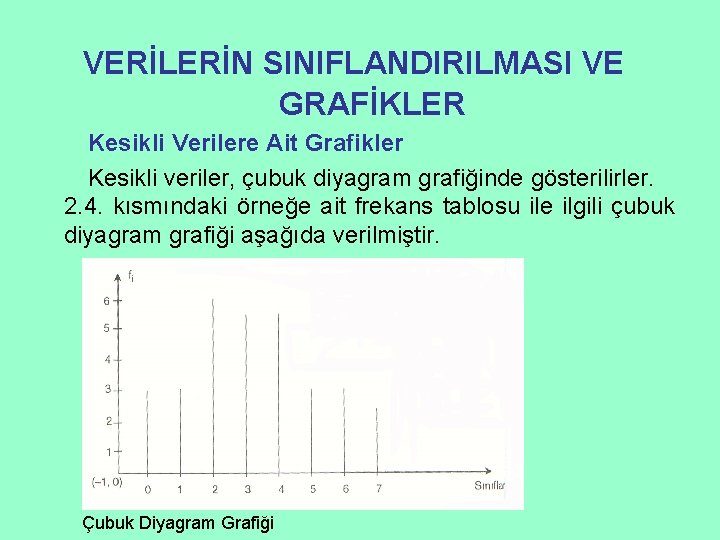
VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Kesikli Verilere Ait Grafikler Kesikli veriler, çubuk diyagram grafiğinde gösterilirler. 2. 4. kısmındaki örneğe ait frekans tablosu ile ilgili çubuk diyagram grafiği aşağıda verilmiştir. Çubuk Diyagram Grafiği

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER Eklemeli (Yığmalı) Frekanslara Ait Grafikler Bu tip grafikler çizilirken X ekseninde sınıf sınırları, Y ekseninde ise eklemeli frekanslar yer alır. Bu noktaların kesiştiği yerler birleştirilerek -den az ve -den çok eklemeli frekans grafiği elde edilir. -den az eklemeli frekans eğrisi artan bir fonksiyondur, diğeri ise azalan bir fonksiyondur. Buna göre, eklemeli frekans grafiği,

VERİLERİN SINIFLANDIRILMASI VE GRAFİKLER